Map
HTML
-
自20世纪末啁啾脉冲放大技术被发明以来，众多学者已经对高能激光和物质的相互作用展开了相关研究[1-3]，尤其是在超快激光物理领域[4-6]。相对论强度激光束中的光子与高能电子相互作用，产生汤姆逊散射，由于多普勒频移的存在，此过程为非线性过程。非线性汤姆逊散射过程是获得X射线[7]和γ射线[8-9]的方式之一, 同时也是广泛应用于生物医药领域[10-11]的单色激光[12-13]和超短阿秒激光[14-15]的重要辐射源。在观测超快无规律物理过程, 如原子物理及核物理过程[16-17]中也有着诸多应用。
在汤姆逊散射过程中，入射激光的不同参数对电子的空间运动轨迹和辐射特性有着不同影响。高能激光场中的运动电子在有质动力下被加速，在洛伦兹力的作用下发生垂直方向的转向。不同初始状态下的电子与不同的激光辐射作用后显示出不同的空间和时间特性。
多年以来，学者们对相对论条件下的非线性汤姆逊散射过程提出过许多疑问[18-19]。LEE等人对不同偏振态的强激光与静止单电子相互作用的汤姆逊散射过程进行计算机仿真模拟，研究了该过程下的谐波结构的特性，发现了光谱的调制结构[20]。在LEE的研究基础上，ZHENG等人研究了初始静止电子的辐射能量角分布规律[21]。VAIS分析了线偏振汤姆逊散射的辐射能量、光谱和角分布，并对散射辐射与测试电子初始位置之间的关系进行了进一步探讨[22]。LI等人以入射光强为变量，提出线偏振激光下的空间辐射呈双叶状[23]。WANG等人将圆偏振紧聚焦激光与位于原点的静止电子之间的相互作用作为研究对象，总结出辐射角分布与3维电子轨迹之间的关系[24]。BAUER和CHEN等人基于有质动力理论研究了激光强度对电子轨迹和电子辐射特性的影响[25-26]。
在紧聚焦圆偏振激光与相反方向运动的电子对撞条件下，作者以不同对撞中心下电子的空间轨迹和辐射能量特性为研究对象, 通过对3维和2维图像的分析，数值模拟结果显示，对撞中心距离光焦点越近，电子运动轨迹的振幅越大。由于有质动力的影响，电子运动轨迹振幅在坐标原点附近呈现出非对称性。同时发现了最大辐射功率对应的极角θ为恒定值，并且阐述了方位角ϕ的变化规律。此外，发现电子辐射时间谱的非对称性，也就是辐射脉冲呈现主峰和次峰现象，并对峰值变化进行研究和讨论。
-
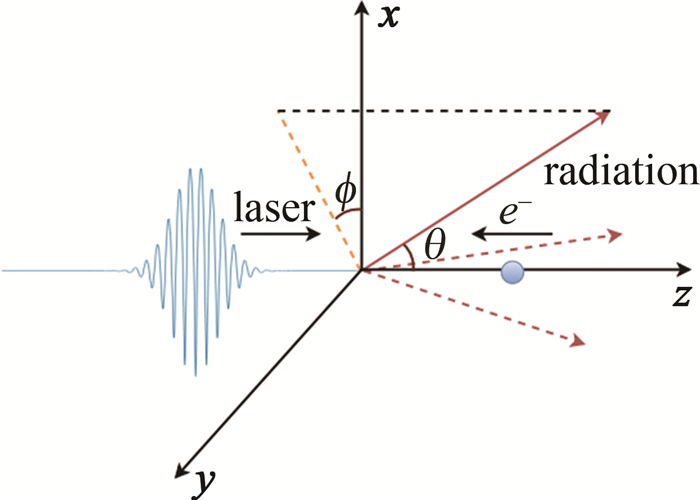
如图 1所示，沿着参考系的+z轴方向引入一束入射角σin=0°的圆偏振激光脉冲，激光场的矢势a可以表示为如下形式[19]：
Figure 1. Schematic diagram of laser and electron collision movement and radiation
式中, δ为偏振参数; A为不考虑偏振态的激光矢势复数形式; u(ρ, z)用于描述辐射分布情况; a0是被mc2/e归一化的激光振幅，m和e分别为电子静止质量和净电荷, c为光速; L和w分别表示激光脉宽和光斑半径，w与激光前进位置z的值有关; R为激光的曲率半径; w=w0(1+z2zR2)1/2，w0为z=0点的激光束腰半径; zR=w02为瑞利长度; ρ2=x2+y2，η=z-t，t为观测时间。考虑库伦规范$\nabla $·a=0，矢势可以被进一步分解为以下正交分量形式[24]：
其中，
激光相位φ可以表达为如下形式：
式中, φ0为初相位，φR=(x2+y2)(1+zR2z2)为与波前曲率相关的相位, φG=z/zR为与瑞利长度相关的古依相移。在这个模型中，空间和时间被波数k0-1和激光频率ω0-1分别归一化。
-
引入一束沿+z轴方向前进的激光脉冲，具有动量p=γu的高能电子沿着-z轴方向前进，此处p被mc归一化，γ=(1-u2)-1/2为相对论因子。电子在电磁场中的轨迹可以用如下拉格朗日方程和能量方程来描述[27]：
式中，$\frac{\mathrm{d} \gamma}{\mathrm{d} t}=\boldsymbol{u} \cdot \frac{\partial \boldsymbol{a}}{\partial t}$，电子速度u被光速c归一化。根据以下方程, 结合(4)式~(5)式可以计算电子任意时刻的速度(ux，uy，uz)，加速度和位置(ax，ay，az):
式中，px，py，pz为电子动量的3个分量。此外，电子在激光场中的运动状态也被有质动力${\mathit{\boldsymbol{F}}_{\rm{p}}} = - m{c^2}\nabla (1 + {\left. {{\mathit{\boldsymbol{p}}^2}} \right)^{1/2}}$所影响。其中$\nabla$为哈密顿算子。
-
相对论速度下的电子会释放电磁辐射，在笛卡尔坐标系中，电子辐射方向可用如下方程表示：
式中, θ规定了激光前进的方向，ϕ表示垂直于对撞方向的平面方位角。在t时刻，单位立体角的辐射功率可以如下表示[27]：
式中，s0是观察点与对撞中心之间的距离，r为电子位置矢量, 辐射功率被e2ω02/(4πc)归一化。考虑观测点和对撞区域之间的距离，令t′为碰撞发生的时间，t为观测时间。
1.1. 圆偏振高斯激光
1.2. 激光场中的电子轨迹
1.3. 空间辐射的角分布
-
下述圆偏振高斯激光沿着z轴传播，光强参数a0=6.0，达到相对论光强，波长λ0=1μm，束腰半径w0=3λ0，脉宽L=3λ0。此外洛伦兹因子γ0=20的电子，沿着高斯激光相反方向运动。
借助上述理论模型及计算机程序，得到激光场中电子轨迹和辐射功率的模拟结果。通过对不同对撞中心的数值结果和理论图像分析，发现并解释了紧聚焦激光脉冲与高能电子对撞后电子轨迹的非对称性，探讨了对撞中心对电子辐射和时间谱的影响。
-
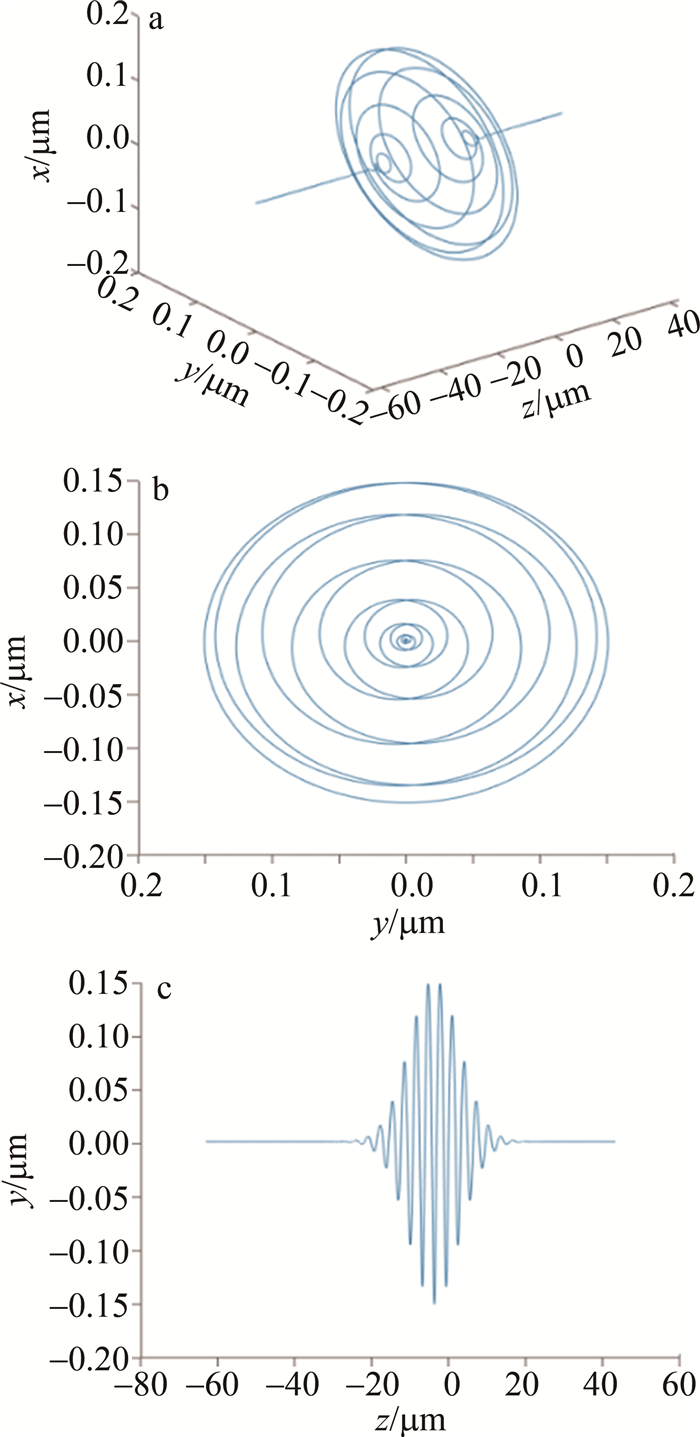
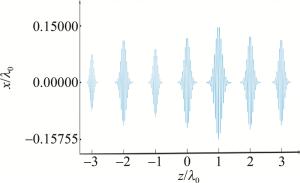
通过对笛卡尔坐标系中电子轨迹的分析，发现电子轨迹呈现出中间宽两头缩为一点的螺旋状。从图 2中可以看出，电子轨迹沿着yOz平面呈现出非对称性。电子轨迹距离z轴最远的一点到z轴的距离称作电子轨迹振幅，图 3中5个位置分别是对撞中心位于-λ0，0，λ0，2λ0，3λ0的xOz平面轨迹。从图中可以看到，随着对撞中心与激光聚焦点的距离的减小，电子轨迹振幅增大。若将高斯激光聚焦位置作为对称轴，左侧(z < 0)的电子轨迹振幅总是小于右侧(z>0)电子轨迹振幅。且在-λ0处，电子轨迹振幅骤然减小，达到了最小值。在λ0处，电子轨迹振幅达到了峰值。
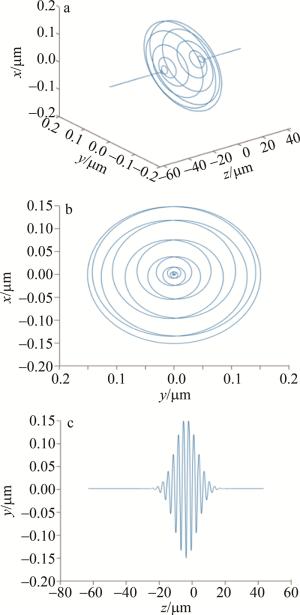
Figure 2. a—schematic diagram of the trajectory of the electronic movement b—projection of the electronic trajectory on the xOy plane c—projection of the electronic trajectory on the yOz plane
Figure 3. Electron trajectories of different collision centers (2-D)
以上现象可以通过电子在激光场中运动所受到的电场力和有质动力的共同作用进行解释。从图 3中可知，在靠近激光聚焦点的地方，激光强度最大，在焦点处聚焦性最强。由第1.2节中的公式可见，激光势能越大，电子速度越快，轨迹振幅越大。因此，随着对撞中心处激光强度不断增强，电子轨迹的振幅也随之增大。这就解释了图 3中电子轨迹振幅先增大后减小的现象。
有质动力对激光场中运动的电子的影响也是不容忽视的。结合图 4和(11)式可知，在平行于z轴方向，有质动力施加与电子运动方向相反的力；在垂直于z轴方向，有质动力对电子运动的影响分成两种情况进行讨论：(1)当激光的电场方向与电子运动方向相同时，有质动力对电子起到垂直方向的加速作用; (2)当激光的电场方向与电子运动方向相反时，有质动力对电子的垂直方向起减速作用。
当对撞中心在-λ0时，电子垂直于z轴方向的运动受到有质动力的阻碍，因此振幅不断减小; 在λ0时，有质动力与电子垂直方向相反，对电子的运动具有加速作用，因此振幅不断增大。
-
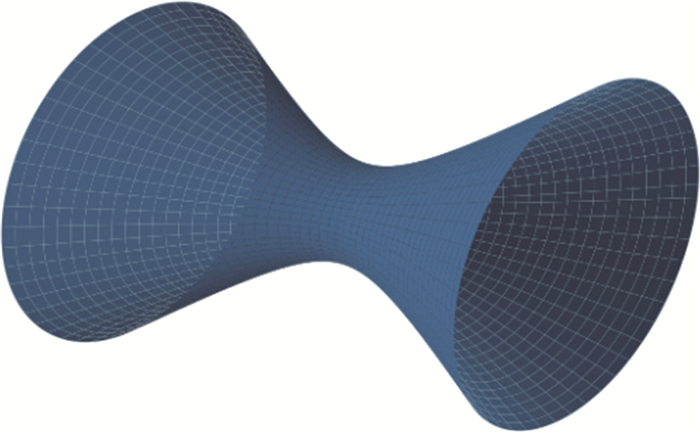
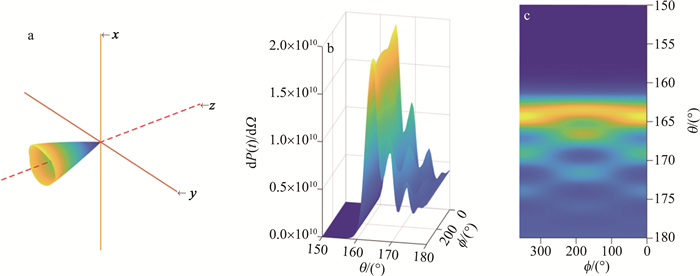
由图 5可见，电子辐射分布总体呈圆锥体形。图 5中颜色的连续变化表明空间中电子辐射的连续性。在进一步的研究中，以ϕ, θ, dP(t)为自变量将圆锥体形电子轨迹图像转化为易于分析的3-D图像，并且得到更多电子辐射特性，尤其是对撞中心对电子辐射分布角度θ和ϕ的影响。
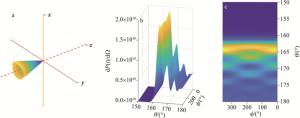
Figure 5. a—electron radiation complete 3-D space radiation b, c—expanded diagram of electron radiation based on spherical coordinates
通过对表 1中数据的分析可以看出，随着对撞中心位置的改变，极角θ的值维持在164.5°不变，ϕ随着对撞中心的变化发生连续变化，从球坐标系角度，随着对撞中心的连续变化，辐射功率的角分布图像绕激光前进方向的轴连续“旋转”。其中ϕ的值与对撞时激光的相位有关。随着对撞中心位置的改变，对撞中心处激光相位也发生相应的改变，由此导致了方位角ϕ的变化。
position/λ0 θ/(°) ϕ/(°) -3 164.5 359 -2 164.5 359 -1 164.5 0 0 164.5 0 1 164.5 1 2 164.5 1 Table 1. Azimuth and polar angle of electron radiation at different collision centers
-
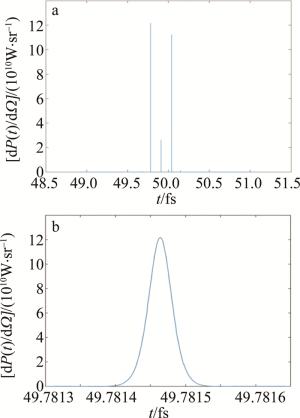
在不同对撞中心下，对电子辐射时间谱进行探究，如图 6所示。与先前的认知不同的是，电子辐射时间谱呈现出非对称的双峰状，也就是主峰与次峰现象，主峰强度(非归一化处理)达到1.21764×1011W/sr，在主峰和次峰之间存在着更小峰值的峰，这与先前发现的正三角形完全不同。改变对撞中心位置并且对主峰峰值进行记录，随着对撞中心向z轴的正半轴进行移动，主峰峰值的大小呈下降趋势。
Figure 6. a—time history of the radiated power per solid angle in the direction of maximum radiation b—a magnified version of the peak radiation
2.1. 电子轨迹
2.2. 电子辐射角
2.3. 电子辐射时间谱
-
探究了对撞中心位置对高能电子轨迹和辐射特性的影响，研究表明，越靠近高斯激光的焦点，电子轨迹振幅越大。在有质动力的影响下，电子轨迹的振幅变化曲线呈现非对称性。随着对撞中心的变化，最大电子辐射对应的极角θ保持在164.5°不变，方位角ϕ则呈现周期性变化。在3λ0处，电子辐射功率达到峰值。电子辐射脉冲呈现出主峰和次峰的非对称性，峰的大小随着对撞中心与激光焦点距离的增大而增大。
本文中的研究同时也有望作为未来电子辐射(例如X射线)的产生应用的理论准备。
DownLoad: