HTML
-
近几十年来, 激光光束聚焦中出现的焦移和焦开关现象得到广泛研究[1-12]。而近年来对这些现象的研究已经延伸到微纳米领域[13-18]。2012年,GAO等人研究了2维金属纳米缝透镜中的焦移现象,指出光束的相对焦移只依赖于菲涅耳数,而菲涅耳数受透镜尺寸、焦距、入射光波长3个因素影响,发现菲涅耳数为0.63时光束的相对焦移达到48.9%[14]。HE等人在2015年对基于GaN高对比度光栅的2维透镜中的焦移进行了研究,分析了器件缝宽度、透镜焦距长度、相位差等参量对光束焦移的影响,计算所得数据显示当菲涅耳数为0.8时光束的相对焦移接近50% [15]。2018年,JIA等人研究了正方形超透镜中的焦移,并用时域有限差分法(finite-difference time-domain,FDTD)方法进行了仿真,研究中的仿真结果与理论分析结果有很好的一致性[18]。
近年来,作者所在团队一直在探索光束的焦移和焦开关现象,在研究中得到了一些新的结果。本文中研究了宽带TEM22模厄米-高斯(Hermite-Gaussian, HG)光束通过受光阑限制色散会聚透镜的微米焦开关现象。首先得到了宽带TEM22模HG光束通过受光阑限制色散会聚透镜的传输表示式,然后通过数值计算详细分析光束的带宽和菲涅耳数对TEM22模HG光束微米焦开关现象的影响,最后对文中的研究结果进行了总结。
-
对于受光阑限制的色散会聚透镜系统,其传输矩阵为:
式中,A, B, C, D分别为传输矩阵的矩阵元,z为研究的考察面到初始入射面的距离,f(λ)为与波长λ相关的色散透镜焦距,且f(λ)=(n0-1)f0/[n(λ)-1],n0为中心波长λ0对应的折射率,f0为λ0对应的焦距,n(λ)为对应波长λ的折射率。考虑色散透镜的材料为熔融石英,则其折射率n(λ)由参考文献[19]中给出。当宽带TEM22模HG光束通过这一系统后,对于光束的每一频率分量,考察面z处的场分布为:
式中,E22(x0, y0, 0, ω)是初始入射面的场分布,a是正方形硬边光阑中心孔的半宽,k=2π/λ, 为波数,x和y为考察面坐标,ω为频率。
为简单起见,考虑初始入射面z=0处的空间分量E22(x0, y0, 0)和频谱分量f(ω)可分离,即E22(x0, y0, 0, ω)=E22(x0, y0, 0)f(ω),且:
式中,H2()为厄米多项式,w0为对应的基模高斯光束束腰宽度,并且1/q0=-iλ/(πw02),q0为z=0处的q参量。假设f(ω)为典型的高斯型,即:
式中,γ=Δω/ω0为相对带宽,Δω为带宽,ω0为中心频率,aG=(2ln2)1/2。
光束通过透镜后,由傅里叶逆变换,可以得到任一点处在时间域的场分布为:
式中,时间t=z/c,c是光速。为推导和计算的方便,仅考虑TEM22模HG光束的1维情况,2维情况下的结果是类似的。因此,积分得到TEM22模HG光束1维场分布为:
式中,${T = 1 - \frac{{{\rm{i \mathsf{ π} }}{F_{\rm{w}}}[z - f(\lambda )]/f(\lambda )}}{{z/f(\lambda )}}}$,${Q = \frac{{{\rm{i \mathsf{ π} }}{F_{\rm{w}}}}}{{{T^{1/2}}z/f(\lambda )}}}$,${S = \frac{{{\rm{i}}{F_{\rm{w}}}}}{{z/f(\lambda )}}\exp \left\{ {\left[ {{Q^2} - \frac{{{\rm{i \mathsf{ π} }}{F_{\rm{w}}}}}{{z/f(\lambda )}}} \right]{{\left( {\frac{x}{{{w_0}}}} \right)}^2}} \right\}}$,${\left. {{W_x} = {\mathop{\rm erf}\nolimits} (\sqrt {\alpha T} - Qx/{w_0}} \right) + {\mathop{\rm erf}\nolimits} \left( {\sqrt {\alpha T} + Qx/{w_0}} \right)}$。另有α=(a/w0)2和Fw=w02/分别是截断参量和光束相关的菲涅耳数,erf()是误差函数。最后得到TEM22模HG光束通过色散透镜的1维场分布:
光强分布则为I22(x, z, t)=E22(x, z, t)2。
-
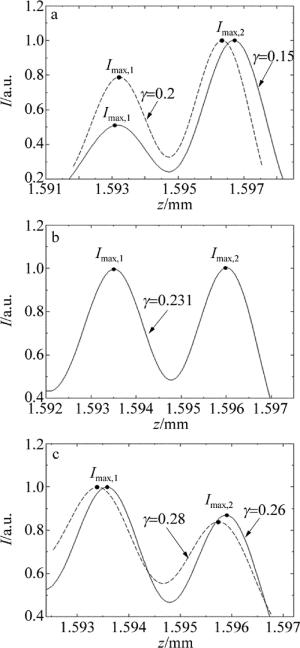
接下来给出了TEM22模HG光束光强分布的数值计算示例。计算参量为中心波长λ0=800nm,对应焦距f0=1.6mm,截断参量α=4。本文中主要关心的是TEM22模HG光束光强极大变化情况,因此以下计算结果都是t=z/c时的光强分布。图 1是γ为0.15, 0.2, 0.231, 0.26, 0.28, 且Fw=100时TEM22模HG光束的轴上光强I分布和两个光强极大Imax, 1和Imax, 2的变化。当γ为0.15, 0.2时,Imax,2比Imax,1大,Imax,2是光强主极大,但随着γ增大,Imax, 2减小而Imax, 1增大;当γ=0.231时,二者相等; 当γ为0.26, 0.82时,Imax, 1比Imax, 2大,Imax, 1是光强主极大。图中结果表明,在γ=0.231时, TEM22模HG光束的光强主极大位置迅速跃迁,出现了类似参考文献[1, 3, 5, 8-9, 12]中的焦开关现象。与已有的研究结果相比较,本文中的结果说明在高阶高斯光束中也存在带宽变化引起的焦开关现象。
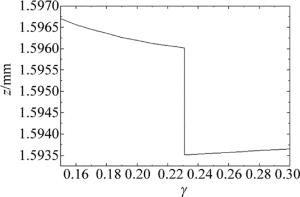
图 2是光强主极大位置随γ的变化。当γ < 0.231时,光强主极大位于1.5960mm和1.5967mm之间, 随着γ增大其位置远离几何焦点。然而当γ>0.231,光强主极大位于1.5935mm和1.5937mm之间, 随γ增大其位置朝向色散会聚透镜的几何焦点移动。从结果看出,光强主极大位置不但随γ发生变化,而且在γ不同区域变化趋势不一样。另外,在γ=0.231,光强主极大位置从1.5960mm跃变到1.5935mm,跃变距离2.5μm。即本文中TEM22模HG光束出现的焦开关现象是微米量级的焦开关。这种微米焦开关现象对于微米光学器件的设计和制作有一定的意义。
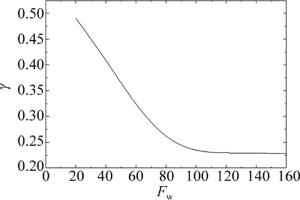
数值计算结果还表明,TEM22模HG光束微米焦开关现象并不仅仅只是在γ=0.231时出现,即带宽不是唯一的影响因素。当Fw=60时,焦开关现象将不在γ=0.231时出现,而是在γ=0.325时出现。图 3中给出了诱导焦开关出现的相对带宽随菲涅耳数变化。图中结果表明, 当菲涅耳数较大时,TEM22模HG光束较小的带宽就可以诱导焦开关出现。而菲涅耳数较小时,TEM22模HG光束则需要较大的带宽才能诱导焦开关现象。特别是当菲涅耳数小于80时,带宽迅速增大。例如,Fw约大于110时,γ≈0.23并保持一个固定值,而当Fw=20时, 需要γ≈0.5才能诱导焦开关出现。
-
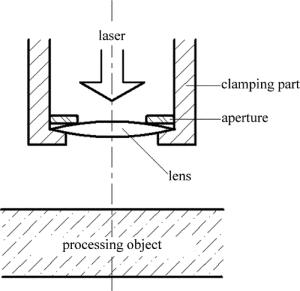
设计了一种采用TEM22模HG光束对微米光学器件进行加工制作的激光微加工系统,系统结构示意图如图 4所示。该系统可能完成两种不同情况的加工。一是由于激光束两个光强极大可以发生相对变化,对微米光学器件中相距微米量级的不同部位进行加工时,改变光束参量即可实现,无需移动激光头和被加工物体。二是由于激光束可以有两个相同大小的光强极大,因此可以对器件内相距微米量级的两个部位同时进行加工,与通常情况下只有一个光强极大的激光束相比效率提高1倍。这样可以提高加工精度和加工效率。
-
本文中研究了TEM22模HG光束通过色散会聚透镜的光强分布和微米焦开关现象。当TEM22模HG光束通过色散会聚透镜系统,带宽的变化导致TEM22模HG光束的光强分布中出现彼此竞争的两个光强极大,二者的此消彼长诱导了焦开关出现。当γ=0.231且Fw=100时, 光强主极大位置从1.5960mm跃变到1.5935mm,跃变距离2.5μm,表现为微米量级的焦开关现象。研究结果还表明,诱导焦开关出现的TEM22模HG光束带宽还随菲涅耳数变化。微米焦开关现象可用于微纳光学领域的光束调控,有助于光通信技术中微纳光学器件的设计和制作。

 Map
Map




 DownLoad:
DownLoad:


