Light bar centerline extraction method based on density clustering

光学测量技术与计算机技术的发展，使得非接触3维测量技术得到广泛应用，这对测量精度和实时性提出了新的挑战^[1-2]。基于线结构光的单目3维测量在大多数测量环境中经过适当调整均可达到较高精度, 系统制造费用低，且可以满足在线测量的需求，因此被广泛用于各种工业测量场景^[3]。其中，物体表面激光中心线的提取对测量精度产生了至关重要的影响。

在各种中心线提取算法中，阈值法^[4]、极值法^[5]等受图像噪声影响大，曲线拟合法^[6]受影响较小, 但时间复杂度偏高。基于Hessian矩阵的Steger方法^[7]进一步提高了对噪声的鲁棒性，但由于需要对图像中各像素点进行多次卷积操作，算法复杂度高，加之需要良好的图像预处理手段，因而不能满足实时性的需要。灰度重心法^[8]是一种常用的激光中心线提取方法，该方法利用光条灰度值呈高斯分布的特点对中心进行计算，并结合阈值选取过程对低亮度图像噪声进行剔除，算法使用线性计算，因而时间复杂度低，但该法仅适用于光条灰度满足高斯分布、宽度一致性高、分布较为集中的场景^[9]。

在实际工业测量中，受激光发生器的制造误差以及物体表面形貌影响，激光光条不能满足理想高斯分布，另外，受图像采集设备缺陷、环境光照射不均、被测物体表面复杂且反射率不同等因素影响，采集到的原始图像同时含有激光光条和噪声光斑，光斑具有随机分布、亮度不均、面积较大等特点，难以对其具体分布直接建模。传统灰度重心法提取光条中心线精度高、时间复杂度低，但受噪声光斑影响大，因而不能较好地处理上述问题。

针对实际工业场景中的上述问题，目前已研究的解决方法主要是对测量系统^[10-12]、图像预处理方法^{[9, 13-14]}和重心计算方法^[15-18]的改进，有学者对金属被测物表面反射光的偏振性质进行了研究^[10-12]，分别对传统多目、双目立体测量系统进行了改进，并在入射光路和接收光路中分别加入偏振片并使得两偏振片方向垂直，以消除测量时镜面反射光的影响，这类系统复杂、成本较高，且仅适用于激光入射角小于30°的情况。在图像预处理阶段引入新的处理方法，以尽可能剔除图像中的噪声光斑，这类方法不考虑环境光带来的误差、适用范围小，且不能完全去除光斑的影响^{[9, 13-14]}。有学者根据光条灰度分布特点引入权值，对传统重心计算公式进行改进，这类方法并未对噪声光斑进行处理，因此在含有光斑噪声、预处理效果较差的图像上提取精度低^[15-18]。

本文中提出一种新的中心线提取方法，该方法首先通过均值滤波、伽马校正和大津法进行图像预处理，得到分割后的图像，随即根据各像素点的灰度增量将光条横截线划分为多个不同的像素点子集，在不经阈值选取的情况下，同时对各子集分别提取灰度重心，即得到中心线预提取图像，在该图像中，激光与光斑两者的中心线同时存在，但激光中心线具有高连通性、大规模点集等特点，在中心线最终提取阶段，使用基于连通性的密度聚类算法对中心线预提取图像中各像素点进行聚类分析，最后激光中心线被准确提取，而光斑中心线被作为异常点进行剔除，该方法在剔除光斑的同时保持了图像细节，因此具有更高的提取精度。

灰度重心法^[9]根据激光光条横截线上各点的灰度值与位置信息来确定中心线的位置，具体来说，该方法根据预先选定的灰度阈值g_th对光条横截线上各点的灰度值g进行阈值选取：

式中，g′表示经阈值选取得到的灰度值，灰度重心的计算方法可以表示为：

式中，g_l, g_u表示经剪切后的光条横截线上的灰度范围，x_l, x_u分别表示g_l, g_u所对应的图像横坐标，作为一种亚像素精度提取方法，该方法计算简单、提取精度较高，且充分考虑到图像的灰度信息，即使光条灰度分布不均匀也能够达到较高的提取精度，但当阈值g_th选取不当且图像噪声较大时，灰度重心的计算会引入噪声误差，导致最终提取到的光条中心线与实际值具有较大偏差，其次在处理具有复杂形状光条的区域时，该法极易产生偏差，需要借助特定的图像预处理技术。

密度聚类属于非监督式机器学习算法，该法假设样本点分布的紧密程度决定聚类结构，从样本密度的角度考察样本点之间的连通性，并基于可连样本扩展聚类簇以获得最终聚类结果。具有噪声的基于密度的聚类方法(density-based spatial clustering of applications with noise，DBSCAN)^[19]作为密度聚类中的代表性算法，该算法对数据集中某样本点x的ε领域进行定义，其中，ε领域被定义为以x为中心、ε为半径的(超)球形区域，邻域中所含样本点数量决定x是否为核心对象，并根据样本点与核心对象之间的关系定义密度直达、密度可达和密度相连，数据集中所有样本点被划分为3类：(1)核心点：核心点即核心对象；(2)边界点：位于核心对象的ε领域上和领域中的样本点；(3)噪声点：非核心点、非边界点的样本点。簇的定义为:数据集中由密度可达关系导出的密度相连样本的最广泛集合，并满足以下两条属性：(1)连接性：簇中任意两点均密度可达；(2)最大性：所有密度可达的点必定位于同一个簇中。

DBSCAN具有Ο(m²)的时间复杂度，其中m是数据集的样本点数，使用类似k-D树的处理方式，其时间复杂度可以降至Ο(m×log₂ m)，DBSCAN仅需存储数据集中各样本点的类型(核心点、边界点或噪声点)，因此具有Ο(m)的空间复杂度。

分别在带噪声的圆形数据、带噪声的月牙形数据、各向异性分布数据、不同方差的气泡形数据、相同方差的气泡形数据上执行上述各种聚类算法，并使用“调整后德兰系数”(adjusted Rand index，ARI)作为性能度量标准，样本点数m=1500时，DBSCAN与k均值聚类(k-means)、凝聚层次聚类(aggregation level clustering)、谱聚类(spectral clustering)的ARI和运行时间如表 1所示。可以明显看出，除某些特定分布的数据集以外，DBSCAN聚类算法的聚类性能和时间复杂度，都远远优于其它算法。

传统灰度重心法根据预先设定好的灰度阈值，对激光光条横截线上各像素点进行“清洗”，即在计算灰度重心时，仅考虑灰度值高于阈值的像素点，该法存在如下弊端：(1)受物体表面反射率和环境光影响，激光光条横截线上各像素点灰度不会呈现规则的高斯分布，因此, 执行阈值选取极易导致提取到的中心线存在偏差; (2)阈值选取不能消除高灰度值噪声点的影响，因此在计算灰度重心时会带入噪声误差，从而导致提取精度降低。针对传统灰度重心法阈值选取的弊端，密度聚类重心法丢弃阈值选取过程，并根据光条横截线的灰度分布，将光斑噪声和目标光条的中心线同时从背景中分别提取，密度聚类重心法的中心线预提取整体处理流程如图 1所示。

Figure 1.  The overall processing process of the algorithm

激光光条与噪声光斑在原始图像中近乎处于同一个水平范围内，取该部分图像的水平横截线会发现，横截线上的灰度分布呈现出多个可以被划分的像素点集，各点集均隶属于目标光条或某个噪声光斑，且各点集的灰度值由中心向两边逐渐降低。根据上述特点，中心线预提取的第一步即依据光条横截线灰度分布图中的“波峰”与“波谷”，将灰度值不为零的像素点集划分为两个或多个连通区域，这些区域分别隶属于光斑噪声和目标光条，图像横截线上各像素点灰度值分布如图 2所示。其中，纵坐标表示各像素点灰度值，灰度值范围由0~255，两波峰间存在明显的波谷，因此横截线上的像素点集被划分为两个连通区域。在上述点集划分过程中，“波峰”和“波谷”的确定至关重要，一般来说，欧氏空间中2维连续函数的波峰和波谷即为函数极值点，在图像处理中，假设横截线上像素点灰度分布符合x轴上的连续分布G(x)，那么在2阶导数存在时可以通过下述条件判断波峰与波谷：

Figure 2.  Gray distribution of light bar cross-section

式中，x_i表示横截线上第i个像素点的图像横坐标，G(x_i)表示第i个像素点的灰度值，G′(x_i)表示第i个像素点在图像横轴上的1阶导数，G″(x_i)表示第i个像素点在图像横轴上的2阶导数。在光条横截线上各像素点灰度满足离散分布、均不可导，且呈梯形分布时，单个波峰可能含有多个像素点，因而不能仅依据极值点定义考察某点与近邻点间的关系对波峰、波谷进行判断，上述方法在处理这类问题时不具可行性。

为解决上述问题，密度聚类重心法从灰度值增量的角度出发，对各像素点灰度增量给出如下数学定义：

式中，ΔG(x_i)表示横截线上第i个像素点的灰度增量。由灰度增量可知，波峰上必存在一点，使得该点左近邻点的增量不小于零且右近邻点的增量小于零，而波谷上必定存在一点，使得该点右近邻点的增量大于零且左近邻点的增量不大于零，数学形式定义为：

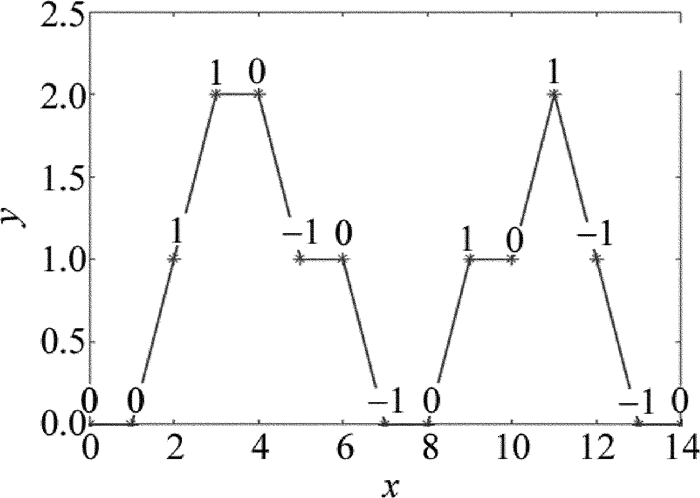
以图 3所示2维阶梯型离散分布为例，使用G(x)表征纵坐标y，得到ΔG(3)=1, ΔG(5)=-1，ΔG(10)=0, ΔG(12)=-1，ΔG(7)=-1, ΔG(9)=1，可以判定(4, G(4)), (11, G(11))为波峰，而(8, G(8))为波谷。在得到上述波峰、波谷后，即可对部分邻接的目标光条区域与噪声光斑区域进行边界划分，从而保证噪声光斑的高亮度像素点不会对目标光条产生影响，以便光条中心线预提取过程的进一步处理。

Figure 3.  Discrete functions

获取到每根光条横截线的划分边界点后，横截线上的整个像素点集被划分多个子集，各子集都分别隶属于目标光条或噪声光斑，考虑到传统灰度重心法使用阈值选取的弊端，在提取中心时忽略阈值选取过程，对各个子集直接计算灰度重心，从而保证目标光条的低亮度边缘不会由于阈值选取而丢失。中心线预提取阶段最终得到的图像中，目标光条和噪声光斑中心线均被完整保存，且目标光条不受噪声光斑影响。

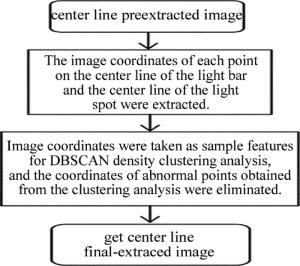
经中心线预提取阶段得到的图像中虽然存在一部分光斑中心线，但原始光斑区域得以大大缩减，光斑像素点数量与激光光条像素点数量间的比例下降，且激光中心线的细节得到了完整保持，至此光斑剔除问题转化为中心线选取问题。DBSCAN算法具有良好的时间复杂度和聚类精度，且算法本身不受簇形状影响，在激光中心线的最终提取阶段，将预提取得到的图像中各像素点的图像坐标作为聚类特征，并使用欧氏距离进行可连性分析，激光中心线具有更高的可连性，而噪声光斑中心线可连性低、像素点少，因而DBSCAN将激光中心线上各点聚类为一个簇，而噪声光斑中心线上各点被作为异常点剔除。通过密度聚重心法最终提取得到的图像中，噪声光斑中心线被完整剔除，且激光中心线的细节得到较好保持，密度聚类重心法的激光中心线最终提取流程如图 4所示。

Figure 4.  Final center line extraction process

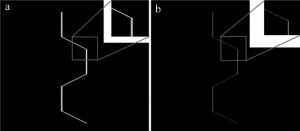
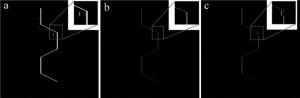
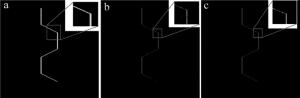
在图像预处理阶段，采用中值滤波对图像进行处理，为满足实时性的需要，且不丢失图像细节，采用小窗口(3×3)进行滤波处理，如图 5a所示。受环境光以及物体表面反射率影响，滤波后的图像仍存在对比度低、整体亮度高等问题，伽马校正在提高高亮度区域对比度的同时，可有效降低图像整体亮度，从而解决上述问题，采用该方法对图像进行增强处理，其中伽马系数置为γ=3，处理结果如图 5b所示。经伽马校正后的图像可明显区分目标与背景，但背景中仍存在灰度值较高的像素点，需要对图像进行阈值分割，考虑到各种分割算法的特点，分别采用迭代法、最大熵法^[20]和大津法^[21]对图像进行对比处理，处理结果如图 6所示。迭代法和大津法的分割精度较高，而最大熵法将一部分灰度值较高的背景区域误划分为目标，另外，迭代法需要手动设置阈值、时间复杂度高，因而最终采用大津法进行阈值分割处理。经大津法分割后的图像存在大量高亮度噪声，为方便后续提取中心线，需要采用小窗口(3×3)对图像进行闭运算形态学处理，图像预处理最终结果如图 7所示。

Figure 5.  Median filtering and gamma corrected image

Figure 6.  Image after threshold segmentation

Figure 7.  Image preprocessing results

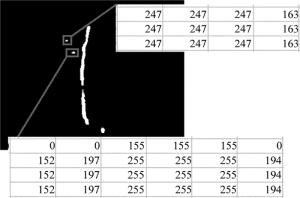
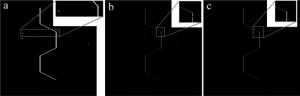
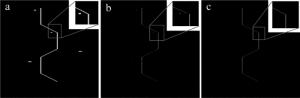
经预处理后的图像，图像细节和处理过程的实时性均得到保证，但受被测物表面反射率的影响而产生的大面积高亮度光斑噪声仍然存在，部分光斑噪声及其近邻像素点灰度分布如图 8所示。采用密度聚类重心法中的预提取过程对中心线进行提取，预提取图像如图 9所示。其中光条中心线并未受光斑噪声影响而出现部分缺失，但图中仍存在光斑噪声中心线，需要进一步提取，在密度聚类重心法的最终提取过程中，通过对预提取图像上各像素点的位置特征进行密度聚类，距光条中心线较远且包含像素点稀少的光斑噪声中心线被完整剔除，通过密度聚类重心法和传统灰度重心法分别提取到的光条中心线如图 10所示。可以明显看出，传统灰度重心法受光斑噪声影响，提取到的光条中心线严重偏离实际位置，而密度聚类重心法具有更高的提取精度。

Figure 8.  Gray-scale distribution of speckle noise in preprocessed image

Figure 9.  The results obtained by central line withholding

Figure 10.  Comparison of experimental results

向大小为600pixel×600pixel的图像中加入光条得到原始光条图像，图像中光条呈现左右不对称的高斯分布，光条及其真实中心线如图 11所示。分别向上述图像加入低亮度光斑、高亮度点噪声、高亮度小面积光斑、高亮度各向异性光斑进行仿真实验，观察实验结果如图 12~图 16所示。将提取精度定义为提取到的中心线与真实中心线之间各点的均方根误差(root mean square error，RMSE)e_RMSE，数学形式表示为：

Figure 11.  Original light bar image and real center line

Figure 12.  Centerline extraction without spot image

Figure 13.  Center line extraction of low-brightness isotropic spot image

Figure 14.  Centerline extraction of high-brightness point noise image

Figure 15.  Centerline extraction of high-brightness small-area spot image

Figure 16.  Centerline extraction of high-intensity anisotropic spot image

式中，x_i，y_i表示真实中心线上像素点的图像横、纵坐标，${{\hat x}_i},{{\hat y}_i}$表示提取到的中心线上像素点的图像横、纵坐标，Ω表示中心线上各像素点的图像横坐标集合，n表示中心线上像素点的数量，并对比运行时间，根据表 2可知，与传统灰度重心法相比，密度聚类重心法在高亮度各向异性光斑、高亮度小面积光斑、高亮度点噪声图像的均方根误差分别降低了12.59pixel, 15.12pixel和83.36pixel，时间复杂度分别提高了0.383s, 0.412s和0.416s, 该方法提取精度较高，对高亮度点噪声、高亮度小面积光斑以及高亮度各向异性光斑均具有良好鲁棒性，且两者时间复杂度近似。

预处理阶段使用小卷积核进行中值滤波，图像细节得到保持，采用伽马校正进行图像增强的方法在提高对比度的同时，降低图像整体亮度，缩小图像中高亮度光斑的区域，大津法进行自适应二值化不仅满足实时性的需求，还可以配合小卷积核闭运算处理，进一步缩小高亮度光斑。图 12~图 16中，传统灰度重心法受光斑噪声影响，噪声点附近的中心线出现明显缺失，而密度聚类重心法在同样的情况下仍然拥有较高的提取精度，由表 2中的实验数据可知，密度聚类重心法在应对高亮度点噪声、高亮度小面积光斑以及高亮度各向异性光斑等情况时具有明显优势，因此，在中心线提取阶段使用密度聚类重心法对含有高亮光斑的光条进行中心线提取时，可以提高提取精度。密度聚类重心法没有经过阈值选取过程，因此预提取阶段得到的图像中像素点较多，大多数聚类算法的时间复杂度随像素点数增多呈指数增加，但密度聚类重心法采用的DBSCAN聚类算法具有较低的时间复杂度，因此可以达到与传统方法近似的处理时间。

综上所述，这种密度聚类重心法可以在不改变光学测量系统的同时，较好地解决高反射率待测物的高光问题，相较于传统灰度重心法有较大提升，且时间复杂度近似。