Enhancement of attosecond pulse intensity based on inhomogeneous pump-probe laser field

阿秒脉冲的出现和发展使得人们能够探测原子、分子内电子的超快动力学现象。高次谐波作为现阶段获得单个阿秒脉冲的主要方法已经被广泛研究近30年^[1-3]。

强激光驱动原子、分子辐射高次谐波的过程可由1993年CORKUM提出的半经典“三步模型”^[4]来解释。CORKUM认为电子首先通过隧道电离进入连续态(电离过程)；随后，电子在激光场中加速并远离核子(加速过程)；最后，在激光场反向时部分电子返回核子并与核子发生碰撞进而辐射出高能光子(回碰及发射谐波过程)。随后，在1994年，由LEWENSTEIN等人^[5]提出了改进的量子理论，并考虑了量子干涉效应。基于上述理论，谐波辐射最大截止频率出现在I_p+ 3.17I/(4ω²)，其中, I_p为体系电离能，I和ω分别为激光强度和频率。由此可见，谐波辐射截止频率与激光光强和激光频率有关。因此，为了能够获得光子能量更高的脉冲，最简单的方案就是增强激光光强。但是，随着激光光强持续增大，电子在基态布局迅速减小，这导致谐波强度明显下降^[6]，显然不利于获得高强度的阿秒脉冲。除了增加激光光强之外，第2种延伸谐波截止频率的简单方案是利用波长较长的驱动激光场，例如，中红外激光场方案^[7]。但是，最近研究表明，随着激光波长的增大，谐波辐射强度呈下降趋势^[8]，这依然不利于高强度阿秒脉冲的产生。因此，为了克服上述方案中存在的问题，许多有效的改进方案被提出。例如：多色场组合方案^[9]、啁啾场频率调节方案^[10]、极化门方案^[11]等。

最近，随着激光科技以及纳米科技的发展，一种利用纳米结构表面等离子共振增强现象来增强激光强度，进而驱动原子、分子辐射高次谐波的技术得到了广泛关注^[12-14]。这里由于纳米结构的作用，激光场呈空间非均匀性。例如：KIM等人把惰性气体和激光场输入到金属纳米结构下，实验上获得了一个波长在47nm的脉冲^[12]。该方案的提出使研究人员可以利用较弱激光场来获得阿秒脉冲，这对阿秒科学的发展非常有利。随后，YAVUZ等人研究了金属纳米结构下原子空间位置对谐波辐射的影响^[13]。CAO等人利用双色场非均匀场方案获得了脉宽在10as以下的超短脉冲^[14]。但是，由于在纳米结构下入射光强不能太强(避免击穿纳米结构)，这导致谐波辐射强度很弱。因此，有许多研究人员对这一杰出工作持怀疑态度。例如：SIVIS等人认为KIM等人的研究工作中所观测到的应该是等离子体而不是高次谐波辐射光谱^[15]。因此，如何增强空间非均匀场下谐波辐射强度在这一领域得到了很大关注。例如：FENG利用H₂⁺离子为模型，研究表明，随着H₂⁺振动态增大，谐波辐射强度会得到提高^[16]。但是，如何获得高振动激发态依然是一个问题。

本文中提出了一种利用抽运探测激光驱动H₂⁺来增强谐波辐射强度的方案。结果表明，在抽运探测激光驱动下H₂⁺的谐波辐射强度得到明显增强。随后，采用不对称非均匀激光场驱动H₂⁺，谐波截止频率可以进一步延伸，并且可获得脉宽在32as的脉冲。若无说明，本文中的a.u.表示原子单位(atomic units), 否则表示任意单位。

激光驱动H₂⁺的含时薛定谔方程为^[17-19]:

式中，H(t)为体系哈密顿量；ψ(z, R, t)为电子波函数；V(z, R)为势能项；m_p，R，z分别为核质量、核间距离以及电子坐标；t表示时间。

E(z, t)为空间非均匀场，可以表示为：

其空间非均匀形式为：

式中，z₀表示H₂⁺在纳米结构中的空间位置；E₈₀₀ (E₁₆₀₀)，ω₈₀₀ (ω₁₆₀₀)，τ₈₀₀ (τ₁₆₀₀)分别表示抽运以及探测激光场的振幅、频率和脉宽；t_d为两束激光场的延迟时间。

高次谐波频谱图可表示为：

式中，$a\left( t \right) = - \left\langle {\psi \left( {z, R, t} \right)|\left[ {H\left( t \right), \left[ {H\left( t \right), z} \right]} \right]{\rm{ |}}\psi \left( {z, R, t} \right)} \right\rangle $为偶极加速度; ω为谐波频次。由于谐波辐射能E=hω(h为普朗克常量)，因此在本文中，通过分析谐波阶次ω/ω₁₆₀₀来讨论谐波辐射频率。

阿秒脉冲瞬时强度I_SAP(t)可由谐波光谱的傅里叶变换获得：

式中，q为叠加谐波次数。

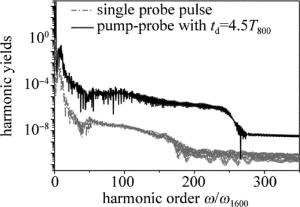
图 1给出H₂⁺在单色探测激光和抽运探测激光分别驱动下辐射的谐波光谱。抽运激光为15fs/800nm激光场；探测激光为10fs/1600nm激光场。2束激光场光强都为2.0×10¹⁴W/cm²。抽运探测激光延迟时间为t_d=4.5 T₈₀₀(T₈₀₀表示800nm激光场光学周期)。由图可知，在单色探测激光驱动下，谐波截止频率大致在160ω₁₆₀₀附近。随着抽运激光的引入，不仅谐波截止频率可以延伸到245ω₁₆₀₀附近，而且谐波辐射强度也有400倍的增强。这里需要指出是, 本文中对2束激光延迟时间对谐波光谱的影响同样做了研究(延迟时间从t_d=0到t_d=6.5T₈₀₀)，研究发现，当t_d=4.5T₈₀₀时, 谐波光谱有最好的增强效果。因此，图中只给出t_d=4.5T₈₀₀条件下的谐波光谱。

Figure 1.  Harmonic spectra from H₂⁺ driven by the single probe pulse and the pump-probe pulse

图 2中给出了上述2种激光场的波形、谐波辐射的时频分析图^[20]，以及核间距R随时间的演化图(虚线)。首先基于三步模型可知，谐波辐射每半个光学周期发生一次，因此对于本文中采用的激光场应该存在多个谐波辐射能量峰。但是，对于单色探测场情况如图 2a所示，只能观测到2束强度非常弱的谐波辐射能量峰(峰1：2.5T₁₆₀₀~3.0T₁₆₀₀；峰2：3.0T₁₆₀₀~3.5T₁₆₀₀)(T₁₆₀₀表示1600nm激光的光学周期)。分析核间距R随时间的演化图可知，在单色探测场驱动下，H₂⁺核间距离变化比较小(R < 3.0a.u.)，依然在夫兰克-康登(Franck-Condon，FC)区间，这导致电子电离几率非常小。这是谐波时频分析中只观测到2束强度非常弱的谐波辐射能量峰的原因。对于抽运探测场情况如图 2b所示，在抽运激光驱动下，H₂⁺核运动可以逃离FC区间，并且可以达到R=4.0a.u.附近，满足1sσ_g和2pσ_u态的3光子共振电离条件^[21]，这导致电离几率增大。随后在探测激光场驱动下，谐波辐射呈现3个高强度的谐波辐射能量峰，标记为P₁~P₃。这是谐波辐射强度增强的本质原因。

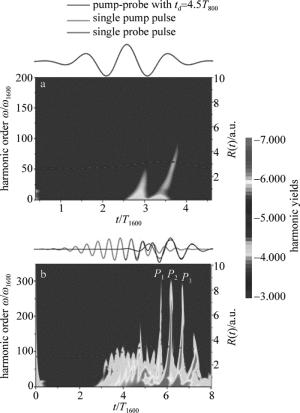
Figure 2.  Laser profile, the time-frequency analyses of the harmonic spectra and the time-dependent nuclear motion

由上述分析可知，当采用抽运探测激光驱动H₂⁺时，由于多光子共振电离的作用，谐波辐射强度可以明显增强。但是分析图 2b可知，谐波光谱的平台区仍然有3束谐波辐射能量峰共同作用产生，这显然不利于单个阿秒脉冲的产生。如何获得单一的谐波辐射能量峰是需要解决的另一个问题。由之前的研究可知^[22]，在空间非均匀场下，适当调整入射气体位置时，驱动激光场会呈现空间不对称性，这导致谐波辐射过程可以得到进一步调节。因此，图 3a中给出了H₂⁺入射位置在z₀=±100a.u.时抽运探测激光驱动H₂⁺的谐波辐射光谱。由图可知，当H₂⁺入射位置远离纳米结构中心时，谐波截止频率可以进一步延伸到340ω₁₆₀₀附近。但是H₂⁺沿正(z₀=100a.u.)、负(z₀=-100a.u.)方向入射时，谐波结构明显不同。具体来说，当z₀=100a.u.时，不仅谐波截止频率得到延伸；而且谐波辐射强度几乎保持不变。但是，当z₀=-100a.u.时，虽然谐波截止频率得到延伸，但是谐波辐射强度明显下降。图 3b~图 3d中给出了抽运探测激光时空演化图及z₀=±100a.u.时谐波辐射时频分析图。首先，在纳米结构下，由于等离子共振增强效应入射激光强度会明显增强并呈现空间非均匀性^[12-14]。但是，当H₂⁺空间位置远离纳米结构中心时，激光增强呈现不对称性。具体来说，(1)当z₀=100a.u.时，激光在z> 100a.u.时的增强效果要大于z < 100a.u.时的情况, 在这种情况下，当电子电离后，其沿z>100a.u.时(E(t)>0)的加速效果要明显高于z < 100a.u.时(E(t) < 0)的情况，这导致其在z>100a.u.(E(t)>0)加速下会获得更大的能量，因此导致谐波辐射能量峰的延伸，如图 3c中能量峰P₂(6.0T₁₆₀₀到6.5T₁₆₀₀)所示; (2)当z₀=-100a.u.时，激光在z < -100a.u.时的增强效果要大于z>-100a.u.时的情况, 在这种情况下，当电子电离后，其沿z < -100a.u.时(E(t) < 0)的加速效果要明显高于z>-100a.u.时(E(t)>0)的情况，这导致其在z < -100a.u.(E(t) < 0)加速下会获得更大的能量，因此导致谐波辐射能量峰的延伸，如图 3d中能量峰P₁(5.5T₁₆₀₀~6.0T₁₆₀₀)和P₃(6.5T₁₆₀₀~7.0T₁₆₀₀)所示。比较图 3c和图 3d可知，当谐波频率大于200ω₁₆₀₀时，对于z₀=100a.u.的情况，只有单一的辐射能量峰P₂对谐波光谱有贡献作用，这显然达到单个阿秒脉冲输出的要求。但是，对于z₀=-100a.u.的情况，谐波平台区的贡献来自于P₁和P₃的贡献和，这不利于单个阿秒脉冲的产生。

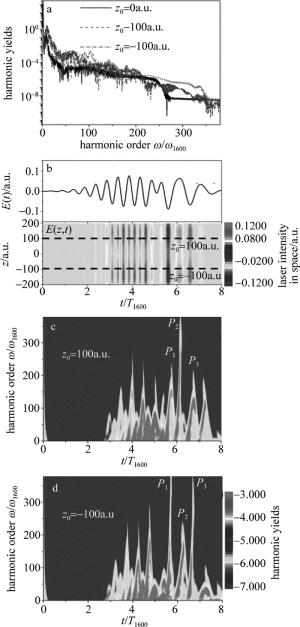
Figure 3.  a—harmonic spectra from H₂⁺ driven by the pump-probe pulse with z₀=±100a.u. b—the laser profile of the pump-probe in time and space c, d—the time-frequency analyses of the harmonics for the cases of z₀=±100a.u.

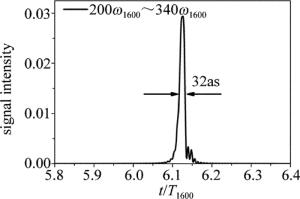
由上述分析可知，当H₂⁺沿正方向偏离纳米结构中心入射时(例如：z₀=100a.u.)，不仅谐波截止频率可进一步延伸；而且谐波频率大于200ω₁₆₀₀时，谐波平台区只由单一谐波辐射能量峰贡献产生，这满足单个阿秒脉冲输出的条件。因此，通过傅里叶变换谐波光谱并且叠加谐波光谱的200次(200ω₁₆₀₀)~340次(340ω₁₆₀₀)谐波，可获得一个脉宽在32as的单个阿秒脉冲，如图 4所示。由于采用了抽运探测技术，该谐波光谱强度(或者阿秒脉冲强度)比单色探测场情况下增强400倍。

Figure 4.  Temporal profile of the attosecond pulse

本文中提出了一种利用抽运探测激光驱动H₂⁺来增强谐波辐射强度的方案。结果表明，在抽运探测激光驱动下，由于多光子共振电离的作用，H₂⁺谐波辐射强度可以明显增强。随后，当H₂⁺沿正方向偏离纳米结构中心入射时(例如：z₀=100a.u.)，不仅谐波截止频率可进一步延伸, 而且谐波平台区只由单一谐波辐射能量峰贡献产生。最后，通过叠加傅里叶变换后的谐波平台区可获得脉宽在32as的脉冲。该脉冲强度比单色探测场情况下增强400倍。