Map
HTML
-
光子晶体光纤(photonic crystal fiber，PCF)也称微结构光纤，其包层上通常排列着形式奇特的气孔且气孔的折射率较为复杂，这些气孔的尺寸量级在微米级，贯穿整个器件，传导光波可以被严格地限制在低折射率的纤芯中[1-2]。光子晶体光纤的传输取决于空气孔尺寸和排列方式这两个方面，由于光子晶体光纤结构上存在灵活多变的可控性，使其比传统光纤拥有更多优越的传输特性，例如：无截止单模、非线性效应、奇异的色散、高双折射特性、可控的模场面积等[3-5]。
波分复用系统在当今得到了广泛的应用，系统要求的光纤总色散尽量减小到零且能够在较大波长的范围内实现良好的色散平坦。研究分析表明，在设计光纤时, 适当地优化其结构参量，能够获得在较大波长范围内的近零平坦色散，使其达到波分复用系统中的要求[6]。至今学者们已提出了很多新颖的光纤结构：2005年，WU等人提出了一种方形渐变气孔的微结构光纤[7]；2009年，ZHAO等人提出组合方形空气孔微结构光纤获得较低的色散平坦[8]；2011年，GONG等人提出多层环形气孔的密集结构获得高且平坦的色散[9]；2015年, KARASAWA提出在传统光子晶体光纤中心填充液晶，调控温度获得良好的色散特性[10]；2015年, KONG等人设计了一种圆形结构的双芯色散补偿型光子晶体光纤，主要利用掺杂的方式来实现[11]。如上所述，可以通过更改结构和掺杂来获得良好的色散特性。
在本文中，以提高光子晶体光纤的色散平坦特性为目的，研究结构参量及填充方式对其色散特性的影响。
-
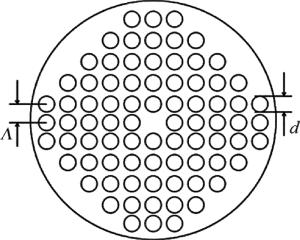
本文中设计的光子晶体光纤结构如图 1所示。它的原型是空气孔以11×11矩阵排列的四方晶格，如图所示的八边形结构是在其基础上微调获得的。模型中的空气孔直径是d，孔间距为Λ，空气填充率则用d/Λ表示。设置包层材料的折射率nm=1.45，气孔的折射率n=1。
Figure 1. Cross section of PCF
PCF的总色散系数为材料色散系数和波导色散系数这两者的总和[12]。由于光纤的基底材料折射率对波长的依赖性，由此产生的材料色散可表示为：
式中, c为真空中的光速，λ为光纤中传输光的波长，nm为材料折射率，可通过Sellmeier方程计算。与光纤的包层结构参量密切相关的色散称作波导色散系数Dw(λ)，其计算公式如下：
式中, neff为模式的有效折射率。由此可得到的光纤总色散系数可表示为：
目前，很多分析光纤导波模式的理论方法得到发展和普及，如：有效折射率法(effective index method，EIM)[13]、时域有限差分法(finite difference time-domain，FDTD)[14]、平面波展开法(plane-wave expansion method，PWEM)[15]、有限元法(finite element method，FEM)[16]等。其中，有限元法的应用较为广泛，其在分析光波导的模场方面有较高的计算精度，对于任意形状不规则、任意排布的空气孔、任意材料折射率组合的情况下也相当适用。利用该方法对光纤的色散特性能够进行分析、建模和计算都较为方便。有限元法的基本原理是：根据Maxwell方程，可以推导出光子晶体光纤遵循的本征值方程：
式中，磁场强度是H，介电常数和磁导率分别为εr和μr, 光波角频率为ω。其计算基本过程是：(1)构建模型；(2)设定波长、材料折射率、子区域及边界条件；(3)计算区域离散网格化，在每个小区域求解(4)式，然后综合所有小区域内的解，得到整个计算区域上的解；(4)进行解后处理[17-18]。
本文中采用有限元法对所提出的PCF结构进行模拟分析。根据仿真结果讨论了结构参量、不同材料、两种填充方式对PCF色散系数的影响。
-
结构参量很大程度上决定了光子晶体光纤的性质，下面讨论空气孔直径d和孔间距Λ对色散的影响。
-
首先考虑保持孔间距Λ不变的情况下，空气孔直径变化对色散特性的影响。本研究中Λ取为2μm，空气孔直径d取5个值，分别为0.8μm, 1.0μm, 1.2μm, 1.4μm, 1.6μm，即空气填充率d/Λ从0.4变化到0.8。通过计算获得基本模场，有效折射率和色散系数，如图 2所示。
Figure 2. Relationship between some parameters and wavelength under different d when Λ=2μm
图 2a是基本模场图和有效折射率随波长的变化曲线，很容易观察到：光纤随着空气孔直径的增大，在同一波长处的有效折射率减小，当波长增加时，有效折射率也减小。再利用(1)式、(2)式和(3)式，获得波长和色散系数的关系，如图 2b所示:空气孔直径减小时，零色散点沿着长波的方向移动；在长波区域，零色散波长随着空气孔直径的增大也沿长波方向移动。所以若是将零色散波长增大到长波区域，只需要保持Λ不变，减小空气孔直径d，也就是减小空气填充率d/Λ就可以实现。由计算可知，在1550nm附近处，随着空气孔直径的增加，5条曲线对应的色散系数如表 1所示。数据表明：当孔间距Λ不变时，从直径从0.8μm增加到1.0μm时，在1550nm处的色散系数增长率为122%，而在d从1.4μm增加到1.6μm时，色散系数的增长率只有13.4%，这种结果表明，在波长1550nm处，空气孔直径d=1.6μm时，曲线较为平坦。
d/μm 0.8 1.0 1.2 1.4 1.6 D/(ps·nm-1·km-1) 26.30 55.82 77.54 95.40 108.20 Table 1. Dispersion coefficient corresponding to different air hole diameter at 1550nm wavelength
-
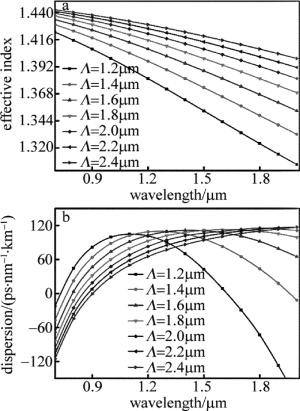
令空气填充率d/Λ=0.8，然后通过改变孔间距Λ来获得其对色散系数的影响，取Λ分别为1.2μm, 1.4μm, 1.6μm, 1.8μm, 2.0μm, 2.2μm以及2.4μm。获得的有效折射率随波长的变化关系以及色散曲线如图 3所示。
Figure 3. Relationship between some parameters and wavelength under different Λ when d/Λ=0.8
从图 3a中看出，在相同的波长处，有效折射率会随着孔间距Λ的增加而增大，而在相同孔间距Λ的情况下，有效折射率随着波长的变化而减小。在图 3b中，随着孔间距Λ的增加，零色散波长向着长波方向移动。波长增大时，色散系数先增加后减小。在1550nm处，随着Λ的增加，获得的色散系数如表 2所示。Λ由1.2μm增加到2.4μm时，计算得到色散系数增长率分别为245.8%, 21.4%, 2.7%, -3.7%, -4.2%, -5.8%，随着Λ增大，色散系数先增大后减小，而且色散系数在Λ较小的时候，变化特别明显，从图上可以观察到，Λ=2μm时，色散曲线比其它曲线要更为平坦，在1550nm处，色散系数值为108.20ps/(nm·km)。
Λ/μm 1.2 1.4 1.6 1.8 2.0 2.2 2.4 D/(ps·nm-1·
km-1)26.03 90.03 109.32 112.33 108.20 103.62 97.60 Table 2. Dispersion coefficient with different air hole spacing at 1550nm wavelength
-
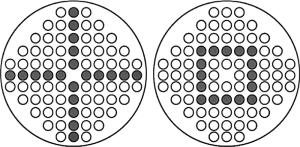
前面通过选择合适的结构参量，在通信波长1550nm处，获得色散平坦曲线。通过文献可知：通过优化结构参量都可以得到良好的平坦性，但色散系数的值仍然偏大，如WU等人获得的色散系数值大约为80ps/(nm·km); GONG等人获得的色散系数值为350ps/(nm·km); ZHAO获得的结果大约为60ps/(nm·km)以及仿真中所获得的108.20ps/(nm·km)。这些数据说明仅仅通过调整结构参量来降低色散还是有限的，因此为了降低色散系数值，可以在包层空气孔中填充材料来实现[19-21]。填充材料选用的是液态CO2、普通酒精和质量分数为0.8的糖溶液，它们的折射率分别为1.2，1.36以及1.49。本文中主要讨论“十”字形和“口”字形两种填充方式，这两种方式如图 4所示。
Figure 4. Two filling methods: "十" shape and "口" shape
-
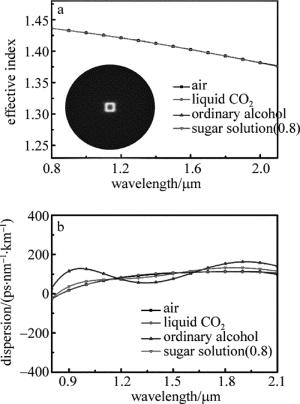
利用有限元法计算出由“十”字形填充方式获得的有效折射率随波长的变化关系以及色散曲线，计算结果如图 5所示。
图 5a是光子晶体光纤的场分布和有效折射率随波长的变化关系，随着波长的增加，有效折射率减小，当以“十”字形填充不同材料时，光子晶体光纤整体的有效折射率随着材料折射率增大而变大，而当填充物是质量分数为0.8的糖溶液，即材料折射率为1.49时，光子晶体光纤的有效折射率整体上移。图 5b是当波长取值在0.8μm~2.1μm范围内，可以获得色散平坦较好的曲线，根据曲线所示，当填充液体CO2和普通酒精时，色散平坦特性依旧优良，且填充普通酒精时，其色散值更小，拟合出来的结果为20.39ps/(nm·km)，色散变化明显，较之调整结构获得的结果要优化得多，色散系数减小到接近普通单模光纤G.652在波长1550nm处的色散值，更加符合光纤色散在应用窗口内的要求。
Figure 5. Relationship between some parameters and wavelength with "十" shape filling method
-
计算步骤和前面一样，通过仿真计算出有效折射率随波长的变化关系和色散曲线，仿真结果如图 6所示。
Figure 6. Relationship between some parameters and wavelength with "口" shape filling method
图 6a是以“口”字形填充不同材料后获得的基本模场图和有效折射率与波长的关系图。从图中获得的有效折射率随波长变化关系就不再那么明显，4条曲线几乎重叠，有效折射率随波长的增加而减小。在图 6b中，波长范围为0.8μm~2.1μm，填充液体CO2和填充空气的结果差不多，两条曲线几乎重合，当填充其他两种材料时，色散系数曲线变得不太稳定，开始波动，且填充普通酒精时，波动最为明显。因此，“口”字形填充所获得的结果不能得到减小色散的理想效果，反而使得色散平坦性变差，远远不如“十”字形填充后的结果。
2.1. 结构参量对色散系数的影响
2.1.1. 气孔直径d对色散系数的影响
2.1.2. 气孔间距Λ对色散系数的影响
2.2. 填充方式对色散系数的影响
2.2.1. “十”字形填充对色散系数的影响
2.2.2. “口”字形填充对色散系数的影响
-
为了获得较好的色散平坦光子晶体光纤，微调四方晶格获得一种非正八边形的结构，基于有限元法，利用结构参量、两种不同的填充方式以及3种不同的填充材料，仿真计算获得色散特性曲线。先通过改变空气孔直径d和孔间距Λ得到色散曲线最为平坦的结构参量，即研究的波长范围在0.8μm~2.1μm之间，Λ=2μm，d=1.6μm时，获得的色散曲线最为平坦，此时在通信波长1550nm处的色散系数值为108.20ps/(nm·km)。由于色散系数值偏大，所以通过填充液体材料来减小色散值，文中采用“十”字形和“口”字形两种填充方式，仿真结果发现：“口”字形填充的色散平坦效果达不到预期，而“十”字形填充液体材料时，当波长取值在0.8μ~2.1μm范围内，填充液态CO2和普通酒精都能获得比填充空气时更好的色散平坦特性，特别是在填充普通酒精时，不仅色散曲线保持着良好的平坦性，而且在波长1550nm处的色散系数更低，其值为20.39ps/(nm·km)，和G.652单模光纤在1550nm处的色散系数值接近，符合光纤色散在应用窗口内的要求。本文中的结果对实际设计该种类型的光子晶体光纤具有指导作用。
DownLoad: