Broadband THz absorbers based on graphene and 1-D photonic crystal

人们对光子晶体的研究通常是考虑它对光波的反射和透射，很少研究它对光波的吸收。光波吸收器件是指把入射的光波电磁能量转化为热能或其它形式能量的一种结构，它在太阳能收集^[1-2]、热电转换^[3]、传感^[4]、红外探测^[5]、热辐射调制^[6-7]等领域有着广泛的应用。考虑到容易加工，基于金属和介质组成的一维层状结构是常见的电磁波吸收器的构型^[8-10]。但普遍存在吸收效率低、对入射方向敏感等问题。近年来石墨烯由于具有非常独特的电学和光学性质^[11-12], 被广泛应用于各种光电子器件的研究当中。但由于石墨烯的厚度极薄, 小于1nm, 从而其光吸收率很低, 限制了石墨烯在光吸收领域的应用。为了增强石墨烯的吸收效应，人们开始借助光子晶体结构和超材料结构^[13-16]。最近LIU等人研究发现, 当石墨烯位于光子晶体表面时, 石墨烯和间隔层在光子晶体表面构成了表面缺陷, 从而导致光的局域化。这种局域化将使得由石墨烯能带间跃迁所导致的可见光光吸收被增强大约4倍^[13-14]。XIANG和NEFEDOV等人利用基于石墨烯的双曲型超材料结构实现了电磁波的完美吸收^[15-16]。NING等人基于石墨烯光子晶体实现对特定波长光的吸收^[17]。但上述研究还是面临着吸收率较低或者带宽较窄的问题。从实际应用角度看，宽带高吸收的器件更为重要。本文中利用1维光子晶体独特的传输机制并结合石墨烯材料，实现宽带高效率的吸收。

石墨烯的性质主要由其电导率来决定，在高频情况下可采用Kubo模型来描述^{[15-16, 18]}，其表面电导率表示为σ_G(下标G表示石墨烯):

式中, ω是入射光角频率，e是电子的电量，$\hbar $是简约普朗克常数，k_B是玻尔兹曼常数，T是温度，E_F是费米能，τ是电子弛豫时间，i是虚数单位。石墨烯是单层原子结构，其厚度小于1nm。对单层石墨烯结构，电磁波入射到石墨烯表面经历的反射和透射行为与普通介质层明显不同，所以必须采取特殊的分析方法。参考文献[19]中从麦克斯韦方程组所要求的电磁场边界条件出发，借助传输矩阵方法推导出电磁波在石墨烯表面的传输规律。本文中利用同样的原理研究石墨烯与1维光子晶体的复合结构对光波的吸收规律。

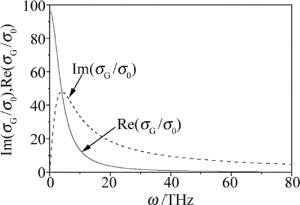
石墨烯对电磁波特殊的作用表现在其电导率上。在电场作用下, 石墨烯产生表面电流，从而把电磁能量转化为其它形式的能量。为此在E_F=0.45eV，T=300K, τ=0.25ps时, 画出石墨烯电导率的实部和虚部随频率的变化，如图 1所示。可以发现, 电导率的实部在0THz~20THz范围有较大的值，20THz以后迅速衰减。电导率的实部换算成介电常数时对应介电常数虚部，衡量吸收的大小。图 1中的结果为后面的研究提供了分析的基础。

Figure 1.  The real and imaginary parts of graphene conductivity

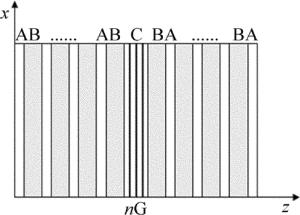
设计模型如图 2所示。1维光子晶体由两种介质层A、B交替沿z轴分布而成，中间一层材料与A层相同，但厚度不同，在其中等距离嵌入n层石墨烯G，该层表示为C。介质层A和B的折射率和厚度分别为n_A=2.5, d_A=0.15mm, n_B=1.5, d_B=0.25mm。两介质层光学厚度相等，整个结构放置在空气背景介质中。上述结构参量的选取是为了使考虑的频谱落在0THz~ 20THz范围以内，在这个范围石墨烯的吸收最为明显。入射面为xz平面。对H极化电磁波，磁场只有y分量，在任一介质层内，电磁波是正反两个方向平面电磁波的叠加，表示为:

Figure 2.  Compound structure of grapheme and 1-D photonic crystal

式中，k_x表示波矢的切向分量，在传输过程中保持不变; k_z是波矢的z分量。由麦克斯韦方程可以推导对应的电场为x分量，表示为:

式中，ε₀和ε_r分别是真空介电常数和介质的相对介电常数。当电磁波在两种普通介质层(分别用下标j和i表示)的界面过渡时，电场和磁场在切向(x, y方向)的分量均保持连续，用矩阵表示:

式中, 是j(或i)层介质的折射率。于是有，其中$ {\mathit{\boldsymbol{T}}_{ji}} = {\mathit{\boldsymbol{T}}_j}^{ - 1}{\mathit{\boldsymbol{T}}_i}$称过渡矩阵。

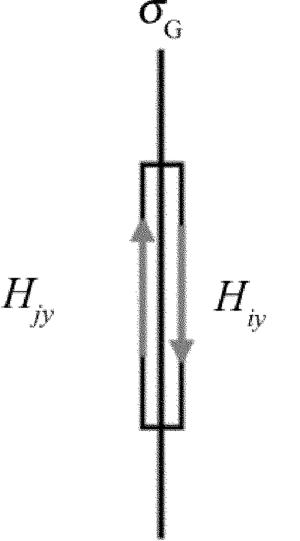
在图 2所示的结构中，由于石墨烯的厚度小于1nm, 故可以把它看作是没有厚度的界面。当电磁波从j层经过石墨烯过渡到i层时，由于石墨烯存在表面电流，导致磁场的切向不再连续，如图 3所示。

Figure 3.  Electromagnetic boundary of grapheme surface

边界过渡条件变为:

(5) 式左边是磁场沿图 3中矩形闭合回路的环量积分。结合(3)式有:

于是(4)式变形为:

此时过渡矩阵$ {\mathit{\boldsymbol{T}}_{ji}} = {\mathit{\boldsymbol{T}}_j}^{ - 1}{\mathit{\boldsymbol{T}}_i}$与不存在石墨烯的情况完全不同。在图 2结构处于空气背景中(j=0)，电磁波前后界面处的入射场H_in、反射场H_r和透射场H_t的关系可以通过以下矩阵计算:

式中, 表示j层内正反两个方向平面电磁波相位的变化, d_j是j介质层厚度，N为结构周期。由此得到结构透射率t、反射率r和吸收率A计算公式:

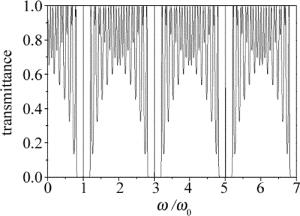
基于图 2的结构(AB)⁶C(BA)⁶，选取基频${\omega _0} = \frac{{{\rm{ \mathsf{ π} }}c}}{{{n_{\rm{A}}}{d_{\rm{A}}} + {n_{\rm{B}}}{d_{\rm{B}}}}} = 1.257{\rm{THz}} $，相对基频波，每层介质均为λ/4波片，中间层厚度d_C=2d_A，c是光速。首先C层，不嵌入任何石墨烯层，在不同ω的条件下计算透射率，得到图 4所示的光子晶体的带隙结构。禁带中心均位于基频的奇数倍处，禁带中心有一个完美的透射峰对应缺陷模式。在后面的计算中，入射方向均为z轴正向。注意到通带的透射谱并不是平坦的直线，而是由一系列振荡的子峰构成。1维光子晶体的传输机制是周期结构的布拉格散射和微腔耦合共振共同形成。图 2中每一个介质层相当于一个共振微腔，微腔共振模式由于耦合形成分裂，分裂模式的个数等于微腔的个数。通带中每一个子峰实际上都是对应微腔的分裂模式。注意到透射谱通带共有24个子峰，恰好对应一个周期介质层的个数。这是最常见的1维光子晶体的带隙结构，本文中就是利用这种1维光子晶体共振透射的属性结合石墨烯材料来实现宽带高吸收的光子器件。这里给出这个图形是为了给后面的研究提供对照和分析的基础。

Figure 4.  Band gap structure of 1-D photonic crystal

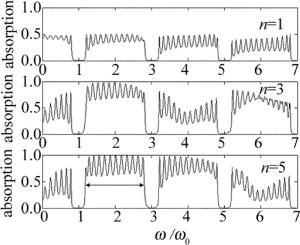
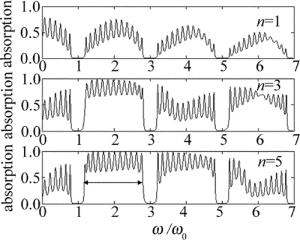
图 5显示了在C层插入不同层数石墨烯后结构的吸收谱。注意到无论n为何值，吸收谱的位置和宽度与图 4通带完全相同，原来的通带变成吸收带，这说明吸收完全依赖结构的透射，透射时光波与石墨烯发生作用，石墨烯的电导产生表面电流消耗电磁能量，导致光波的吸收。在带隙位置，由于电磁波被结构反射，电磁波无法与石墨烯发生作用，因此吸收为0。n=1时，所有吸收带的峰值小于0.5，随着n的增加，吸收带的峰值发生明显的变化，但每个吸收带的变化趋势不同。可以看到，n=5时，第2个吸收带(ω₀~3ω₀)除边缘2个子峰其余峰值全部达到1，而子峰的底部也全部大于0.6。这种宽带高吸收(如图中箭头所示)的结果在以往的基于石墨烯吸收的研究中很少见到，但其余吸收带的峰值不仅比第2个吸收带小，而且大小不一致。仔细观察发现, 每个通带位置的吸收峰的个数变为12，这同样可以得到解释。由于石墨烯位于两个周期结构的中间，前后周期结构的微腔共振无法产生耦合效应。前面的周期结构共有12个介质层，产生12个共振子峰，故形成12个吸收峰。实际上石墨烯的吸收主要取决于前面的周期结构的共振透射。为了验证这一点，去掉C后面的周期结构(BA)⁶，对结构(AB)⁶C进行类似图 5的吸收谱的计算，结果显示在图 6中。与图 5相比，除n=1时吸收带子峰的峰值不同外，n=3和n=5时吸收带的宽度和峰值分布完全相同。看到吸收谱均处于太赫兹频谱范围，THz频率电磁波由于具有特殊的性质, 在无损检测、医疗成像、雷达探测、通信等领域具有很广泛的应用，这里的吸收频谱同样具有特别的应用价值。

Figure 5.  Absorption spectra of (AB)⁶C(BA)⁶ while C layer was embedded with grapheme of n layers

Figure 6.  Absorption spectra of (AB)⁶C while C layer was embedded with grapheme of n layers

在图 6中，为达到宽带高吸收，选取n=5和第2个吸收带无疑是最优的，如图中箭头所示。造成吸收带之间差异的原因是，在C层中由于石墨烯造成界面的不连续，在石墨烯表面形成反射，因此在石墨烯之间也形成共振微腔，C层中微腔与前面1维光子晶体共振耦合造成光波多次往返穿越石墨烯，从而使吸收增强。但这种微腔共振与波长密切相关，第2个吸收带正好满足这个条件，所以吸收最大。其它吸收带由于共振条件不匹配，导致吸收峰值减小。由于微腔共振波长与微腔厚度成正比，所以如果增加嵌入C层的石墨烯层数n，微腔厚度变小，完美吸收峰将向高频吸收带移动。为此在图 6中结构(AB)⁶C的基础上，计算n=13和n=21时的吸收谱，结果如图 7所示。发现n=13时第3个吸收带(3ω₀~5ω₀)的子峰除第1个外其余峰值全部达到1，而n=21时，第4个吸收带(5ω₀~7ω₀)的子峰峰值全部达到1，如图中箭头所示。仔细观察发现，此时第3个和第4个吸收带子峰的个数均由原来的12变为11，这是由于n的增加导致吸收带子峰的带宽增加，但由于总的带宽保持不变，从而吸收谱边界子峰落入带隙位置，导致吸收子峰个数的减少。图 7中的结果说明，通过改变嵌入C层石墨烯的层数，可以改变完美吸收带的位置。

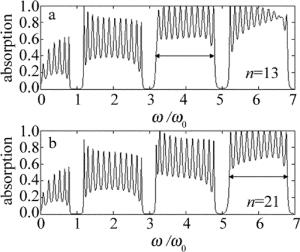
Figure 7.  Absorption spectra of (AB)⁶C while C layer was embedded with grapheme of 13 layers or 12 layers

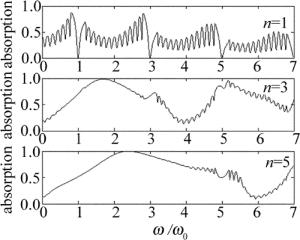
特别有意思的是，上述复合结构对光的吸收属性与入射方向有关。保持结构(AB)⁶C不变，改变入射方向从C方向入射，这时复合结构表示为C(BA)⁶，同样在C层插入不同层数石墨烯来计算结构的吸收谱。如图 8所示，发现图 8与结构相同但入射方向相反的图 6完全不同。除n=1有类似吸收带的分布外，n=3和n=5的吸收谱与1维光子晶体的通带完全没有了对应关系。这是因为光波在进入1维光子晶体之前已经和石墨烯发生充分作用，在n较大时，后面的周期结构对吸收谱没有了影响。

Figure 8.  Absorption spectra of C(AB)⁶ while C layer was embedded with grapheme of n layers

用数值方法研究了石墨烯和1维光子晶体的复合结构对光波的吸收属性，发现复合结构吸收谱具有类似1维光子晶体通带结构的吸收带结构。特定的吸收带由多个峰值为1的子峰构成，具有带宽大吸收率高的特征。该吸收带的位置可以通过石墨烯的层数进行调节。研究还发现，复合结构对光波的吸收结果与入射方向有关。该研究结果为相关光吸收器件的设计提供参考。