HTML
-
为了提高风廓线数据测量的准确度,降低低空风切变对飞行器起降落的威胁程度[1-3],近年来对测风雷达探测的径向风矢量反演3-D风场的信息中一般使用速度方位显示法、扩展速度方位显示法、体积速度处理法、速度方位处理法、匀速风场法、涡度-散度法等[4-6]。这些反演方法中基本附加了线性、局部均匀等强加假设条件,反演质量受限。国内外学者对提高雷达资料的质量做了大量工作。ZHANG[7]等人研究了风场干扰中生物的回波辨别踢除方法。ZHU等人[8]对风廓线数据做了平滑信号处理传送数据、对称性踢除杂波峰,前后一致性平均等预处理。在风廓线数据质量控制上对干扰信号如杂波干扰、噪声干扰都做了预处理。YU[9]介绍了使用拟合均方根误差及对称性的数据控制方法。在实际的雷达探测过程中风场收到扰动,风廓线观测常常有较大误差,风场准确性更加受限。
作者提出对时间域上风廓线数据使用后向传播灰色算法(back propogation grey method, BP-GM)进行控制。灰色算法最大的特点是可利用贫数据建模,而神经网络对非线性系统具有良好的控制效果。将BP-GM用于激光测风雷达原理样机中,试验结果表明, 该算法能有效地降低残差值,提高风廓线数据控制的精度。
-
1982年提出的灰色理论是通过累加原始数据系列,形成单调上升的线性或指数型的序列,通过拟合值找出规律,克服数据的随机性[10]。
获取数据样本X(0)={X(0)(1), X(0)(2), …, X(0)(n)},原始数据满足条件X(0)(i)≥0, (i=1, 2, …, n)。使用此数据样本建立GM(1, 1)模型[11]。根据数据样本累加生成序列X(1)={X(1)(1), X(1)(2), …, X(1)(n)},其中,$ {X^{(1)}}\left( i \right) = \sum\limits_1^i {{X^{(0)}}} (i)$。此累加序列的白化方程为$ \frac{{{\rm{d}}{\mathit{\boldsymbol{X}}^{(1)}}}}{{dn}} + a{\mathit{\boldsymbol{X}}^{(1)}} = b $,a为发展灰数,b为内生控制灰数[12]。
根据白化微分方程写成矩阵:
式中,a′为a的演化值。
根据最小二乘法,估计原始数据的拟合值:
式中,e为误差。建立模型之后对其精度进行检验。
残差是原始数值与拟合数值的差:
后验差比值C是残差方差Se2和数据方差SX2之比:
式中,e为误差的期望值, X为输入序列的期望值[13]。可以明显看出,残差方差越小,控制精度越高。数值大小与原始样本的数值有关,为了标准化,故而使用后验差比值。
灰色模型需要的控制数据量较少,样本分布可以是随机性的、计算简便,结果较准确。灰色算法是使用拟合的思想解白化方程来进行数据控制,其计算值具有单调性,对于具有波动性和随机性的风场数据而言,不能简单地满足单一的函数条件,因此控制数据结果并不理想。
-
BP神经网路是一种监督式的学习方法[14],根据输入的样本使用反向传播的思想对网络的权值、阈值和误差不断进行训练,使输出向量在误差允许范围内尽可能的接近期望向量,并保存网络权值和阈值。
神经网络训练过程如下。
(1) 初始化神经网络。输入集合X=(X1, X2, …, Xn),输出集合Y=(Y1, Y2, …, Ym), 隐层节点数为k, 输入层节点数为n, 输出层节点数为m, 初始化神经元之间的连接权值[15],输入层与隐层和隐层与输出层的连接权值分别为vih和who, 初始化隐层阈值和输出层阈值分别为ah和bo,初始化学习速率和神经元激励函数。
(2) 隐层输出。根据输入集合X和输入隐层的权值vih以及隐层阈值ah, 得出隐层的输出计算公式:
式中,f为隐层激励函数[16];h=1, 2, …, k;i=1, 2, …, n。
(3) 输出层输出。根据Ph和隐层与输出层的权值who以及输出层的阈值bo, 得出输出层的输出计算公式:
式中,o=1, 2, …, m;h=1, 2, …, k。
(4) 计算误差。根据预测输出量Qo和期望输出量Yo得出误差计算公式:
(5) 权值更新。根据网络预测的误差向量eo更新输入层与隐层、隐层与输出层之间权值vih和who:
式中,θ为学习速率。
(6) 阈值更新。根据误差向量eo更新输入层与隐层、隐层与输出层之间的阈值:
根据网络允许的最大误差判断算法迭代是否结束,否则继续更新隐层输出和阈值。
BP神经网络是常用的非线性拟合工具,具有广泛的适应能力、学习能力和映射能力。通过对历史的风场数据学习,网络能从无规律性的数据中获取各自的依存关系。BP神经网络也存在局部极小和收敛慢的问题,其运算参量和结构参量要根据经验来选择,缺乏理论上的指导。
-
优化数据控制算法的本质是求解残差函数的最小值问题[17]。灰色算法对贫数据具有良好计算控制能力,但是灰色算法对平滑度不够的数据集的残差通常会不能满足需求[18]。BP神经网络算法对非线性的数据有着强大的学习能力,理论上3层BP神经网络就能拟合任意的函数,但神经网络需要大量的数据进行训练才能保持原数据的特性,而且数据量不够时神经网络的误差也会很大[19]。为了使用这两种算法的优势,弥补各自的不足,现使用BP神经网络对灰色算法残差的多次修正[20-23],最终更新灰色算法的拟合值。
灰色理论与BP神经网络融合的风廓线控制算法过程如下。
(1) 获取数据样本,使用灰色算法预处理数据,计算残差集e(0)(i)。原始时间数据集X(0)(i),原数据的预拟合值X(0)′(i),则残差集为:
(2) 使用BP神经网络训练残差集。以残差集e(0)(i)作为BP神经网络的输入值训练网络,理想的残差为0,之后使用训练后的各权值和阈值对残差进行数据调整,得到调整后的残差集e(0)′(i)。
(3) 通过e(0)′(i)修正灰色算法中的值,得到XBP-GM(0)(i),其计算公式为:
(4) 为了尽可能地降低残差,使用修正后的值, 获取残差集eBP-GM(0)(i):
通过神经网络训练eBP-GM(0)(i),理想的eBP-GM(0)(i)对应的输出量是元素为0的集合。使用训练好的网络残差eBP-GM(0)′(i),最后更新出灰色算法的值:
灰色算法的残差是无规律性的,使用BP神经网络强大的学习、适应能力能有效地获取残差值的依存关系。两次使用BP修正,使得灰色算法的残差值能得到有效的控制,但是BP训练花费的时间比较长,两次使用BP也会增加残差的训练时间,整个灰色预测时间变得更长。
1.1. 灰色理论GM(1, 1)原理
1.2. BP神经网络原理
1.3. 基于BP神经网路的灰色风廓线质量控制算法
-
试验中采用研制的激光测风雷达原理样机,雷达系统自动化操作管理中心频率为160MHz,预留信号处理带宽60MHz,发射脉冲激光重频10kHz,脉宽200ns,单脉冲能量约60μJ,以采样率400MHz/14bit的高速采集卡对回波信号进行采集,使用1024点进行快速傅里叶变换,同时使用开发的回波信号处理算法对采集信号进行谱积累处理。雷达测风实验于2015-03-11下午在成都某楼顶进行,气温8℃,相对湿度60%,水平能见度约5km,垂直能见度约3km,实验场景如图 1所示。
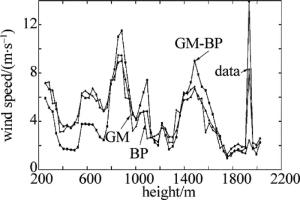
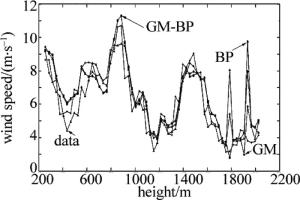
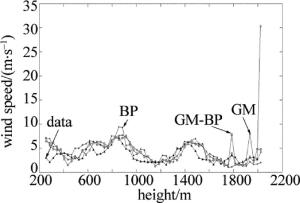
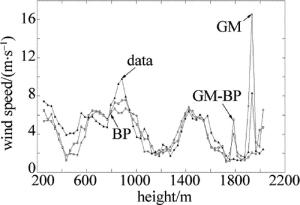
采用实时监测的风廓线数据进行分析。分别采用GM(1, 1), BP神经网络和BP神经网络修正GM残差模型实验,计算了的风廓线控制数据的相对误差、精度及后验差及小概率误差。在高度75m~2025m的67道数据以及时间段15:02:28~15:03:37的25道数据形成的67×25的数据矩阵计算GM模型、BP模型和GM-BP模型的相关属性。在此时间段使用原水平风速计算的GM, BP和BP-GM平均相对误差。通过GM和BP-GM计算获取的风廓线数据控制的效果图。
图 2~图 5中分别给出了特定时刻的风速控制效果。从图中可以看出,3种算法的控制值基本上符合原始数据值。为了详细说明这3种算法的效果,分别计算了残差值、后验差值以及精度值。
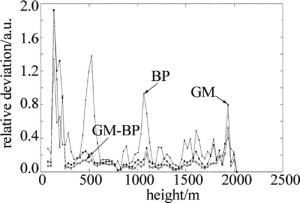
图 6中,3条曲线分别是水平风速在15:02:28~15:03:37时间段的3种控制算法平均相对误差值在高度上的变化情况。相对误差值越小,质量控制的效果越好。在75m~200m处存在奇异点,误差值波动大。从图中可以看到GM-BP控制的误差最小,几乎接近于0。
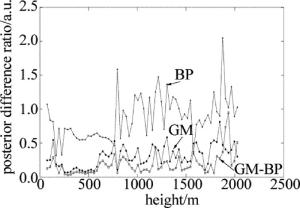
图 7中,3条曲线分别是水平风速在15:02:28~15:03:37时间段的3种控制算法的后验差比值在高度上的变化情况。后验差比值反应数据控制的有效情况,比值越小,控制效果越好。GM-BP算法的后验差比值是在1以内的,相对另外两条曲线而言,在高度上的值也是最小的。
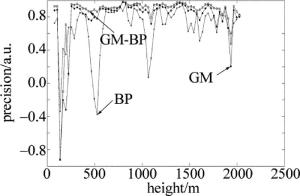
图 8中这3条曲线分别是水平风速在15:02:28~15:03:37时间段的3种控制算法的精度在高度上的变化情况。精度越接近1则反应控制效果越好。GM,BP和GM-BP这3种算法的精度基本上能保持在0.9左右,且在高度上GM-BP的精度是最稳定最接近1的。综合可知,平均相对误差、后验差比值和精度这3个验证质量控制效果的指标都体现了GM-BP对分廓线数据的质量控制效果是最好的。
-
使用BP神经网络修正灰色算法中的残差对雷达风廓线数据质量控制的研究。比较了GM(1, 1)算法、BP神经网络算法和BP-GM算法的数据控制效果。通过实时监测的风廓线数据进行计算分析,从风羽图效果来看,BP-GM算法更符合原始数据的风羽图,根据平均误差值、后验差比值及精度曲线也反映了BP-GM算法质量控制的优越性。试验数据表明, 使用BP-GM算法能有效地降低残差值,提高数据控制精度。BP-GM算法中使用多次BP神经网络修正灰色残差必然会造成计算耗时较多的情况,这也是该方法的最大不足之处。在后期工作还需要找到能快速训练神经网络以减少计算耗时的方法,以提高算法效率。

 Map
Map





 DownLoad:
DownLoad:






