Research of space-based photon counting laser detection for space debris

从第1颗人造地球卫星升空至今，人类在航天事业取得惊人成就的同时，也对空间环境产生了巨大影响，制造了大量空间碎片。截止到2015年9月，编目在轨的17265个地球轨道目标中，估计只有不到8%的目标是有效载荷，其余均为空间碎片^[1-2]。若空间碎片与在轨航天器发生碰撞，其平均撞击速率能达到10km/s，其中，尺寸1cm大小的空间碎片撞击释放出来的能量相当于一颗军用手榴弹^[3]。据估计，1cm以上的空间碎片已经超过40万个^[4]。空间碎片问题无疑使飞行器空间安全面临严峻的挑战。目前对于空间碎片的观测主要以地基观测为主，由于地基观测受天气、地域和观测时间等限制，在观测的时效性、有效性、覆盖性等方面难以满足要求，而且对于10cm以下空间小碎片，传统的地基雷达与光电探测手段测距误差一般达到了几百米^[5]。若要有效降低在轨航天器与空间碎片的碰撞概率，测距精度至少得达到米级或分米级^[6]。所以天地协同观测正受到学术界和业界广泛的重视。与地基观测相比，天基空间碎片观测发展相对滞后，理论、技术研究与实际应用还存在较大差距。

光子计数激光探测技术是一种新兴探测技术，它具有灵敏度高、精度高、能耗小、探测距离远等特点，是天基空间碎片探测极具技术潜力与应用价值的发展方向。2002年, 澳大利亚Stromlo激光测距站利用高能激光器完成了1250km处尺寸为15cm空间碎片的测距^[7]。2013年，奥地利Graz卫星激光测距站运用光子计数激光探测来进行空间碎片的探测与跟踪^[8]，在890km~2560km的距离范围内，探测跟踪到了横截面积最小可达到0.3m²的空间碎片。国内，中国科学院上海天文台、云南天文台等采用自主研制激光测距系统成功探测到了1m级空间碎片目标，精度达到1m左右^[9]。中国科学院上海技术物理研究所、上海光学精密机械研究所、南京理工大学、华东师范大学等单位开展了光子计数激光探测的研究，并取得了重要的研究成果。但是，从公开的文献中发现，对于空间高速运动目标的探测研究比较少。本文中针对10cm以下空间碎片探测与精密定轨的需求，基于目标已处于稳定指向跟踪状态，对基于光子计数的天基激光探测空间碎片进行了研究。

空间碎片属于非合作目标，当激光照射到空间碎片时，回波所包含的平均光子数可由激光雷达方程推导出。激光雷达方程能量形式^[10-11]如下所示：

式中，E_r为接收机所接收目标返回的能量；E_t为发射机激光能量；R为作用距离；Ω_t为发射波束的立体角；Ω_r为返回波束立体角；ρ为目标漫反射率；A_t为目标面积；A_c为接收机有效接收面积；η_t为发射波束单程传输系数；η_r为返回波束单程传输系数。由于激光发散角非常小，所以Ω_t可简化为Ω_t=πθ_t²/4，同时空间碎片在探测距离内主要是以点目标形式存在，所以Ω_r可简化为Ω_r=2π，再把N_r=E_rλ/(hc)和A_c=πD²/4代入(1)式，激光回波平均光子数N_r可由下式得出：

式中，θ_t为激光发散角；λ为激光波长；h为普朗克常量；c为光速；D为接收光学系统有效接收孔径。

以空间目标为探测对象的光子计数激光探测的噪声主要来源于太阳光干扰噪声和单光子探测器本身所自带的暗记数，这两种噪声是相互独立的两个随机过程^[12]。目前，性能良好的单光子探测器的暗计数率f_d可以降到1kHz以下。对于太阳光的干扰噪声，作如下分析。

假设空间碎片目标为朗伯体目标，太阳照射到空间碎片的辐照度为E_sun，在空间碎片表面发生漫反射，反射通量Φ=ρE_sunA_t。再假设反射为半球漫反射，可得反射后辐射强度为I=Φ/(2π)，接收机等效接收立体角为Ω=A_c/R²，最后可推得接收机接收的反射功率如下所示:

转化成单光子探测器上所产生的太阳光干扰噪声如下:

式中, Δk_λ为太阳辐射光谱在中心波段λ的某一谱段宽度范围Δλ时，其能量占全波段能量的比例。

对于本文中光子计数激光探测系统而言，激光脉冲输出信号是光强随时间变化的1维时间信号。激光源的时间分布特征直接影响探测距离的统计特性与探测精度等性能参量。本文中采用重尾函数^[13-14]来对激光源进行描述，如下式所示:

式中, P(t)为激光瞬时功率，A为功率幅值，τ为脉冲半宽度。对P(t)进行归一化处理，可得：

式中，∫₀^∞P₁(t)dt=1。

在本文设计中，采用的探测器是工作在盖革模式下雪崩二极管探测器(avalanche photodiode, APD)。盖革模式下的APD探测器，其在两端偏置电压高于雪崩电压状态下工作，当器件光敏面吸收一个光子后，将会产生一个自由载流子注入器件的倍增区，在反向偏压作用下，任何自由载流子的漂移都会触发雪崩电流，即单个光子引起雪崩效应，输出有效信号^[15-16]。

由统计光学理论可知，在激光直接探测中，经目标漫反射的激光回波信号服从负二项分布^[17-18]。在本文的光子计数激光探测中，由于回波的平均光子数远小于接收光学系统的散斑自由度，负二项分布可精确近似为泊松分布^[19]。由此可得出，在采样时间间隔ΔT内，回波信号产生k个光电子的概率p(k; ΔT)为：

式中，N_s(ΔT)为回波光子在采样时间间隔ΔT内产生的平均光电子数。

在盖革模式下的雪崩二极管的噪声主要来自背景噪声和暗电流，噪声产生的光电子也服从泊松分布^[14]，则产生的平均噪声光电子数为N_n，在采样时间间隔ΔT内产生k个光电子的概率为：

式中，N_{s, n}表示噪声产生的平均光电子数N_n与回波光子产生的平均光电子数N_s之和，N_{s, n}(ΔT)=N_s(ΔT)+N_n。

在本文的光子计数激光探测模型中，激光源的发射频率为时钟频率，两次激光发射之间都伴随一个相同的探测时间门，也叫距离门，将整个探测时间分为若干等距采样时间间隔ΔT，此时间间隔也为探测器时间最小分辨力。忽略激光回波的展宽效应，即认为激光的回波与输出信号在时间分布特性上只存在能量上的差异。在探测时间门内，在第j个采样时间间隔内产生的平均光电子数N_{s, n}(j)为：

本文中定义激光源时间特性分布参量T_e为激光输出信号强度从峰值下降到峰值的1/10处所对应的时刻，∫₀^T_eP₁(t)dt≈1。η为探测器量子效率, f_d为探测器暗计数率，t₀为每次回波光子在探测时间门内的抵达时刻。由于考虑了相对径向速率v，第i次发射激光的平均回波光子数N_r(i)及其t₀(i)由下两式给出:

式中，f为激光发射频率，R₀为目标起始距离。按照时间先后顺序依次对采样时间间隔内的光电子数进行探测。光电子数是以本采样时间间隔内的平均光电子数为参量，由泊松分布发生器产生的。若采样时间间隔内泊松分布发生器产生的光电子数N_{s, n}(ΔT)≥1，则表示在该时间间隔内探测到信号。由于探测器自身的原因，探测器存在一个时间抖动特性，一般抖动几百皮秒不等，而且这种探测到信号到输出信号之间的误差在时间上近似服从泊松分布^[20]。考虑时间抖动特性，当探测到信号后，需再进行一次以某抖动时间为参量的泊松分布生成，则在最后所对应的采样时间间隔信号计数器上加1。引入探测器的死时间参量，即探测器在这段时间不工作，一般为几十到几百纳秒不等。跳过死时间对应的采样时间间隔数为d，继续进行余下采样时间间隔探测，直到本次探测周期结束。最后形成信号计数值C与采样时间间隔的统计分布图。

当获得信号计数值C与采样时间间隔的统计分布图后，考虑到空间碎片速度可能很快，采样时间间隔ΔT很短，导致信号计数C在采样时间轴上分布离散。为了便于信号分析与目标鉴别，本文中提出，在满足一定距离误差的前提下，以相同的若干个采样时间间隔ΔT为一个信号计数统计单元u，得出一个统计单元的信号计数C，最后形成信号计数值C与统计单元u统计分布直方图。根据直方图进行目标鉴别与距离测量。假设允许的距离误差为b_s，一个采样时间间隔ΔT对应的探测距离为ΔR，则:

若对目标进行一次探测需发射N次激光，保证第1次与最后一次回波光子在探测门内产生的信号在一个统计单元内，则空间碎片的相对径向速度需满足下式:

对于盖革模式APD探测器来说，当至少有一个光电子产生时，则会产生探测信号。由于激光脉冲半宽度极短，在探测时间门内，回波光子被探测的概率p_d为:

由于在允许误差内回波光子数变化很小，p_d可认为不变。假设对目标发射N次激光，若存在同一统计单元信号计数值C>C_t(计数阈值)，则认为目标存在。目标的探测概率p_DT为:

在本文中，噪声主要来自太阳光噪声与暗计数噪声，则一个统计单元u由噪声产生信号的概率p_n为:

若死时间很长，与探测时间门相当，即在探测时间门内只能探测到一次信号。则在探测时间门内第m个统计单元探测到信号的概率p_l(m)为：

则第m个统计单元信号计数值C>C_t的概率p_{l, 2}(m)为：

探测一次目标，其虚警概率p_FA为：

式中，M为一个探测门总统计单元数。

若死时间较短，即在探测时间内探测到一次信号后，还能继续探测信号，则在探测时间门内第m个统计单元探测到信号的概率p_s(m)为：

式中，d_u为死时间对应统计单元数。第m个统计单元信号计数值C>C_t的概率p_{s, 2}(m)为：

探测一次目标，其虚警概率p_FA为：

作用距离R的测量是利用光子在探测器与目标之间飞行时间来测量的。设光子的飞行时间为t_f，则目标距离R=ct_f/2。本文中把光子飞行时间t_f的测量分为粗测与精测两部分，两部分分别对应不同的测量尺度。假设激光的发射周期为T，则飞行时间中粗测部分对应的测量尺度为T，精测部分的测量尺度为探测时间门内的采样时间间隔ΔT，也可称为距离栅格。飞行时间的测量基本原理如图 1所示。其中t_s为探测门的起始时间，nT为飞行时间的粗测部分，Δt为飞行时间的精测部分，则光子的飞行时间t_f=nT+Δt。

Figure 1.  Time-of-flight measurement principle

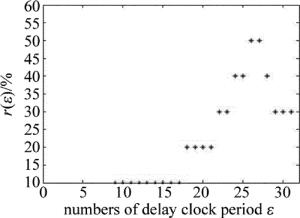
本文中基于时间延迟的相关法来进行粗测。每个探测时间门都有对应的时钟周期信号计数器，记录对应的时钟周期是否存在过信号。若在此距离门内产生过信号，则在对应的时间周期的计数器记1，即C(j)=0或1, j为T的正整数倍。假设一次探测发射N次激光，激光的发射函数可表示为S(i)=1, i=1T, 2T, …, NT。则时间延迟相关度r可由下式计算:

式中，ε为相关延迟时钟周期数，其范围可根据任务要求或先验知识提前给定。在一定延迟时间范围内，r(ε)最大值所对应的ε, 即为粗测部分nT。

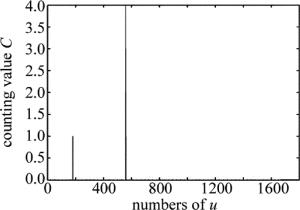
精测部分，Δt=t_s+(m-1)u+0.5u。探测门起始时间t_s一般提前已设定，所以只需要测定统计单元数m。依据信号计数值C与统计单元分布直方图，判定是否存在目标，并选取信号计数值最大的所对应的统计单元为测定的m。

为了验证光子激光探测技术对于空间碎片探测的有效性，并评估其工作性能，本文中利用设计的探测模型在MATLAB软件上进行了一系列仿真实验，仿真流程如图 2所示。

Figure 2.  Flow chart of simulation

假设目标起始相距探测器200km，空间碎片直径为10cm，以1064nm窄脉冲激光器为光源，发射峰值功率为70mW，接收孔径为600mm，束散角为0.1mrad，发射波与回波单程传输系数为0.95，由(2)式可算出平均回波光子数约为1.12个，回波光子探测概率p_d= 42.89%。探测背景为深空环境，空间碎片处于顺光照射下。由(4)式计算近地轨道目标反射太阳光噪声f_b=9.5kHz，暗计数噪声f_d=1kHz。假设允许误差为0.9m, 激光发射频率f=20kHz，发射次数N=10，则对应的速率边界为2km/s，为了保证目标的探测概率为95%以上，则设定C=1，对应的目标探测概率为96.86%，虚警概率为8.42×10^－5。当目标相对径向速率v=2km/s时，其探测结果的精测部分与粗侧部分分别如图 3和图 4所示。

Figure 3.  Results of precision measurement

Figure 4.  Results of rough measurement

由图 3信号计数值C与u分布直方图可知，存在某一统计单元的C>C_t, 则说明目标存在，与仿真设定相符。由图 4中距离的粗测部分可知，最大r(ε)= 50%，ε为26T和27T，实际仿真设定ε=26T，误差为1T。由于目前地基测距误差可在1km以内，而本文中的激光发射周期(时钟周期)T=50μs，一个时钟周期对应距离7.5km，所以在天地协同观测的背景下，粗测误差可消除。假设没有任何先验知识，可通过多次探测，依据之前的探测结果，改变发射频率，从而改变粗测尺度，进而消除粗测误差。关于光子计数激光探测，一般认为距离的测量误差主要来自于精测部分。再由图 3可知，第558个统计单元的C=4，则精测部分的m=558，距离误差为48.33cm。改变目标相对径向速率，其探测结果如表 1所示。在速率边界内(含2km/s)，平均测距误差34.72cm，误差结果在允许范围内，可以有效降低航天器碰撞概率。当目标速率大于速率边界时，探测器仍能发现目标，但是其测距误差不一定在允许范围内。当考虑速率边界时，是要求第1次与最后一次的回波光子落在探测门内的最大时间差在一个u内，而在实际情况中，只要大于C_t次的回波光子落在一个u内，就可以发现目标了。如果把(13)式中(N-1)换成C_t，速率边界将变为18km/s，称这个速率边界为极限速率，超过这个极限速率理论上将不可能发现目标。当目标速率介于2km/s与18km/s之间时，将无法保证回波光子落在同一个u内，从而无法保证误差在允许范围内。而且，此时目标的实际探测概率将偏离(15)式给出的探测概率。综合考虑，本文中速率边界将由(13)式给出，在此速率边界内，探测概率可由(15)式反映，同时能保证误差在允许范围内。

以空间碎片引发的空间环境问题为背景，通过利用光子计数激光探测技术灵敏度高、精度高、能耗小、探测距离远等优点，从原理上对天基光子计数激光探测空间碎片展开了研究，并以此为基础建立了考虑相对径向速率的空间碎片探测模型以及设计了一种光子计数激光探测空间碎片的方法，并进行了相关仿真试验。在起始距离为200km、目标尺寸为10cm、相对径向速率从0.5km/s到2km/s、并伴有太阳光噪声和暗计数噪声的空间碎片探测试验中，以现有激光测距硬件能力为基础，采用光子探测技术，探测器能有效发现10cm空间碎片目标，平均距离误差为34.72cm，测距精度能有效降低在轨飞行器碰撞概率。下一步研究将会对相关边界条件进行深入研究，优化探测条件，提升探测性能。