Advanced Search

ISSN 1001-3806 CN 51-1125/TN Map

Volume 41 Issue 2
Mar.  2017
Article Contents
Turn off MathJax
Article Navigation >  LASER TECHNOLOGY  > 2017 >  41(2): 296-301

Citation:
shu

Design of fisheye lens of omnidirectional gaze photoelectric imaging systems

  • 1.

    School of Instrumentation Science and Opto-electroncis Engineering, Beihang University, Beijing 100191, China

  • 2.

    Precision Opto-mechatronics Technology Key Laboratory of Education Ministry, Beihang University, Beijing 100191, China

  • Corresponding author: NIU Yanxiong, niuyx@buaa.edu.cn ; 
  • Received Date: 2016-03-07
    Accepted Date: 2016-03-16
  • In order to achieve imaging, detection and alarm of hemisphere space target by photoelectric imaging system, based on large field imaging and aberration theory, fisheye lens of optical system was theoretically analyzed and simulated by the scaling laws. The barrel distortion and stop coma were used to increase the illumination uniformity of image plane. The system axis aberration decreased by means of ray aiming iteration. Imaging quality of the system was evaluated and analyzed multiply. Distortion correction model of imaging lens was derived. The results show that, in visible spectrum, fisheye lens of excellent imaging quality is gotten, with the CCD effective size of 8.446mm×7.042mm, effective pixels of 2448×2050, entire field of view of 180°, focal length of 2.24mm, relative aperture of 1:2.8, image plane illumination uniformity of over 90%, and mean square root radius value of diffuse spot diagram of less than 1/2 pixel. The modulation transfer function with spatial frequency of 145lp/mm is greater than 0.4. The omnidirectional gaze photoelectric imaging system can realize the real-time detection of hemisphere space target.
  • 加载中
  • [1]

    LIANG J W, LUO Ch H, YANG M. Optical design of fish-eye lens used for monitoring system[J]. Optical Technique, 2011, 37(6):691-694(in Chinese).
    [2]

    XU Y N, ZHAO Y, JIN Ch F, et al. Design of the imaging satellite-borne laser warning system[J]. Infrared and Laser Engineering, 2006, 35(s3):357-360(in Chinese).
    [3]

    MA W P. Discussion on staring imager for LEO earth observation satellite[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(4):17-21(in Chinese).
    [4]

    LIU Zh J, CHEN W. Space applications of staring imaging technology with area FPA[J]. Infrared and Laser Engineering, 2006, 35(5):541-545(in Chinese).
    [5]

    ZHANG X T, AN Zh Y. Fish-eye lens design of hazard avoidance cameras for mars exploration[J]. Science Technology and Engineering, 2012, 12(34):9333-9336(in Chinese).
    [6]

    ZHENG W. Based on the Q-type aspheric technology of low edge image compression panoramic lens design[D]. Fuzhou: College of Photonic and Electronic Engineering Fujian Normal University, 2013: 4-5(in Chinese).
    [7]

    THIBAULT S, PARENT J, ZHANG H, et al. Design, fabrication and test of miniature plastic panomorph lenses with 180° field of view[J].Proceedings of the SPIE, 2014, 9293:92931N. doi: 10.1117/12.2074334
    [8]

    SAMY A M, GAO Zh Sh. Fovea-stereographic:a projection function for ultra-wide-angle cameras[J]. Optical Engineering, 2015, 54(4):045104. doi: 10.1117/1.OE.54.4.045104
    [9]

    ZHANG B L, LI D, ZHANG Sh J, et al. Design of aspheric fisheye lens and study of distortion correction algorithms[J]. Acta Optica Sinica, 2014, 34(12):1222001(in Chinese). doi: 10.3788/AOS
    [10]

    CHEN Sh C, LIN F. Research and design of super short-focus panoramic fish-eye lens[J]. Opto-Electronic Engineering, 2012, 39(2):48-52(in Chinese).
    [11]

    WANG Y Zh. Fisheye lens optics[M]. Beijing:Science Press, 2006:14(in Chinese).
    [12]

    LI H Zh, ZHANG Zh D, LIU X Y, et al. Optical design of a wide spectral fish-eye lens[J]. Acta Photonica Sinica, 2012, 41(11):1312-1316(in Chinese). doi: 10.3788/gzxb
    [13]

    XUE Q Sh, CHEN W. Optical system design of space-based UV panoramic imager[J]. Infrared and Laser Engineering, 2014, 43(2):517-522(in Chinese).
    [14]

    MILTON L. Lens design[M].4th ed. Beijing:China Machine Press, 2012:101-103(in Chinese).
  • 加载中
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索

Figures(12) / Tables(5)

Get Citation
PDF
XML

Article views(6490) PDF downloads(342) Cited by()

Proportional views

Design of fisheye lens of omnidirectional gaze photoelectric imaging systems

    Corresponding author: NIU Yanxiong, niuyx@buaa.edu.cn; 
  • 1. School of Instrumentation Science and Opto-electroncis Engineering, Beihang University, Beijing 100191, China
  • 2. Precision Opto-mechatronics Technology Key Laboratory of Education Ministry, Beihang University, Beijing 100191, China
  • Received Date: 2016-03-07
  • Accepted Date: 2016-03-16
  • Available Online: 2017-03-25

Abstract: In order to achieve imaging, detection and alarm of hemisphere space target by photoelectric imaging system, based on large field imaging and aberration theory, fisheye lens of optical system was theoretically analyzed and simulated by the scaling laws. The barrel distortion and stop coma were used to increase the illumination uniformity of image plane. The system axis aberration decreased by means of ray aiming iteration. Imaging quality of the system was evaluated and analyzed multiply. Distortion correction model of imaging lens was derived. The results show that, in visible spectrum, fisheye lens of excellent imaging quality is gotten, with the CCD effective size of 8.446mm×7.042mm, effective pixels of 2448×2050, entire field of view of 180°, focal length of 2.24mm, relative aperture of 1:2.8, image plane illumination uniformity of over 90%, and mean square root radius value of diffuse spot diagram of less than 1/2 pixel. The modulation transfer function with spatial frequency of 145lp/mm is greater than 0.4. The omnidirectional gaze photoelectric imaging system can realize the real-time detection of hemisphere space target.

    HTML

引言

  • 全向凝视光电成像系统视场达180°, 可实时探测半空域的目标信息, 在安防监控、激光告警、航天遥感和空间探测等领域都有十分广阔的应用前景[1-5]。鱼眼镜头是全向凝视光电成像系统的重要组成部分, 模仿鱼在水里能够凝视水面上近乎半空域景物的特性制成, 与旋转扫描式镜头和多镜头图像拼接式系统相比, 鱼眼镜头能够更加全面、快捷地获取全景信息。但是, 由于具有超大视场, 鱼眼镜头边缘分辨率比较低, 而许多重要的成像领域要求全视场有较高分辨率。所以, 大口径、高分辨率鱼眼镜头的研究具有重要意义。目前, 国外富士能首次研发了用于500万像素图像传感器的鱼眼镜头, 视场为185°; 美国火星探测器的避险相机使用了鱼眼镜头[6]; Immer Vision公司发布了全长仅3.8mm百万鱼眼[7]。国内GAO等人设计了凹球面超广角鱼眼相机[8]; ZHANG等人设计的车载鱼眼镜头[9], 像素大小为100万; CHEN等人研究的超短焦鱼眼镜头[10], 有效像素为300多万; ZHANG等人研制高清全景摄像机, 每帧画面达到2500万像素。可见, 高分辨率全向凝视光电成像系统鱼眼镜头有较大的发展前景。

    本文中以光学设计及大视场成像理论为基础, 采用缩放法对全向凝视光电成像系统鱼眼镜头进行设计优化, 利用桶形畸变及光阑彗差增大像面照度的均匀性, 通过光线迭代瞄准程序减小轴外像差, 对透镜的成像质量进行多次评价与分析, 并推导了透镜的畸变校正模型。探测器采用SONY公司11mm对角线CCD, 有效像素为2448×2050, 工作波段为可见光, 鱼眼镜头焦距为2.24mm, 相对孔径为1:2.8, 光电成像系统视场达180°, 像面照度均匀性达到90%以上, 光学传递函数在145lp/mm空间频率处大于0.4, 成像质量良好。

1.   全向凝视光电成像系统

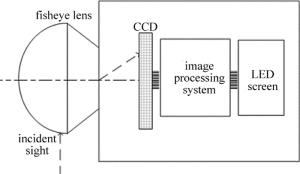
  • 全向凝视光电成像系统可实时探测半空域的目标信息, 系统主要由鱼眼镜头、CCD图像传感器、图像采集处理系统和显示器组成, 其结构如图 1所示。鱼眼镜头把半空域的目标光信息压缩成像在CCD图像传感器上, 图像传感器把目标光信号转换为携带图像信息的电信号, 图像采集处理系统对图像传感器输出的电信号进行采集和存储, 由于鱼眼镜头拍摄的全向凝视图像往往存在较大的形变, 不符合人眼的观察习惯, 所以除了正常的图像处理程序外, 还须进行图像的畸变算法校正, 最后在显示器上输出正常的半空域图像信息。

    Figure 1.  Schematic of omnidirectional gaze photoelectric imaging system

2.   鱼眼镜头的设计

  • 在全向凝视光电成像系统中, 为了实现半空域探测, 须使用圆周鱼眼镜头, 即镜头所成画面中间呈圆球形, 四角为黑色, 在各个方向视场均达180°。

    • 2.1.   设计方法

  • 由于视场比较大, 鱼眼镜头的设计难点主要见下。

    • 2.1.1.   像面照度不均匀

  • 若按一般成像系统cos4ω'规律衰减, 则当边缘像方视场角ω'=60°时, 它的像面照度仅为中心视场照度的6.25%, 不满足成像要求, 因此必须提高边缘视场像面照度, 即提高像面照度均匀性。本文中主要通过3种方法来提高像面照度均匀性。

    (1) 采用反远距型结构[11], 工作距离l'大于焦距f', 如图 2所示。F'和H'分别为系统像方焦点和像方主点, 镜头主要由前后两个光组构成, 前方光组的光焦度φ1为负, 轴外光线经过前组透镜的发散之后, 与光轴的夹角明显变小, 从而增大镜头视场, 后方光组的光焦度φ2为正, 可使得像方视场角减小, 有效减缓边缘照度下降。同时, 这种结构可以获得较大的工作距离。

    Figure 2.  Basic structure of the inverted telephoto lens

    (2) 人为引入大量桶形畸变, 使边缘视场成像光线被压缩, 从而提高像面照度均匀性。目前, 鱼眼镜头的主要压缩方式有等距离投影、等立体角投影、体式投影和正交投影。在全向凝视光电成像系统中, 为了观测方便, 能直接从图像提取出物空间的角坐标, 简化计算[12], 本文中选择等距离投影成像, 其公式为:

    式中, f'为鱼眼镜头的焦距, ω为系统视场角, y'为像面高度, 可见物方视场角与像高成正比例关系, 方便演算。

    (3) 利用光阑彗差, 它是孔径光阑经前面光组成像时, 与光轴正交方向上的入瞳像差。对于大相对孔径和大视场角的系统来说, 随着视场角的增大, 入瞳的位置将会从物镜内部向物镜前方移动, 并且入瞳尺寸会有所增大。由于光阑彗差的存在, 经过近轴入瞳边缘的轴外光线, 在孔径光阑面上的投射高度几何量小于孔径光阑直径。若保证轴外光束充满孔径光阑, 则轴外物点实际成像光束在近轴入瞳面上的投射宽度大于轴上光束宽度。此时实际像面照度公式为:

    式中, EM'代表轴外像点的光照度, E'代表轴上像点的光照度, Sω, SO分别为入瞳面上轴外光束截面积和轴上光束截面积[13]。可知, 利用光阑彗差产生的像差渐晕可大大提高像面照度均匀性。

    • 2.1.2.   轴外像差难以消除

  • 鱼眼镜头是超大视场光学系统, 轴外像差比较大, 不仅会降低系统的成像质量, 还会严重影响光学系统的分辨率, 极大限制了鱼眼镜头的应用。在优化设计时, 采用光线逐步尝试拟合的方法来追踪鱼眼镜头入瞳位置, 使轴外边缘视场的主光线能够通过入瞳中心, 来减小轴外像差, 在光学设计软件ZEMAX的General选项中打开光线校准功能, 用光线校准时, 每个光线追迹是迭代执行的, 同时调整程序以便各视场光线能通过光阑面上正确的位置, 以此来消除像差。

    • 2.2.   设计参量确定

  • 由上述可知, 本次鱼眼镜头设计按y'=f'ω投影成像公式计算, 由物像关系可得鱼眼镜头焦距f', 计算公式为:

    式中, r为CCD探测面的有效半径。文中选用的CCD探测器是由SONY公司所生产的ICL-B2520C, 有效像面尺寸为8.446mm×7.042mm, CCD对角线长度为11mm, 有效像素为2448×2050, 像元尺寸为3.45μm×3.45μm。CCD上最大成像圆周半径是:

    系统视场角ω=90°, 由(3)式可得:

    CCD的像素分辨率为θ0:

    光学系统的分辨率为θ1:

    式中, 成像主波长λ=587.6nm, D是鱼眼镜头的入瞳直径。考虑到加工误差对光学系统分辨率的影响, 设计时应使光学系统分辨率大于CCD像素分辨率, 才能更好地与CCD相匹配。为保证全向凝视光电成像系统的探测能力, 取鱼眼镜头光圈数F=2.8, 系统工作波长为可见光波段。可得鱼眼镜头的设计参量, 如表 1所示。

    parameter value
    pixel size 6μm×6μm
    wavelength visible spectrum
    focal length 2.24mm
    F /# 2.8
    field of view 180°
    relative illumination > 0.8%
    MTF of all fields(145lp/mm) > 0.3

    Table 1.  Specifications of design

3.   设计过程及结果分析

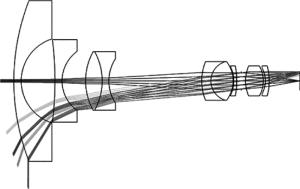
  • 由以上技术参量, 选择大量符合的初始结构, 经过ZEMAX软件进行初步优化, 仔细衡量各个结构的优化潜力, 最终选择视场角为170°, 相对孔径1:2.8的超广角镜头为初始结构[14], 在此基础上利用ZEMAX和CODEV进行优化设计。首先进行焦距逐步缩放, 并且增大透镜视场至180°, 在仿真软件中对镜片半径、厚度及光线入射位置等进行控制, 在优化函数里加入REAY, CTGT, CVVA, TTHI等操作数对透镜结构不断调整优化, 主要考察像面相对照度、轴外像差大小及光学传递函数曲线值。同时, 考虑镜头的加工工艺以及制作成本, 第1片透镜属于负弯月形透镜, 加工难度大, 采用肖特玻璃库玻璃N-BK7(折射率为1.52, 阿贝数为64.2)能够减少透镜的加工成本。最终得到鱼眼镜头的2维光路, 如图 3所示, 表 2中是镜头数据结果。镜头焦距2.24mm, 视场180°, 相对孔径1:2.8, 最大光学口径Ø48mm, 后截距为9mm, 总长约85mm, 系统结构简单, 能够探测半空域目标信息, 满足全向凝视光电成像系统的应用需求。

    Figure 3.  2-D optical path diagram of fisheye lens

    surface number radius/mm thickness/mm reference index(glass) Abbe number
    object infinity infinity
    lens 1 66.143
    13.211    		 2.2
    10.036    		 1.52(N-BK7) 64.2
    lens 2 -103.504
    10.988    		 2.119
    6.997    		 1.59(N-SK5) 61.3
    lens 3 18.180 4.938 1.72(SF1) 29.5
    lens 4 -18.265
    12.247    		 1.994
    27.621    		 1.69(N-LAK9) 54.7
    lens 5 15.187 2.732 1.69(N-LAK9) 54.7
    lens 6 6.036
    -9.666    		 6.609
    0.214    		 1.55(N-PSK3) 63.5
    lens 7 -9.622
    -23.548    		 0.874
    1.311    		 1.72(SF1) 29.5
    stop surface infinity 1.311
    lens 8 11.316
    -9.228    		 5.279
    0.597    		 1.55(N-PSK3) 63.5
    lens 9 -8.072
    -16.706    		 1.176
    9.080    		 1.72(SF1) 29.5
    image surface infinity

    Table 2.  Design data of fisheye lens

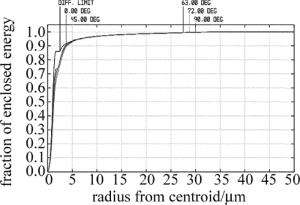
    图 4是各视场在像面上的点列图分布图, 它可以更加直观地看到成像光斑特性。可得出系统成像的光斑最大均方根(root mean square radius, RMS)半径值为1.631μm, 小于探测器像元尺寸的一半, 可以很好地避免光电探测器像面辉光现象。图 5是各个视场的能量集中度分布曲线, 横坐标是像斑直径, 纵坐标是能量集中度。由表 3可看出, 85%的能量集中在半径为3.2μm的区域内, 小于一个像元尺寸。

    Figure 4.  Spot diagram of system

    Figure 5.  Distribution curve of energy concentration

    field 0° 45° 63° 72° 90°
    50% energy concentration range 1.2 1.3 1.4 1.4 1.3
    85% energy concentration range 2.9 3 3 3.1 3.2
    90% energy concentration range 3.5 4 4 4 4

    Table 3.  Distribution value of energy concentration

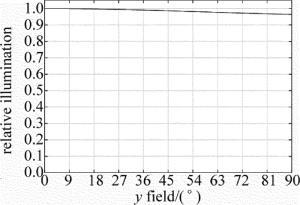
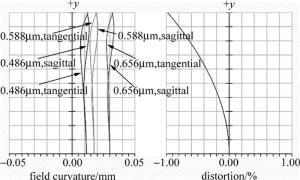
    文中设计的全向凝视光电成像光学系统通过引入大量桶形畸变和光阑彗差产生的像差渐晕来提高像面照度均匀性。图 6是光学系统的相对照度曲线。由图可见, 各个视场的相对照度曲线值达到0.9以上, 这表明轴外物体成像光线很好地参与了成像, 像面光照度均匀性良好。图 7为场曲与f'tanθ畸变曲线。可看出系统场曲低于0.05mm, 此外, 为了提高系统的边缘像面相对照度, 保证从半球物空间获取图像信息, 系统引入了很大的桶形畸变, 系统边缘视场最大畸变为-97.8%。畸变虽然不影响成像清晰度, 但是, 畸变对图像形变有很大影响, 这样的图像不符合人眼的观察习惯, 所以, 全向凝视光电成像系统还需要图像采集处理系统对图像进行后期算法校正。

    Figure 6.  Relative illumination

    Figure 7.  Figure of field curvature and f'tanθ distortion

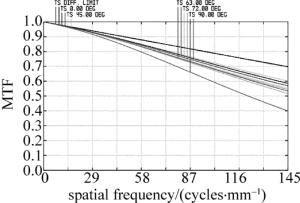
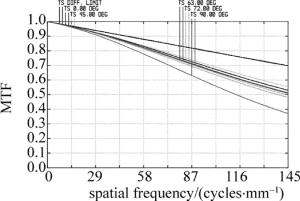
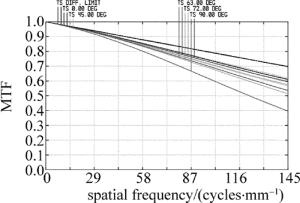
    对于成像镜头来说, 最适合利用光学传递函数来进行像质评价。光学传递函数既与光学系统的像差有关, 又与光学系统的衍射效果有关, 用它评价光学系统的成像质量, 客观可靠。图 8是镜头在20℃温度下的光学调制传递函数(modulation transfer function, MTF)曲线, 图中横轴表示像面上的空间频率, 纵轴表示光学传递函数值。设计所选用CCD像元尺寸3.45μm, 它所对应的最大空间频率为145lp/mm, 此时, 90%视场的MTF值均在0.5以上, 仅有边缘90°子午视场曲线值为0.4, 符合设计指标要求。考虑到全向凝视光电成像系统军事方面的应用, 对镜头在不同温度下MTF进行仿真分析, 利用光学软件ZEMAX, 改变环境温度参量, 图 9、图 10分别为系统在-50℃, 70℃温度下的调制传递函数。可见当环境温度极大降低时, 系统MTF数值与常温相比有约0.03的降低, 变化很小, 而当温度升高时, MTF曲线几乎没有变化。表明镜头温度特性良好。

    Figure 8.  Relationship between MTF and spatial frequency at 20℃

    Figure 9.  Relationship between MTF and spatial frequency at-50℃

    Figure 10.  Relationship between MTF and spatial frequency at 70℃

    利用CODEV软件的2维图像仿真功能, 对上述鱼眼镜头进行成像仿真模拟, 图 11为仿真成像对比图。由图可以看出, 像面光照度均匀性良好, 光学系统成像清晰但却存在很大的桶形畸变, 图像边缘光线被大量压缩向像面中心。为了对影响透镜成像质量的像差进行具体分析, 在ZEMAX软件中计算出透镜系统的初级seidel像差系数, 如表 4所示。初级彗差系数S2=-0.161835, 初级畸变系数S5=9.09×106, 与畸变相比, 其它像差对系统成像质量的影响很小。畸变并不影响系统的光学分辨率, 所以可以在不损失像面分辨率的情况下用软件算法进行校正, 即把带畸变的图像模型转换为线性小孔成像模型。由ZEMAX的畸变曲线得出透镜各个视场角对应的像面实际高度, 利用MATLAB曲线拟合工具箱推导出像面实际像高r'与视场角θ的正弦求和函数公式, 模型拟合精确度为1, 均方根误差为0.0016, 拟合模型符合镜头畸变情况:

    Figure 11.  Comparison

    sphere aberration S1 coma aberration S2 astigmatism aberration S3 field-curve aberration S4 distortion aberration S5 longitudinal chromatic aberration lateral chromatic aberration
    0.00228 -0.161835 68.9144 64.5018 9.09×106 -0.00057 -0.04616

    Table 4.  First order of seidel coefficients

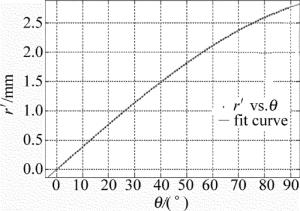
    拟合模型的系数a, b, c的数值如表 5所示。图 12是模型拟合曲线图。而线性小孔成像模型为r=f'tanθ, 可以推出转换模型公式(9)式, 即可得到与畸变图像坐标r'一一对应的无畸变的图像坐标r, 从而完成图像校正。

    Figure 12.  Relationship between real image height and field of view

    coefficient a b c
    first order 3.029 0.0129 -0.0001979

    Table 5.  Coefficients of sine sum

4.   结论

  • 以大视场成像理论和像差理论为基础, 采用缩放法设计了一款反远距型结构的高分辨率鱼眼透镜, 能够提供较大的工作距离, 采用缩放法对全向凝视光电成像系统鱼眼镜头进行设计优化, 利用桶形畸变及光阑彗差增大像面照度的均匀性, 镜头焦距为2.24mm, 视场为180°, 并对镜头的成像特性及温度特性进行了评价与分析, 推导出了镜头的畸变校正模型。

Reference (14)

Catalog

    Copyright © Laser Technology. 蜀ICP备10038222号-1

    Address：No. 7, Section 4, Renmin South Road, Chengdu, Sichuan Province, China Postal Code：610041  Telephone：028-68011091/68011046  Email： jgjs@vip.163.com,  jgjs@sina.com

    Supported by: Beijing Renhe Information Technology Co. Ltd  support: info@rhhz.net

    /

    DownLoad:  Full-Size Img  PowerPoint
    Return
    Return