Applications of random sample consistency algorithm on laser spectroscopy

自20世纪80年代以来，随着经济的发展，全球环境问题日益突出，如温室效应、臭氧层破坏、雾霾、酸雨和光化学烟雾等，严重威胁着全球人类的生存和发展。发展大气污染物的监测技术，为环境污染的监控、治理以及环境科学问题的研究提供必要的实验数据和理论支持，已成为环境科学家们的首要任务。可调谐半导体激光吸收光谱(tunable diode laser absorption spectroscopy, TDLAS)作为一种新型的非接触式气体浓度诊断技术，具有高分辨率和响应速度快等特点，从而被广泛地应用大气温室气体及其它大气痕量气体的测量研究^[1-2]。TDLAS的测量方法主要基于朗伯-比尔定律，通过检测气体分子对特定波长的激光吸收而产生的光强衰减量，结合一定的算法模型和已知实验参量，即可直接反演出被测分子的浓度、温度和速度等信息。该方法相对简单，但易受噪声影响，测量精度和灵敏度有限。鉴于半导体激光器的可调谐特性，1981年, REID和LABRIE提出将波长调制技术应用于TDLAS^[3]，利用高频正弦信号叠加到低频激光波长扫描信号中调制激光器, 使得探测器探测到信号含有高频的谐波分量, 进而通过锁相放大器进行提取，能有效地抑制1/f噪声，从而实现更高精确度的测量。

波长调制光谱中二次谐波探测技术灵敏度较高，因而被广泛地用于气体浓度的测量，但该技术首先需要对系统进行标定后才能反演出被测样品的浓度信息^[4-5]。鉴于二次谐波信号与样品浓度之间的线性关系，目前采用的反演算法主要包括二次谐波信号峰值比值法和二次谐波信号整个线型轮廓线性回归分析法^[6]。前者采用样品信号和参考信号之间单个峰值的比值，在低浓度的情况下(吸收信号较弱，噪声干扰明显)测量误差较大。后者利用整个二次谐波信号的有效吸收线型，结合最小二乘法拟合算法(least square method, LSM)^[7-8], 反演数据点增加，可有效降低测量误差，但是仍然受到非相关的噪声影响，导致拟合结果有所偏差。

本文中针对当前波长调制光谱技术中信号处理方法存在的问题，提出了一种改进的反演气体浓度算法，结合随机抽样一致性(random sample consensus, RANSAC)算法，用于高精度的大气痕量气体测量。首先介绍了相关算法的基本理论，通过将自行建立的RANSAC算法模型应用到理论模拟和实验测量的数据处理中，对该算法模型的可靠性进行系统地评估。

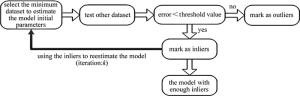
RANSAC算法最早由FISCHLER和BOLLES于1981年提出^[9]，作为一种迭代方法，用来在一组包含离群的被观测数据中估算出数学模型的参量。其主要原理是：输入一组实验数据，通过迭代反复选择数据中的一组随机子集(局内点)，排除噪声(局外点)，给出一个模型，最大概率的适用于局内点, 算法流程见图 1^[10-11]。

Figure 1.  The flowchart of RANSAC algorithm

RANSAC算法计算过程中，要确定的参量有判断为内点的阈值t、使得模型足够合理的内点数目d，被重复执行上述流程的次数k(迭代次数)可以从理论结果推断出。从估计模型参量时，用p表示在迭代过程中从数据集内随机选取出的点均为局内点的概率，用w表示每次从数据集中选取一个局内点的概率：w=局内点的数目/数据集的数目。

假设估计模型需要选定n个点，wⁿ是所有n个点均为局内点的概率；(1-wⁿ)是n个点中至少有一个点为局外点的概率，此时表明从数据集中估计出了一个不好的模型。(1-wⁿ)^k表示算法永远都不会选择到n个点均为局内点的概率，它和(1-p)相同，即：1-p=(1-wⁿ)^k。两边取对数，即得到迭代次数:

阈值t的选取很重要，直接影响内点外点的判断^[12]。因为在判断有效点的时候，若选取的t较小，则会放弃应该选择的有效点；而选取的t较大，则可能将异常点或误差点误判为有效点。针对该问题，本文中采用绝对中位差(median absolute deviation, MAD)D_MAD来估计数据的方差。假设选取的数据子集为y_i，则其表达式为：

式中，median为求数组的中值函数，∣·∣为求绝对值符号，i和j分别为数据子集位置。阈值t取实验数据的绝对中位差，再用模型去测试其它实验数据，若数据点到直线的距离小于t时，此点被认为是内点，反之则为外点。

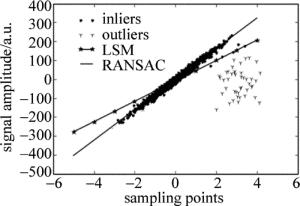
为验证两种算法的可靠性和稳健性，对同一组含有相同误差和异常点的数据进行模拟，当数据(inliers)中不添加异常点和添加50个异常点(outliers)时，LSM和RANSAC算法的拟合结果如图 2所示。

Figure 2.  Fitness results of the same data sets by applying LSM and RANSAC

结果显示, 最小二乘法对异常值较敏感，当实验数据中出现异常点时，最小二乘法拟合的直线极大地偏离原直线；而RANSAC则可有效地排除异常点的影响，拟合结果非常接近原模型，具有较好的稳健性。相比于最小二乘法，RANSAC算法在计算参量的迭代次数没有上限，其优点是它能鲁棒性地估计模型参量，即使是对于存在一定显著数量的异常值的数据集，也可以高精度的估计参量，因而被广泛地应用于图像处理。实际应用中，通过最佳化RANSAC模型参量可找到最大内点集^[13-15]，减小误差概况概率，提高数据处理的精确度。

本文中首先通过采用Python程序语言自行编程对波长调制二次谐波信号进行仿真研究。假设不含噪声的体积分数为10^-7的甲醛二次谐波信号为参考信号X(信号幅值为相对值)，体积分数为2×10^-7的二次谐波信号为待分析信号Y，并通过对待分析信号Y添加不同幅值A的噪声(部分信号如图 3a~图 3c所示)，进而对以上两种线性拟合模型进行评估。以图 3a~图 3c仿真二次谐波信号(横坐标为采样点数，无单位)中每个X信号为横坐标，Y信号为纵坐标，画出的图形及相应线性拟合结果分别展示在对应的图 3d~图 3f中，最终拟合结果统计如表 1所示。从表 1可以看出，对具有较高信噪比(signal-to-noise ratio, SNR)R_SNR的谐波信号进行线性拟合，两种算法的拟合结果具有很好的一致性；随着噪声的增加，对具有较低信噪比的二次谐波信号进行线性拟合时，RANSAC算法明显比LSM更具有优越性，拟合结果的线性相关度R²要明显高于LSM, 且拟合的比值(slope)(即线性拟合的斜率，Y与X的比值)更接近真实值2.0。

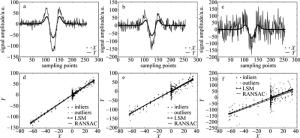
Figure 3.  a~c—the simulated second harmonic signal of formaldehyde with noise level A=10, 20, 50, respectively e~f—the corresponding fitted results by using LSM and RANSAC algorithms, respectively

为了进一步对两种拟合算法进行评估，将两种拟合模型应用到实验中记录的大气甲醛二次谐波信号处理中，实验测量系统如参考文献[16]中所述。大气中甲醛含量极低，因此，实验中测量的光谱信号质量较差。实验上获得二次谐波信号I_{2, f}与气体分子浓度C之间满足以下关系^[17]：

式中，I₀为激光初始光强，α为分子吸收系数，L为有效吸收光程。因此，通过将未知浓度的样品信号与已知参考样品的信号进行对比分析，即可消除初始光强的影响，从而获得未知样品的浓度信息。本文中主要是通过已知浓度的甲醛信号，对相关算法的可靠性进行初步的评估。图 4a是不同甲醛体积分数的两个二次谐波信号(signal_1:42×10^－9；signal_2:35×10^－9)，信号基线部分受到采集系统噪声的严重干扰。类似于图 3处理方法，以signal_2的数据点为横坐标和signal_1的数据点为纵坐标时，给出如图 4b中符号“·”所示的依赖关系(包含inliers和outliers)，图中符号“-”描述的分别为LSM和RANSAC算法线性拟合的结果。由此图可见，LSM算法处理的对象为整个数据点集(inliers+outliers), 而RANSAC算法通过排除含有噪声干扰的数据点(outliers)，只对有效数据(inliers)进行拟合分析，从而使得拟合结果的可靠性得到显著提高。图 5a为甲醛体积分数为35×10^－9不变的情况下，长时间连续测量二次谐波信号时不同时刻下选取的两个二次谐波信号(signal_2和signal_3)，由于受系统的稳定性和背景噪声的干扰，使得信号的峰峰值出现明显的上下波动。同理，图 5b中给出了signal_2和signal_3之间的依赖关系(如“·”所示)，及相应LSM和RANSAC算法线性拟合结果(如“-”所示)，拟合结果相关的参量统计归纳在表 2中。

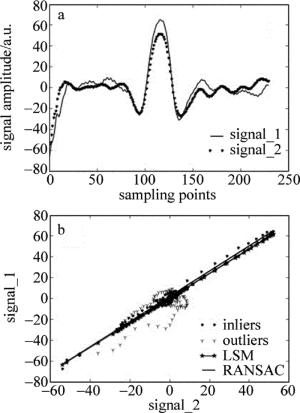
Figure 4.  a—the experimentally measured second harmonic signal of formaldehyde with different concentrations b—the fitting results by using LSM and RANSAC algorithms, respectively

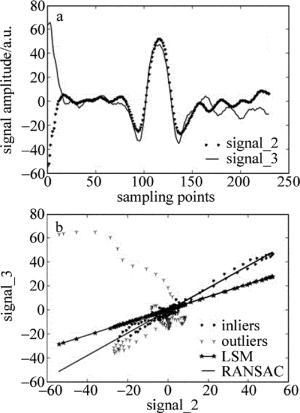
Figure 5.  a—the experimentally measured second harmonic signal of formaldehyde with same concentration b—the corresponding fitted results by using LSM and RANSAC algorithm, respectively

从拟合结果可以看出，LSM在信噪比较低情况下，极易受异常数据的影响，使拟合模型明显偏离，线性相关度较低，拟合的体积分数误差高达47%。而RANSAC算法通过设置阈值来区分内外点，可以很好地排除仪器系统噪声(光学干涉噪声和电子学噪声)的影响，使得拟合线性相关度提高，反演的气体体积分数误差较小。

通过以上对仿真信号和实验数据的分析处理可见，当光谱数据信噪比较高的时候，两种模型拟合结果保持很好的一致性，当光谱数据信噪比较差的时候，尤其是光谱信号受到采集系统噪声的严重干扰，RANSAC算法比LSM更能鲁棒性地估计模型参量，提高线性相关度，减小气体浓度反演的误差。

通过理论和实验研究了RANSAC算法在波长调制吸收光谱数据处理中的应用。结果表明，与传统的LSM相比，RANSAC算法可以很好地适应光谱数据中各种异常情况，对带有误差和异常值的数据集进行拟合并得到线性相关度较高的拟合结果。尤其是在吸收光谱信号较弱(气体浓度较低)、背景噪声影响显著的情况下，RANSAC算法作为一种鲁棒性的线性拟合算法，可很好地排除异常数据的干扰，有效且可靠地反演出样品浓度信息，体现出其在激光光谱高精度测量大气温室气体及其它大气痕量气体应用研究方面的潜力。