-
高光谱图像通过光谱仪采集,能同时获得光谱信息和图像信息,具有图谱合一的优点[1],使得其在军事目标检测、农作物分类、矿物探测等多个领域都得到广泛应用。高光谱图像的光谱分辨率在不断提高,但是空间分辨率仍旧较低。由于高光谱遥感图像在采集图像时,是以像元为单位来获取地面物体的光谱信息,高光谱图像中的每一个像元都对应着具有一定面积的地表区域,而区域的大小由光谱仪的空间分辨率决定。因此,当空间分辨率较低时,图像中将会出现大量混合像元,导致目标的分类精度降低。若一个像元里仅仅包含一种物体,则该像元是纯净像元,包含纯净的光谱信号的像元称之为端元; 当光谱仪空间分辨率较低时,一个像元里含有多种物质混合,则包含混合光谱信号的像元称作混合像元[2]。高光谱像元解混主要分为线性和非线性解混,线性光谱解混相对简单易行,非线性解混考虑了物体的二次散射效应,更符合实际光谱采集情况,但情况相对复杂,相关因素众多,导致解混难度大,仍处于研究初期[3-4]。本文中主要介绍线性光谱解混,经过线性光谱解混, 得到混合像元中各个端元在每个像元中所占的比例,该比例称为丰度,该过程称为丰度反演。
高光谱线性解混主要包括基于几何学和基于统计学光谱解混的两类方法[2],基于几何学方法, 计算简单、计算量小,先提取端元,然后求解丰度;而基于统计学方法,通过迭代求解端元和丰度,计算量较大。
基于几何学光谱解混的典型方法有:像元纯净指数(pixel purity index, PPI)[5]、N-FINDR[6]、顶点成分分析(vertex component analysis, VCA)[7]、自动目标生成(automatic target generation process, ATGP)[8]、正交子空间投影(orthogonal subspace projection, OSP)[9]和连续最大角凸锥(sequential maximum angle convex cone, SMACC)[10]算法等。
基于统计学光谱解混的方法是一种混合信号分离的方法,即把一个矩阵分解成两个矩阵的乘积,主要有:非负矩阵分解(nonnegative matrix factorization, NMF)[11]、独立成分分析(independent component analysis, ICA)[12]和迭代误差分析(iterative error analysis, IEA)[13]等。
近年来,国内外众多学者对混合像元分解方法进行了深入的研究,同时对现有的方法进行了改进和优化,还有结合图像的空间信息进行端元提取。2002年, PLAZA提出了采用自动形态学端元提取(automatic morphological endmember extraction, AMEE)[14]的方法,充分利用了高光谱图像的空间信息和光谱信息,提高了解混精度。
-
假设高光谱数据表达为X={x1, x2, …, xN},其包含N个像元、L个波段,其中xi={y1, y2, …, yL}, xi表示第i个像元的光谱矢量, yL为第L个波段的光谱值,i=1, 2, …, N,根据线性解混模型,高光谱数据又可以表示为P个端元的光谱矩阵及对应的丰度矩阵的组合[2]:
$ \mathit{\boldsymbol{X}} = f\left( {\mathit{\boldsymbol{E}},\mathit{\boldsymbol{S}}} \right) + \mathit{\boldsymbol{n}} $
(1) $ \sum\limits_{z = 1}^P {{s_z}} = 1,\left( {0 \le {s_z} \le 1} \right) $
(2) 式中, f(E, S)表示端元矩阵和丰度矩阵的函数关系式,E=(e1, e2, …, eP)∈RL×P代表包含P个端元的光谱矩阵,eP为第P个端元的光谱;S=(s1, s2, …, sP)T∈RP×N是像元对应的丰度矩阵,sz代表第z个端元的丰度值;n为实际存在的误差及噪声项; (2)式即为丰度约束条件。
-
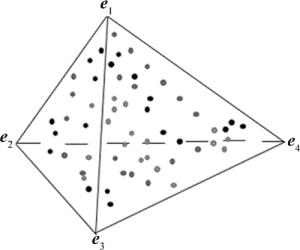
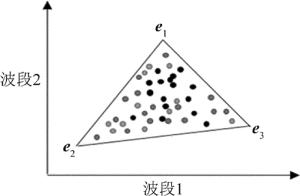
基于几何学的解混方法有一个前提:图像数据中各物质都存在纯净像元(即端元)。几何学方法是根据像元在几何空间的分布特性来提取端元,然后再对图像进行解混。理想情况下认为高光谱数据集的所有像元的空间分布恰好位于一个凸面单形体中[15]。单形体包含所有的数据点,数据点构成的单形体空间中,单形体的顶点就是端元。因此,端元提取是通过寻找对应单形体的顶点来获得端元[16]。在2维空间数据中,单形体看作一个三角形,3维空间数据中单形体是一个棱锥,分别如图 1和图 2所示。在多维空间中单形体是个多面体。
高光谱像元线性解混通常分为端元提取和丰度反演两个部分。基于几何学的端元提取方法中常规方法有PPI, VCA, N-FINDR方法等。
-
像元纯净指数PPI[5]是采用投影的方法来寻找端元。首先,使用最小噪声分离(minimum noise fraction, MNF)[17]降维,然后将所有像元向穿过单形体空间中的随机方向投影,将被投影到两端的点作为潜在的端元。统计每个像元在所有投影方向作为端元点的总次数,次数越多,说明属于端元的概率越大。通过迭代投影的方法找到集合中相对纯净的像元,设定阈值,提取端元。
PPI算法思想简单易行、计算量较小,但是也存在着较多的缺点。PPI的方法属于半监督式方法,端元提取过程中需要人为进行选择,缺乏自动性。同时,由于高光谱维数高,需要先用MNF对数据进行降维,即将高维高光谱数据降为低维数据。有多个投影方向,导致测试耗时量大。同时投影方向随机导致每次提取的结果有差异,算法的鲁棒性差。对此,ZENG[18]引入Givens旋转矩阵选择了0°, 45°, 90°, 135°这4个基本方向作为投影方向, 大幅减少原算法中的投影方向,而且选取的方向又涵盖了各个基本方向,改进了PPI算法,减少了计算,使得算法鲁棒性更好。
-
顶点成分分析(VCA)[7]改进了投影方式。首先计算高光谱图像中的端元数目,假定待提取的端元数目为P, 通过P次迭代计算就可以找到单形体的顶点,即提取出端元。首先,找出图像数据中具有最大投影长度的像元,即模值最大的像元点,作为第1个端元。然后找到一个与该端元光谱方向正交的空间向量,作为第2次迭代的投影方向,将数据集往该方向上投影,找出投影中最大投影值对应的像元,将此像元作为第2个端元。然后将这两个端元组成端元集确定下次的投影方向,找到下一个端元,以此类推,计算出P个端元。
VCA算法计算简单、计算量小,并且结果稳定,提取结果常常被作为其他算法的初始化端元。
-
不同于PPI和VCA算法,N-FINDR算法是通过计算、比较单形体的体积大小,找到构成最大体积对应的像元,作为端元,端元集构成最大单形体体积[6]。首先,对高光谱数据用MNF进行降维,数据维度降成P-1,然后随机选择P个初始的端元点作为端元集。计算由端元集组成的单形体体积。体积计算公式为:
$ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} 1&1& \cdots &1\\ {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2}}& \cdots &{{\mathit{\boldsymbol{e}}_P}} \end{array}} \right] $
(3) $ V\left( \mathit{\boldsymbol{E}} \right) = \frac{{{\rm{abs}}\left( {\left| \mathit{\boldsymbol{E}} \right|} \right)}}{{\left( {P - 1} \right)!}} $
(4) 式中, eP代表端元向量,E为端元集构成的矩阵,V为矩阵的体积,|E|为E的行列式,abs为取绝对值。依次更换一个像元,重新计算体积,反复进行迭代、比较,遍历所有像元点,直至找到构成最大体积的端元集。
N-FINDR算法计算量较大,实际使用时往往设置迭代次数。因此初始端元的选择影响着最后的端元提取结果。
对于N-FINDR算法的改进有很多方法。GENG等人[19]提出一种新的体积计算公式,通过改进体积计算方法,使计算摆脱维数限制。假设单形体的P个顶点为e1, e2, …, eP; AP-1=[e2-e1, e3-e1, …, eP-e1],对行列式进行变换。则单形体体积计算公式为:
$ \begin{array}{*{20}{c}} {\left| {\begin{array}{*{20}{c}} 1&1& \cdots &1\\ {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2}}& \cdots &{{\mathit{\boldsymbol{e}}_P}} \end{array}} \right| = }\\ {\left| {\begin{array}{*{20}{c}} 1&0& \cdots &0\\ {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2} - {\mathit{\boldsymbol{e}}_1}}& \cdots &{{\mathit{\boldsymbol{e}}_P} - {\mathit{\boldsymbol{e}}_1}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} 1&0\\ {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{A}}_{P - 1}}} \end{array}} \right|} \end{array} $
(5) $ \begin{array}{*{20}{c}} {\det \left[ {\begin{array}{*{20}{c}} 1&1& \cdots &1\\ {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2}}& \cdots &{{\mathit{\boldsymbol{e}}_P}} \end{array}} \right] = \det \left[ {\begin{array}{*{20}{c}} 1&0\\ {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{A}}_{P - 1}}} \end{array}} \right] = }\\ {\det \left( {{\mathit{\boldsymbol{A}}_{P - 1}}} \right) = {{\left| {\det \left( {{{\left( {{\mathit{\boldsymbol{A}}_{P - 1}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{A}}_{P - 1}}} \right)} \right|}^{\frac{1}{2}}}} \end{array} $
(6) 式中,det表示行列式的值,T表示转置。由于(AP-1)TAP-1是方阵,所以此公式能应用于任何维度的高光谱数据,则采用N-FINDR算法时不需要先进行降维处理。
采用上述几何学方法提取端元之后,再通过丰度反演求解出各个端元对应的丰度。目前已经有大量算法来进行丰度反演。如最小二乘法、凸面几何学分析方法、独立成分分析法、滤波向量法、投影寻踪法、端元投影向量法、正交子空间投影法等[20]。其中线性光谱解混中应用最广泛的方法是基于最小二乘法的反演算法。
-
依据丰度非负以及和为一这两个约束条件,可以将最小二乘法分为无约束最小二乘法(unconstrained least squares, UCLS)、非负约束最小二乘法(nonnegative constrained least squares, NCLS)、和为一约束最小二乘法((sum-to-one constrained least squares, SCLS)、全约束最小二乘法(fully constrained least squares, FCLS)[21]4种。
在不考虑任何约束时,用无约束最小二乘法(UCLS)求解(1)式,丰度可以表示为:
$ {\mathit{\boldsymbol{S}}_{{\rm{UCLS}}}} = {\left( {{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{E}}} \right)^{ - 1}}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{X}} $
(7) 当加入非负约束(NCLS)时,由于存在不等式约束,模型没有解析解,利用迭代方法获得最优解,迭代求解公式为:
$ {{\mathit{\boldsymbol{\hat S}}}_{{\rm{NCLS}}}} = {\left( {{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{E}}} \right)^{ - 1}}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{X}} - {\left( {{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{E}}} \right)^{ - 1}}\lambda $
(8) 式中,λ为拉格朗日乘子:
$ \lambda = {\mathit{\boldsymbol{E}}^{\rm{T}}}\left( {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{E}}{{\mathit{\boldsymbol{\hat S}}}_{{\rm{NCLS}}}}} \right) $
(9) 当仅加入和为一约束(SCLS)时,利用拉格朗日乘子法求解,可得丰度向量为:
$ \begin{array}{*{20}{c}} {F\left( \mathit{\boldsymbol{S}} \right) = \frac{1}{2}{{\left( {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{ES}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{ES}}} \right) + }\\ {\lambda \left( {{\bf{1}} - {{\bf{1}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)} \end{array} $
(10) $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat S}}}_{{\rm{SCLS}}}} = {{\left( {{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{E}}} \right)}^{ - 1}}{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{X + }}}\\ {{{\left( {{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{E}}} \right)}^{ - 1}}{\bf{1}}\left( {{{\bf{1}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{E}}} \right)}^{ - 1}}{\bf{1}}} \right)\left( {{\bf{1}} - {{\bf{1}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)} \end{array} $
(11) 式中, F(S)为拉格朗日函数,1为含有P个1的列向量。
FCLS考虑了所有约束条件,更符合实际情况,本文中采用FCLS进行丰度反演。HEINZ等人[21]对高光谱数据矩阵X和端元矩阵E引入影响因子δ,对两个矩阵做了变形求解:
$ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{E}}}\\ {{{\bf{1}}^{\rm{T}}}} \end{array}} \right],\mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{X}}}\\ {\bf{1}} \end{array}} \right] $
(12) 利用这种变形,FCLS的解可以根据UCLS算法求得。
-
像元x可以看作信号光谱T和背景光谱B两部分组成,表示为:
$ {\mathit{\boldsymbol{x}}_i} = \mathit{\boldsymbol{T}} + \mathit{\boldsymbol{B}} + \mathit{\boldsymbol{n}} $
(13) 式中,n为噪声。将端元矩阵分为信号光谱和背景光谱两部分,用背景光谱的正交子空间设计滤波器,使混合像元进行滤波处理,去除背景光谱,剩下信号光谱,求解信号端元的丰度。依次更改端元矩阵中的信号光谱与背景光谱,得到混合像元中每个端元对应的丰度值[22]。
综上所述,几何学方法基于几何理论,首先提取端元,然后再进行丰度反演。但是统计学方法能够同时得到端元和丰度矩阵。
-
高光谱线性解混方法中基于统计学的方法,主要包括非负矩阵分解、独立成分分析和迭代误差分析等。
-
非负矩阵分解(NMF)是将一个矩阵分解成两个非负矩阵乘积的过程。解混时使得端元矩阵和丰度矩阵的重构的图像数据,相对原图像数据误差最小化。LEE等人提出用欧氏距离来表示这一过程,常采用欧氏距离的平方[23]:
$ f\left( {\mathit{\boldsymbol{E}},\mathit{\boldsymbol{S}}} \right) = \frac{1}{2}\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{ES}}} \right\|_F^2 $
(14) $ \left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{ES}}} \right\|_F^2 = \sum\limits_{ij} {{{\left( {{\mathit{\boldsymbol{X}}_{ij}} - {{\left( {\mathit{\boldsymbol{ES}}} \right)}_{ij}}} \right)}^2}} $
(15) 式中, ‖·‖F代表F范数。NMF采用梯度更新迭代公式。通常计算量较大,一般设置最大迭代次数和最大误差得到端元矩阵和丰度矩阵。在实际应用中难以得到全局最优,经常陷入局部最优。为此通过引入约束条件来缓解局部最优的问题,例如,MIAO等人[24]通过把最小体积约束附加到NMF中,使得最终的端元集尽可能准确。另外还有把平滑性和稀疏性, 以及以最小距离作为约束条件,都得到了更好的结果[25-26]。
在NMF的初始端元设置时,可以将基于几何学方法提取的端元作为初始端元,通过改进初始端元的选取,避免最终结果为局部最优解,同时可以减少迭代计算时间。
-
独立成分分析(ICA)属于一种非监督盲源信号分离的方法。通常假设信号源是独立,且数据是非高斯分布[12]。高光谱数据作为混合信号,将端元光谱或者丰度作为源信号,应用ICA进行盲解混。BAYLISS等人[27]以端元光谱作为源信号,使用ICA进行解混。后来经过其他学者的研究发现,以丰度作为信号源解混效果更好,具有更多的统计信息[28-29]。
ICA方法对数据所做的非高斯分布独立性假设与实际情况不相吻合,真实数据大体上符合高斯分布,这是ICA解混方法的主要问题。
基于统计学的方法能够同时提取出端元矩阵和丰度矩阵,但是求解过程相对复杂,计算量大。
-
迭代误差分析(IEA)不需要对数据进行降维,通过计算误差的大小判断端元位置。首先将数据均值作为初始向量,然后由最小二乘法解混,求解一个估计丰度,根据已有端元和丰度重构图像,找到误差最大的像元作为新的端元;再由更新的端元集迭代,再次解混,直至找到P个端元或误差达到设定值。
IEA通过不断更新端元集,对每一个像元迭代求解,能同时求解端元和丰度,解混精度相对较高,但是每次都要计算各像元的模值,总体计算量较大。对此,ZHAO等人提出一种改进的迭代误差分析方法[13],求端元集的正交子空间,把所有像元投影到该子空间中,去掉投影值小于阈值的像元,计算剩余像元的均方根误差。通过投影的方法减少了冗余像元的计算。
-
高光谱不仅含有光谱信息,同时还包含普通图像的空间信息。2002年, PLAZA将数学形态学方法应用于多光谱图像像元解混中,实现了多光谱图像结合空间信息的端元自动提取(automatic morphological endmember extraction, AMEE)[14], 融合空间信息提高了解混精度。同时,使得AMEE运用于高光谱端元提取成为现实。
AMEE算法采用数学形态学中膨胀和腐蚀两种运算方法,将空间和光谱信息结合再对高光谱数据进行端元提取, 该方法不需要提前进行降维。首先, 设置最小和最大空间窗,称为结构元素。图像数据在结构元素内进行膨胀和腐蚀基本操作,依次在每个邻域空间中得到最纯光谱像元和混合度最高的像元,用形态学离心指数(morphological eccentricity index, MEI)判断结构元素内像元纯度,其中MEI值由光谱角余弦值计算。依次增大结构元素大小直至预设的最大值,求取所有的MEI值的平均值作为阈值,若像元的MEI值大于该阈值,则该像元属于端元[14]。此后,又有学者提出了一些空间预处理的方法[30-32],结合空间信息, 得到了比较好的解混效果。
高光谱线性解混方法及其改进优化方法有很多,各种方法也各有特点。目前这些方法中,主要存在的问题是对图像中异常点的处理,异常点对端元提取的影响十分严重,主要的解决思路是根据物体的聚类特性,结合空间信息消除异常点。
-
本文中用1997年AVIRIS获取的美国内达华州Cuprite矿物区真实高光谱数据进行端元提取,然后利用FCLS解混,比较端元矩阵和丰度矩阵的重构图像与原数据的均方根误差(root mean square error, RMSE)[16]大小,综合判断端元提取方法的特点。对Cuprite数据裁剪得到大小为100×100的高光谱数据,图 3中为第40、第21、第11波段合成的RGB图像,数据波长范围为0.37μm~2.51μm,低信噪比波段第98~第128, 第148~第170被移除,本实验中总共采用170个波段。
实验中采用PPI, N-FINDR, ATGP, SMACC和IEA这5种端元提取方法和FCLS进行丰度反演。5种端元提取及丰度反演之后的RMSE分别如图 3b~图 3f所示,图 3g为RMSE的图例。均方根误差图像中,每个像元的误差值由图例所示颜色来表示,数值越大,代表算法的误差越大。从图中可以看出,在本实验中,IEA和N-FINDR算法的解混精度相对其它算法的解混精度更高,这两种算法对噪声的抑制效果更佳。表 1为5种方法的RMSE数值。通过各个算法总体的RMSE数值也可以看出,IEA和N-FINDR算法的均方根误差相对更小,而ATGP和SMACC这两种算法精度最低,因为其通过寻找最亮的像元点,及与该像元点差别最大的点,算法受误差及噪声影响较大。根据实验结果及过程将各方法的特点进行了归纳对比,如表 2所示。
表 1 端元提取算法的均方根误差
方法 PPI N-FINDR ATGP SMACC IEA 均方根误差 231.6982 138.7092 398.2158 335.0004 106.1878 表 2 常用端元提取算法的特点
方法 全自动 降维 使用空间信息 算法复杂性 解混精度 PPI 否 是 否 容易 较高 N-FINDR 是 是/否 否 容易 高 ATGP 是 否 否 容易 较低 SMACC 是 否 否 容易 较低 NMF 是 否 否 复杂 较高 IEA 是 否 否 复杂 高 AMEE 是 否 是 容易 高 从这几种典型的端元提取方法可以看出,基于几何学的解混方法复杂度较低,基于统计学盲源信号分离的方法复杂度较高,但解混精度相对更高。大部分算法属于全自动,只有PPI算法需要手动划分感兴趣区,属于半自动。同时可以看到,大部分算法中考虑空间信息的算法相对较少。
-
对高光谱解混方法中的线性解混方法进行了简要的介绍与总结。总体而言,高光谱线性解混方法是目前研究的重点内容。基于几何学理论的解混方法相对较多,其思路简单易行。基于统计学的方法,算法复杂度相对更高。
笔者认为今后应该主要从以下几个方面对高光谱解混作进一步研究:
(1) 将高光谱图像中的空间信息与光谱信息相结合。高光谱图像不仅仅包含光谱信息,而且还具有普通图像的空间位置信息。将空间信息与光谱信息进行融合,能够减少图像中异常点的影响。使用张量表达的方法融合高光谱图像的多种特性,提高解混精度。
(2) 充分结合高光谱图像数据自身独特的特点,结合稀疏性和空间中相同物质的聚类特性来进行解混。
(3) 借鉴线性解混方法,依据非线性解混方法的特点,研究采用更符合实际情况的非线性解混方法来解混。非线性解混方法考虑了二次散射,更加符合实际物体间光谱的作用情况。
(4) 改善和优化非线性解混算法的核函数形式,简化计算。非线性解混算法相对复杂,现有的非线性解混大部分利用高斯径向基核函数。考虑如何针对高光谱数据特性,改进核函数,改善其性能,提高解混效率。
随着高光谱遥感技术的发展,图像中包含的信息将会更加丰富,数据量更大,高光谱解混将会更加重要,在单个像元以及其子像元方面的研究会更加深入。
高光谱解混方法研究
Research of hyperspectral unmixing methods
-
摘要: 高光谱图像的空间分辨率较低,导致大量混合像元存在于高光谱图像中。混合像元的存在是使高光谱图像目标分类准确率降低的主要原因之一。高光谱像元解混在高光谱遥感图像处理中具有非常重要的意义。高光谱像元解混主要分为线性和非线性光谱解混两种方法,研究最广泛的是线性光谱解混。归纳了线性光谱解混的两个步骤:(1)提取纯净像元中地物的光谱信号,即提取端元,这是关键步骤;(2)利用端元的加权线性组合对混合像元进行光谱解混,即丰度反演。简述了端元提取及丰度反演研究的主要进展,介绍了端元提取的几种典型算法。通过归纳、对比和分析,总结了不同端元提取方法的特点,并对高光谱解混的研究前景进行了展望。Abstract: Because spatial resolution of hyper-spectral images is low, a large number of the mixed pixels were in hyper-spectral images. The presence of the mixed pixels is one of the main reasons of the low accuracy of target classification in hyper-spectral images. Hyper spectral pixel unmixing is of great importance in hyper-spectral remote sensing image processing. Hyper-spectral unmixing is divided into two methods:linear and nonlinear spectral unmixing. Linear spectral unmixing has been studied most widely. Two steps of linear spectral mixing are summed up:firstly, spectral signals of ground objects in the pure pixels are extracted, that is, end-members are extracted. It is the key step. The weighted linear combination of end-members is used to unmix the spectral image of the mixed pixels, that is, the abundance inversion. Main progress of end-member extraction and abundances inversion is briefly introduced, and several typical algorithms for end-member extraction are introduced. Through summing-up, contrasting and analyzing, the characteristics of different endmember extraction methods are summarized. The prospect of hyperspectral unmixing is prospected.
-
Key words:
- spectroscopy /
- hyperspectral image /
- linear unmixing /
- endmember extraction
-
表 1 端元提取算法的均方根误差
方法 PPI N-FINDR ATGP SMACC IEA 均方根误差 231.6982 138.7092 398.2158 335.0004 106.1878 表 2 常用端元提取算法的特点
方法 全自动 降维 使用空间信息 算法复杂性 解混精度 PPI 否 是 否 容易 较高 N-FINDR 是 是/否 否 容易 高 ATGP 是 否 否 容易 较低 SMACC 是 否 否 容易 较低 NMF 是 否 否 复杂 较高 IEA 是 否 否 复杂 高 AMEE 是 否 是 容易 高 -
[1] ZHANG L P, ZHANG L F. Hyperspectral remote sensing[M].Wuhan:Wuhan University Press, 2005:26-27(in Chinese). [2] XIA W. Researches on the methods of unmixing and band selection for hyperspectral remote sensing images[D]. Shanghai: Fudan University, 2013: 15-16(in Chinese). [3] NASH D B, CONEL J E. Spectral reflectance systematics for mixtures of powdered hypersthene, labradorite, and ilmenite[J].Journal of Geophysical Research, 1974, 79(11):1615-1621. doi: 10.1029/JB079i011p01615 [4] BRUCE H. Book review:Theory of reflectance and emittance spectroscopy[M].Cambridge:Cambridge University Press, 1993:455-460. [5] BOARDMAN J W, KRUSE F A, GREEN R O.Mapping target signatures via partial unmixing of AVIRIS data in summaries[C]//Summaries, Fifth JPL Airborne Earth Science Workshop. Pasadena, USA: JPL Publication, 1995: 23-262. [6] WINTER M E. N-FINDR:an algorithm for fast autonomous spectral endmember determination in hyperspectral data[J].Proceedings of the SPIE, 1999, 3753:266-275. doi: 10.1117/12.366289 [7] NASCIMENTO J M P, DIAS J M B.Vertex component analysis:a fast algorithm to unmix hyperspectral data[J].IEEE Transactions on Geosciences and Remote Sensing, 2005, 43(4):898-910. doi: 10.1109/TGRS.2005.844293 [8] ZHUO L, CAO J J, WANG F, et al. Blind unmixing based on improved target endmember for hyperspectral imagery[J]. Journal of Remote Sensing, 2015, 19(2):273-287(in Chinese). [9] HARSANYI J C, CHANG C I. Hyperspectral image classification and dimensionality reduction:an orthogonal subspace projection approach[J].IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4):779-785. doi: 10.1109/36.298007 [10] GRUNINGER J, RATKOWSKI A J, HOKE M L. The sequential maximum angle convex cone endmember model[J].Proceedings of the SPIE, 2004, 5425:1-14. doi: 10.1117/12.543794 [11] JIA S, QIAN Y T. Constrained nonnegative matrix factorization for hyperspectral unmixing[J].IEEE Transaction on Geoscience and Remote Sensing, 2009, 47(1):161-173. doi: 10.1109/TGRS.2008.2002882 [12] HYVARINEN A, KARHUNEN J, OJA E. Independent component analysis[M].New York, USA:John Wiley & Sons Ltd, 2001:89-96. [13] ZHAO Ch H, CUI Sh L, ZHAO G P, et al. Endmember extraction algorithm based on improved iterative error analysis[J]. Journal of Harbin Engineering University, 2015, 36(2):257-261(in Chinese). [14] PLAZA A, MARTINEZ P, PEREZ R, et al. Spatial/spectral endmember extraction by multidimensional morphological operations[J].IEEE Transactions on Geosciences and Remote Sensing, 2002, 40(9):2025-2040. doi: 10.1109/TGRS.2002.802494 [15] SHEN W X. Simplex theory guidance:high dimensional generalization of triangles[M].Changsha:Hunan Normal University Press, 2000:35(in Chinese). [16] ANTONIO P, PABLO M, ROSA P, et al. A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data[J].IEEE Transaction on Geoscience and Remote Sensing, 2004, 42(3):650-663. doi: 10.1109/TGRS.2003.820314 [17] WANG K, QU H M. Anomaly detection method based on improved minimum noise fraction transformation[J].Laser Technology, 2015, 39(3):381-385(in Chinese). [18] ZENG F X. The improvement and optimization of endmembers extraction in hyperspectral remote sensing image[D].Chengdu: Chengdu University of Technology, 2013: 19-20(in Chinese). [19] GENG X, ZHAO Y, WANG F, et al. A new volume formula for a simplex and its application to endmember extraction for hyperspectral image analysis[J].International Journal of Remote Sensing, 2010, 31(4):1027-1035. doi: 10.1080/01431160903154283 [20] CHARLES L, LAWSON, RICHARD J. Solving least squares pro-blem[M].New Jersey, USA:Prentice-Hall, 1995:64-80. [21] HEINZ D C, CHANG C I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery[J].IEEE Transaction on Geoscience and Remote Sensing, 2001, 39(3):529-545. doi: 10.1109/36.911111 [22] MEI Sh H, HE M Y. A novel spectrum filter for fully constrained mixture analysis[J]. Journal of Remote Sensing, 2010, 14(1):68-79. [23] LEE D D, SEUNG H S. Learning the parts of objects by nonnegative matrix factorization[J].Nature, 1999, 401(6755):788-791. doi: 10.1038/44565 [24] MIAO L, QI H. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix fraction[J].IEEE Transaction on Geoscience and Remote Sensing, 2007, 45(3):765-777. doi: 10.1109/TGRS.2006.888466 [25] QIAN Y T, JIA S. Hyperspectral unmixing via L1/2 sparsity-constrained nonnegative matrix factorization[J].IEEE Transaction on Geoscience and Remote Sensing, 2011, 49(11):4282-4297. doi: 10.1109/TGRS.2011.2144605 [26] YU Y, GUO Sh, SUN W D. Minimum distance constrained nonnegative matrix factorization for the end-member extraction of hyperspectral images[J]. High Technology Letters, 2012, 18(4):333-342. [27] BAYLISS J D, GUALTIERI J A, CROMP R F. Analyzing hyperspectral data with independent component analysis[J].Proceedings of the SPIE, 1998, 3240:133-143. doi: 10.1117/12.300050 [28] CHEN C H, ZHANG X. Independent component analysis for remote sensing study[J].Proceedings of the SPIE, 1999, 3871:150-158. doi: 10.1117/12.373252 [29] CHIANG S S, CHANG C I, GINSBERG I W. Unsupervised hyperspectral image analysis using independent component analysis[C]//Proceedings, Geoscience and Remote Sensing Symposium. Honolulu, HI, USA: IEEE International Geoscience & Remote Sensing, 2000: 3136-3138. [30] ZORTEA M, PLAZA A. Spatial preprocessing for endmember extraction[J]. IEEE Transaction on Geoscience and Remote Sensing, 2009, 47(8):2679-2693. doi: 10.1109/TGRS.2009.2014945 [31] MARTIN G, PLAZA A. Region-based spatial preprocessing for endmember extraction and spectral unmixing[J].IEEE Transaction on Geoscience and Remote Sensing, 2011, 8(4):745-749. doi: 10.1109/LGRS.2011.2107877 [32] MARTIN G, PLAZA A. Spatial-spectral preprocessing prior to endmember identification and unmixing of remotely sensed hyperspectral data[J].IEEE Transaction on Geoscience and Remote Sensing, 2012, 5(2):380-395. -


 网站地图
网站地图

 下载:
下载: