网站地图
下载:
-
无线传感器网络[1](wireless sensor networks, WSN)是近年来国内外高度重视的一种信息技术之一，在水产养殖业、物联网、仓储系统、军事安全以及防火防盗等领域有着广泛应用。在大多数应用中，在节点位置已知的情况下采集到的数据才有意义。常见的全球定位系统(global positioning system, GPS)虽然精度高，但面对规模庞大的无线传感器网络，使用GPS定位将导致整个系统成本高、功耗大，并制约了系统扩展性。当然也有利用传感器[2]和其它算法[3]的定位方式，但考虑到成本以及功耗问题，本文中主要研究无线传感器网络定位算法。现阶段，定位算法主要分为基于测距[4]和无需测距[5]。基于测距的主要有接收信号强度指示(received signal strength indicator, RSSI)[6]、到达时间差(time difference of arrival, TDOA)[7]、到达时间(time of arrival, TOA)[8]以及到达角(angle of arrival, AOA)[9]等定位算法，这些算法定位精度高，但对硬件要求高、成本高、计算度复杂，增加了系统的功耗。无需测距技术的定位算法主要有质心[10]、DV-Hop(distance vector-hop)[11-14]、Amorphous[15]、凸规划[16]以及近似三角形内点测试法(approximate point-in-triangulation test, APIT)定位算法，其中APIT定位算法功耗低、成本低、定位性能好，且不依赖于硬件设施，因此被广泛应用。但由于信标节点覆盖率低、节点分布不均匀，在最佳三角形内点测试法(perfect point-in-triangulation test, PIT)测试时容易出现in-to-out和out-to-in误判，导致定位精度难以提高。针对以上问题，本文中提出一种基于向量积同向技术的改进APIT定位算法，该定位算法在PIT测试时无需通过与邻居节点交换信息来模拟节点移动，而是通过利用RSSI定位算法对未知节点进行初步定位，然后利用数学中向量积方向作为判据来替代PIT测试法，从而提高节点的定位精度。
-
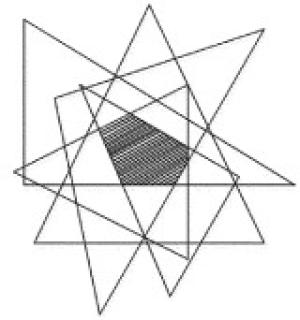
APIT定位算法是由弗吉尼亚大学HE等人提出的一种定位算法。如图 1所示，在该定位算法中，未知节点收集所有能与之通信的信标节点，然后从这些信标节点中任取3个组成信标三角形，假设与未知节点通信的信标节点共有n个，那么就有Cn3个信标三角形，并筛选出包含未知节点的信标三角形，将这些信标三角形重叠区域求质心，即为未知节点的位置。
Figure 1. Positioning principle of APIT
-
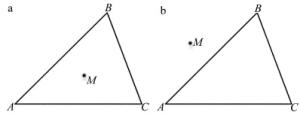
APIT定位算法的理论基础是PIT测试法，通过PIT测试法筛选出包含未知节点的信标三角形，如图 2所示。M为未知节点，A, B, C为信标节点，假设M沿某方向移动时，同时远离或靠近A, B, C这3个点，则点M在△ABC外面，相反点M在△ABC内部。
Figure 2. Principle of PIT
由于在静态网络中节点是固定的，因此通过未知节点与其邻节点间的信息交换来模拟未知节点移动。假设未知节点M接收到信标节点A, B, C的RSSI值分别为RA, RB, RC，那么未知节点M移动至某一邻居节点时，收到A, B, C的RSSI值就是该邻居节点在此处收到A, B, C的RSSI值，分别为RA′, RB′, RC′，当存在某一邻居节点使得下面(1)式或(2)式成立时，则点M在△ABC外面，相反点M在△ABC内部。
$ \left\{ \begin{array}{l} {R_A} > {{R'}_A}\\ {R_B} > {{R'}_B}\\ {R_C} > {{R'}_C} \end{array} \right. $
(1) $ \left\{ \begin{array}{l} {R_A} < {{R'}_A}\\ {R_B} < {{R'}_B}\\ {R_C} < {{R'}_C} \end{array} \right. $
(2) -
在节点分布稀疏或不均匀时PIT测试法很容易产生误判。如图 3a所示，当未知节点M与邻居节点3交换信息时，判断M在三角形外面，产生内判外(in-to-out)的误判；如图 3b所示，当未知节点M与邻居节点3或4交换信息时，判断M在三角形里面，产生外判内(out-to-in)的误判。而in-to-out和out-to-in是造成APIT定位误差的主要因素，因此，对APIT定位算法进行改进的关键是解决PIT测试法的误判问题。
Figure 3. Misjudgment situation
-
(1) 信标节点以广播的方式发送自身信息(坐标、信号强度等)，然后未知节点收集所有能与之通信的节点的信息；(2)未知节点与邻节点之间交换信息，筛选出包含未知节点的信标三角形；(3)求出筛选出的信标三角形重叠区域，计算出其质心位置作为未知节点的位置；(4)完成定位。
-
针对in-to-out和out-to-in误判问题，本文中提出一种利用向量积方向是否相同来判断未知节点是否在信标三角形内部的改进APIT定位算法。
定义1：如图 4所示，A, B, C为信标三角形的3个顶点，M为未知节点，当同时满足以下3个条件时，未知节点M在信标三角形ABC内部，否则未知节点M在信标三角形ABC外面:(1)点M和点A在BC的同一侧；(2)点M和点B在AC的同一侧；(3)点M和点C在AB的同一侧。
Figure 4. Unknown node outside and inside the beacon triangle
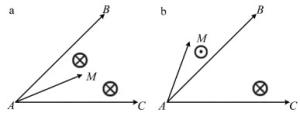
定义2：如图 5所示，⊙表示叉乘结果的方向由内向外，$ \otimes $表示叉乘结果的方向由外向内，A, B, C为平面内3个点，以判断点M和点C在AB的同一侧为例，分别构造$\overrightarrow {AC} , \overrightarrow {AM} , \overrightarrow {AB} $3个向量，然后根据右手定则，如果$\overrightarrow {AB} \times \overrightarrow {AM} $和$\overrightarrow {AB} \times \overrightarrow {AC} $叉乘结果方向一致(符号相同)，则点M和点C在AB的同一侧，否则点M和点C在AB的两侧。
Figure 5. Vector product direction
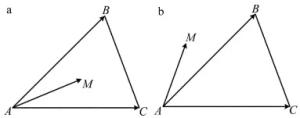
如图 6所示，A, B, C为信标三角形3个顶点，M为未知节点，假设A, B, C, M坐标分别为(xA, yA), (xB, yB), (xC, yC)，(xM, yM)，判断M是否在△ABC内，主要分以下3个步骤。
Figure 6. To determine whether the unknown node is within the beacon triangle or not
-
$ \overrightarrow {AB} = \left( {{x_B} - {x_A}, {y_B} - {y_A}} \right) $
(3) $ \overrightarrow {AM} = \left( {{x_M} - {x_A}, {y_M} - {y_A}} \right) $
(4) $ \overrightarrow {AC} = \left( {{x_C} - {x_A}, {y_C} - {y_A}} \right) $
(5) $ \begin{array}{*{20}{c}} {\overrightarrow {AB} \times \overrightarrow {AM} = \left( {{x_B} - {x_A}} \right)\left( {{y_M} - {y_A}} \right) - }\\ {\left( {{y_B} - {y_A}} \right)\left( {{x_M} - {x_A}} \right)} \end{array} $
(6) $ \begin{array}{*{20}{c}} {\overrightarrow {AB} \times \overrightarrow {AC} = \left( {{x_B} - {x_A}} \right)\left( {{y_C} - {y_A}} \right) - }\\ {\left( {{y_B} - {y_A}} \right)\left( {{x_C} - {x_A}} \right)} \end{array} $
(7) 根据定义2，如果$\overrightarrow {AB} \times \overrightarrow {AM} $和$\overrightarrow {AB} \times \overrightarrow {AC} $的符号相同，即$\overrightarrow {AB} \times \overrightarrow {AM} $和$\overrightarrow {AB} \times \overrightarrow {AC} $叉乘结果方向一致，那么点M和点C则在AB同一侧，否则点M和点C在AB的两侧。
-
$ \overrightarrow {CA} = \left( {{x_A} - {x_C}, {y_A} - {y_C}} \right) $
(8) $ \overrightarrow {CM} = \left( {{x_M} - {x_C}, {y_M} - {y_C}} \right) $
(9) $ \overrightarrow {CB} = \left( {{x_B} - {x_C}, {y_B} - {y_C}} \right) $
(10) $ \begin{array}{*{20}{c}} {\overrightarrow {CA} \times \overrightarrow {CM} = \left( {{x_A} - {x_C}} \right)\left( {{y_M} - {y_C}} \right) - }\\ {\left( {{y_A} - {y_C}} \right)\left( {{x_M} - {x_C}} \right)} \end{array} $
(11) $ \begin{array}{*{20}{c}} {\overrightarrow {CA} \times \overrightarrow {CB} = \left( {{x_A} - {x_C}} \right)\left( {{y_B} - {y_C}} \right) - }\\ {\left( {{y_A} - {y_C}} \right)\left( {{x_B} - {x_C}} \right)} \end{array} $
(12) 根据定义2，如果$\overrightarrow {CA} \times \overrightarrow {CM} $和$\overrightarrow {CA} \times \overrightarrow {CB} $的符号相同，即$\overrightarrow {CA} \times \overrightarrow {CM} $和$\overrightarrow {CA} \times \overrightarrow {CB} $叉乘结果方向一致，那么点M和点B则在AC同一侧，否则点M和点B在AC的两侧。
-
$ \overrightarrow {BC} = \left( {{x_C} - {x_B}, {y_C} - {y_B}} \right) $
(13) $ \overrightarrow {BM} = \left( {{x_M} - {x_B}, {y_M} - {y_B}} \right) $
(14) $ \overrightarrow {BA} = \left( {{x_A} - {x_B}, {y_A} - {y_B}} \right) $
(15) $ \begin{array}{*{20}{c}} {\overrightarrow {BC} \times \overrightarrow {BM} = \left( {{x_C} - {x_B}} \right)\left( {{y_M} - {y_B}} \right) - }\\ {\left( {{y_C} - {y_B}} \right)\left( {{x_M} - {x_B}} \right)} \end{array} $
(16) $ \begin{array}{*{20}{c}} {\overrightarrow {BC} \times \overrightarrow {BA} = \left( {{x_C} - {x_B}} \right)\left( {{y_A} - {y_B}} \right) - }\\ {\left( {{y_C} - {y_B}} \right)\left( {{x_A} - {x_B}} \right)} \end{array} $
(17) 根据定义2，如果$\overrightarrow {BC} \times \overrightarrow {BM} $和$\overrightarrow {BC} \times \overrightarrow {BA} $的符号相同，即$\overrightarrow {BC} \times \overrightarrow {BM} $和$\overrightarrow {BC} \times \overrightarrow {BA} $叉乘结果方向一致，那么点M和点A则在BC同一侧，否则点M和点A在BC的两侧。
根据定义1，如果点M和点A在BC的同一侧；点M和点B在AC的同一侧；点M和点C在AB的同一侧。那么未知节点M则在信标三角形内部，否则未知节点M在信标三角形外面。
如图 6a所示，满足定义1和定义2，故未知节点M在信标三角形内部；如图 6b所示，不满足定义1和定义2，故未知节点M在信标△ABC外面。
本文中提出的改进APIT算法最大优势是避免了未知节点与邻居节点信息交换时产生的in-to-out和out-to-in误判，并且不存在边界点误判的问题。
-
改进的APIT定位算法从RSSI测距和向量积同向法两方面来提高节点的定位精度，详细步骤如下：(1)信标节点以广播的方式发送自身信息(坐标、信号强度等)，未知节点M收集能与之通信的信标节点的信息，假设与未知节点M通信的信标节点个数为n，若n≥3，执行下一步，否则结束定位; (2)未知节点M收集信标节点的坐标信息和RSSI值，利用极大似然估计法求出未知节点的初步定位位置; (3)从n个信标节点中任选3个组成信标三角形Ai(i=1, 2, 3, …, Cn3)，根据初步定位位置、定义1和定义2筛选出包含未知节点M的信标三角形; (4)求出筛选后信标三角形重叠区域，其重叠区域质心即为未知节点M的定位位置; (5)完成未知节点M的定位。
-
为了分析改进APIT定位算法的性能，本文中使用MATLAB 2016b对该算法进行仿真。仿真环境设定在一个1000m×1000m的2维平面内，随机分布300个节点，节点通信半径设置为200m，信标节点所占比例设置为0.2。首先对原APIT定位算法和改进APIT定位算法进行仿真对比，然后通过对不同参量设置不同值将APIT和改进APIT定位算法进行仿真对比。针对各种情况分别进行50次仿真，取这50次仿真的平均值作为最后的仿真结果。
图 7是在节点通信半径为200m、信标节点占总节点比例为0.2的情况下，APIT定位算法与改进APIT定位算法的仿真结果。图中星号为信标节点，圆圈为未知节点，直线为未知节点实际位置和定位位置的距离差。对比图 7b和图 7c可知，基于向量积同向技术的改进APIT算法定位精度高于传统APIT算法的定位精度。
Figure 7. Positioning error of APIT and the improved APIT
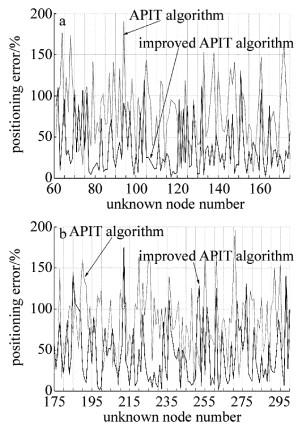
为了便于对比APIT定位算法和改进APIT定位算法的定位误差，这里将两种定位算法定位误差整合到同一折线图中，图 8中，横坐标为未知节点编号，纵坐标为定位的误差。
从图 8a和图 8b中可以更清晰地看出，基于向量积同向技术的改进APIT算法定位精度高于传统APIT算法的定位精度。但仍然存在个别未知节点定位精度差，例如编号为212的节点，造成这种情况的原因是由于改进算法筛选信标三角形时准确度更高，筛选到的信标三角形更多，那么这些信标三角形重叠区域就更大了，质心位置则越偏离真实位置，因此定位精度就越差。但这种情况是极少数的，总体来说改进APIT定位算法的定位精度更高。
Figure 8. Positioning error integration of APIT and the improved APIT
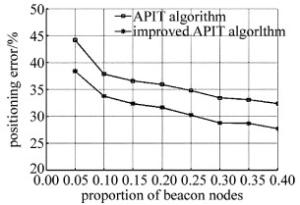
图 9是APIT定位算法和基于向量积同向技术的改进APIT定位算法在信标节点不同比例下的定位误差图。分析图 9可以看出, 随着信标节点比例的增加，定位误差随之减小，且改进APIT定位算法的定位精度更高。通过以上分析，说明改进APIT定位算法的性能优于传统APIT定位算法。
Figure 9. Comparison of positioning error with different proportions of beacon nodes
-
本文中从APIT定位算法内点测试法产生的in-to-out和out-to-in误判作为切入点，提出基于三角形同向技术的改进APIT定位算法，该算法将数学中向量积知识和RSSI技术相结合提出新的内点测试法，仿真实验表明：改进的APIT定位算法比APIT定位算法在信标节点比例不同时定位误差更小、精度更高、算法简单，且不存在边界点误判问题，仿真过程接近实际环境，在现实环境中有很大的实用性。当然，影响定位精度的因素还有节点分布、节点密度以及通信半径等，这将是下一步的研究工作。
基于向量积同向技术的改进APIT定位算法
An improved APIT localization algorithm based on the same side technique of vector product
-
摘要: 近似三角形内点测试（APIT）定位算法在用最佳三角形内点测试法测试时容易产生in-to-out和out-to-in错误，影响定位精度。为了解决这一问题，提出了一种基于向量积同向技术的改进APIT定位算法。采用接收信号强度指示定位算法实现节点的初步定位，然后用向量积同向技术代替内点测试法，提高了定位效率；在MATLAB仿真平台上进行仿真，取得了APIT定位算法和改进APIT定位算法各自产生的定位误差数据。结果表明，在信标节点比例不同的情况下，改进的APIT算法定位精度明显优于APIT算法。Abstract: The approximate point-in-triangulation (APIT) localization algorithm was prone to in-to-out and out-to-in errors during the measurement using the optimal point-in-triangulation method, and it would has bad effect on positioning accuracy. In order to solve the problem, an improved APIT localization algorithm based on same side technique of vector product was proposed. A received signal strength indicator localization algorithm was used to realize the initial positioning of the node. And the same side technique of vector product was used to replace the inner point test method. Both of them improved the positioning efficiency. After the simulation on MATLAB, the positioning error data of APIT localization algorithm and the improved APIT localization algorithm were gotten. The results demonstrate that, on positioning accuracy, the improved APIT localization algorithm performs better than APIT algorithm.
-
Figure 6. To determine whether the unknown node is within the beacon triangle or not
a—inside b—outside
Figure 7. Positioning error of APIT and the improved APIT
a—node map b—positioning error of APIT c—positioning error of the improved APIT
Figure 8. Positioning error integration of APIT and the improved APIT
a—comparison of 61~175 positioning error b—comparison of 176~300 positioning error
-
[1] WU M, CHENG L L.Wireless sensor network node and realization method[J]. Instrument Technique and Sensor, 2008, 37(12):14-16(in Chinese). [2] LONG L, LI Z F. 3-D position measurement algorithm based on laser displacement sensors[J].Laser Technology, 2017, 41(4):531-536(in Chinese). [3] WU Ch, YUAN Y B, ZHANG M Y. Plane target positioning based on reflection intensity and K-means clustering method[J].Laser Technology, 2015, 39(3):341-343(in Chinese). [4] JIN R Ch, CHE Zh P, XU H, et al.RSSI-based localization algorithm for outliers suppression in wireless sensor networks.[J].Wireless Networks, 2015, 21(8):2561-2569. doi: 10.1007/s11276-015-0936-x [5] HE T, HUANG Ch D, BLUM B M, et al. Range-free localization schemes in large scale sensor networks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking, MOBICOM'2003.New York, USA: ACM Press, 2003: 81-95. [6] YAO Y, HAN Q, XU X, et al. A RSSI-based distributed weighted search localization algorithm for WSNs[J].International Journal of Distributed Sensor Networks, 2015, 11(4):1-11. [7] XIONG H, CHEN Z, AN W, et al. Robust TDOA localization algorithm for asynchronous wireless sensor networks[J].International Journal of Distributed Sensor Networks, 2015, 11(5):1-10. [8] YANG T Ch, JIN L, CHENG J.An improvement CHAN algorithm based on TOA position[J].Acta Electronica Sinica, 2009, 37(4):819-822(in Chinese). [9] MAO Y Y, LI M Y, ZHANG B J. AOA location algorithm based on RBF neural network[J].Journal of Computer Applications, 2008, 28(1):1-3(in Chinese). [10] ZENG Zh L, GAO J M, WANG J H.Corrected range weighted centroid localization algorithm based on RSSI for WSN[M].Melbourne, Australia:Information Systems and Computer Engineering, 2010:453-460. [11] TOMIC S, MEZEI I. Improvements of DV-Hop localization algorithm for wireless sensor networks[J].Telecommunication Systems, 2015, 61(1):93-106. [12] LIU Y, CHEN J, XU Z.Improved DV-Hop localization algorithm based on bat algorithm in wireless sensor networks[J].KSⅡ Transactions on Internet and Information Systems, 2016, 11(1):215-236. [13] KUMAR S, LOBIYAL D K.Novel DV-Hop localization algorithm for wireless sensor networks[J].Telecommunication Systems, 2016, 64(3):509-524. [14] LI X, YAN L, PAN W, et al. Optimization of DV-Hop localization algorithm in hybrid optical wireless sensor networks[J].Journal of Heuristics, 2014, 21(2):177-195. [15] AN W X, ZHAO J M, LI D A.Research of localization algorithm for wireless sensor networks based on Amorphous[J].Transducer and Microsystem Technologies, 2013, 32(2):33-35(in Chinese). [16] DOHERTY L, PISTER K S J, GHAOUI L E.Convex position estimation in wireless sensor networks[J].Infocom Twentieth Joint Conference of the IEEE Computer & Communications Societies, 2001, 3(3):1655-1663. -
点击查看大图
图(9)
计量
- 文章访问数: 5664
- HTML全文浏览量: 3500
- PDF下载量: 193
- 被引次数: 0
