网站地图
-
激光三角测距法作为一种传统的非接触式光电检测方法[1]，因其易实现、高精度、高效率以及优良的抗干扰能力和实时性等优点而被广泛地应用在工业生产的很多领域[2]。根据激光三角测距原理可知, 激光投射到被测物体表面，反射后成像于接收探测器光敏面[3], 光敏面上光斑成像质量的好坏决定系统的准确性，故系统光学参量的选取至关重要。近年来，相关学者在激光三角测距传感器的光学系统研究方面已经取得一定的成果, 但在光学系统参量的获取上仍延续着经验选取和实验论证的传统方法[4], 并未采用可行有效的算法，从而导致后期实验任务冗重。
本文中对于光学系统参量选取问题，提出一种基于粒子群的优化算法。在激光三角测距传感器数学模型的基础上，阐明工作距、工作角、成像透镜焦距、成像长度等参量对测量系统的影响规律, 采用粒子群优化算法对参量进行优化, 得到符合要求的参量值，即可缩短获取参量时间，又可达到较高精度，为后期传感器设计提供可靠的参考依据。
-
激光三角测距传感器作为一种非接触式光电检测设备[5]，其基本原理如图 1所示。当被测物体放置在参考位置O时，激光器发射出激光通过聚光镜，投射到被测物表面，反射后通过接收透镜成像于电荷耦合器件(charge-coupled device，CCD)光敏面。当被测物体沿激光发射方向相对位置O移动y时，则成像于CCD接收面的光斑相对像方参考位置P移动x。x和y之间满足透镜成像规律。因此，通过CCD接收面得到光斑的精确位移值x，由x和y之间满足的关系式即可得到被测物的精确位移值y，从而实现了测量待测物位移的目标。
Figure 1. Working principle and imaging model
由工作原理可知，工作距a与像距b应满足近轴透镜成像公式。工作角α与成像角β应满足恒聚焦关系。则被测物的位移y与光斑位移x满足关系式[6]：
$ \mathit{\boldsymbol{y}} = \frac{{a\mathit{\boldsymbol{x}}{\rm{sin}}\beta }}{{b{\rm{sin}}\alpha - \mathit{\boldsymbol{x}}{\rm{sin}}(\alpha + \beta ){\rm{ }}}} $
(1) $ \mathit{\boldsymbol{x}} = \frac{{b\mathit{\boldsymbol{y}}{\rm{sin}}\alpha }}{{a{\rm{sin}}\beta + \mathit{\boldsymbol{y}}{\rm{sin}}(\alpha + \beta ){\rm{ }}}} $
(2) $ {\rm{tan}}\beta = \frac{{a - f}}{f}{\rm{tan}}\alpha $
(3) 由(1)式可得，当物体沿激光发射方向远离激光器时，y>0mm，其最大值为可测量最远距离，定义为ymax；当物体沿激光发射方向靠近激光器时，y < 0mm，其最小值为可测量最近距离，定义为ymin，则系统的测量范围为[ymin, ymax]。根据透镜成像规律可知，与x向相反方向移动，故位移x与y满足关系(2)式[7]。工作角α与成像角β满足(3)式的恒聚焦关系[7]。
-
本系统中选用的接收探测器为线阵CCD TCD1711，其有效像素数目为7450个，像素尺寸为4.7μm×4.7μm，则有效地成像长度为4.7μm×7450，即为35.015mm。
根据经验可知，光斑若成像在CCD的边缘位置会影响测量准确度，为了减小测量误差，将CCD的边缘部分有效像素舍弃，取像素数量的使用系数η=0.9，又假定测量原点在CCD中间，所以CCD成像像素空间为：(－7450×0.9/2, 7450×0.9/2)，则CCD测量范围为(－15.757mm, 15.757mm)。
-
测量系统的测量灵敏度[7]为：
$ S = \frac{{{\rm{d}}\mathit{\boldsymbol{x}}}}{{{\rm{d}}\mathit{\boldsymbol{y}}}} = \frac{{ab{\rm{sin}}\alpha {\rm{sin}}\beta }}{{{{[a{\rm{sin}}\beta + \mathit{\boldsymbol{y}}{\rm{sin}}(\alpha + \beta )]}^2}}} $
(4) 从(4)式可以看出，灵敏度的大小与参量(a, b, α, β, f)及被测物位移y有关。根据(4)式可以得出，灵敏度S的最小值发生在位移y取正值最大值即ymax处，把最小的灵敏度记为Smin，作为衡量测量系统精度的主要标准，在接下来的分析中提到的灵敏度均为Smin。
-
系统分辨力由CCD两相邻像素中心距离大小决定，则本文中系统的分辨力为CCD中心位置的两像素中心距离对应的被测物位移差[8]，即:
$ \begin{array}{l} k = \frac{{0.0047 \times a{\rm{sin}}\beta }}{{b{\rm{sin}}\alpha - 0.0047 \times {\rm{sin}}(\alpha + \beta )}} + \\ \frac{{0.0047 \times a{\rm{sin}}\beta }}{{b{\rm{sin}}\alpha + 0.0047 \times {\rm{sin}}(\alpha + \beta )}} \end{array} $
(5) -
根据接收探测器CCD测量范围可知，成像在CCD两端的最大像点对应的被测物位移为：
$ {y_{{\rm{max}}}} = \frac{{15.757 \times a{\rm{sin}}\beta }}{{b{\rm{sin}}\alpha - 15.757 \times {\rm{sin}}(\alpha + \beta ){\rm{ }}}} $
(6) $ {y_{{\rm{min}}}} = \frac{{15.757 \times a{\rm{sin}}\beta }}{{b{\rm{sin}}\alpha + 15.757 \times {\rm{sin}}(\alpha + \beta )}} $
(7) 由此可得系统的测量量程$R = {y_{{\rm{max}}}} - {y_{{\rm{min}}}} $。此外，系统的水平宽度$ L = \left( {a + b} \right){\rm{sin}}\alpha $，反映了系统体积的大小。
-
当工作角α=30°和成像透镜焦距f=40mm时，工作距a在(50mm，150mm)范围内逐渐增大，可得各系统指标与工作距之间的关系，如图 2所示。
Figure 2. Relationship between each index and working distance
-
当工作距a=100mm和成像透镜焦距f=40mm时，工作角α在(20°, 60°)范围内逐渐增大，可得各系统指标与工作角之间的关系，如图 3所示。
Figure 3. Relationship between each index and working angle
-
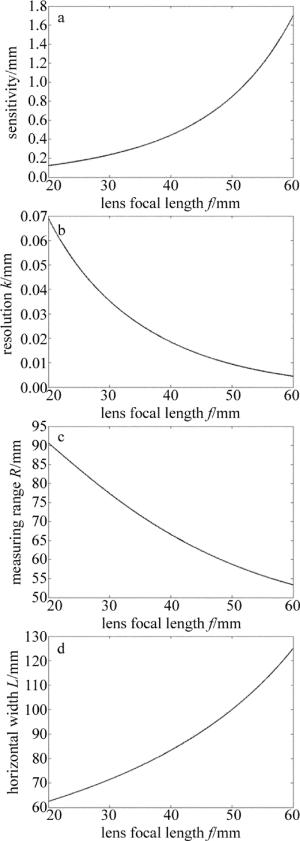
当工作距a=100mm和工作角α=30°时，成像透镜焦距f在(20mm，60mm)范围内逐渐增大，可得各系统指标与成像透镜焦距之间的关系，如图 4所示。
Figure 4. Relationship between each index and focal length of image lens
综合上述分析可知，接收探测器的灵敏度S与工作距的变化曲线趋势相反，与工作角和透镜焦距的变化趋势相同，但对工作角及透镜焦距取值时需考虑到实际物体体积，系统分辨能力的变化趋势与灵敏度相同，与测量量程变化趋势相反；水平宽度的变化趋势则与变化量的变化趋势完全相同，随着工作距、工作角和透镜焦距的变大，系统水平宽度均变大。
若使系统灵敏度和分辨力较好，根据其关系可知，工作角和透镜焦距将取到较大值，但设计传感器时为了操作方便，需将整个系统集成，故对工作角α和透镜焦距f的取值不可过大。而系统分辨力的变化趋势和测量量程相反；同时，系统水平宽度过大，则会造成系统体积过大。所以，在进行参量选取时，应根据自己实际需求，同时兼顾各个系统指标，选取合适的参量。
-
激光三角测距传感器的光学参量较多且相互牵制，目前大多数学者仅采用实验方法选择参量，参量选取精度较低，从而大大增加了后期实验部分的工作。因此，本文中在对光学参量深入分析的基础上采用粒子群优化算法(particle swarm optimization，PSO)，同时结合本系统所需，获取符合要求的参量，为后期传感器的设计提供指导依据。
-
粒子群优化算法是一种新的进化算法[9]。首先对一群粒子进行随机初始化，然后找到搜索空间的最优粒子并追随，即不断地更新迭代直到找到最优解[10]。在迭代时，粒子通过追寻两个最优解来进行速度和位置更新，其更新公式如下所示[11]：
$ \begin{array}{l} {\mathit{\boldsymbol{v}}_{ij}}\left( {t + 1} \right) = \omega \times {\mathit{\boldsymbol{v}}_{ij}}\left( t \right) + {c_1} \times {r_1} \times \left[ {{p_{ij}} - {x_{ij}}\left( t \right)} \right] + \\ {c_2} \times {r_2} \times \left[ {{p_{{\rm{g}}, j}} - {x_{ij}}\left( t \right)} \right], \\ {x_{ij}}\left( {t + 1} \right) = {x_{ij}}\left( t \right) + {\mathit{\boldsymbol{v}}_{ij}}\left( {t + 1} \right) \end{array} $
(8) 式中, i为第i个粒子，i=1, 2, …, N, 其中N为粒子群的个数；j为第j维，j=1, 2, …, d，其中d为粒子维数；pij为个体极值，为粒子个体本身所找到的最优解；pg, j为全局极值，为当前整个粒子群找到的最优解[12]，用于pg, j表示全局极值；t为迭代次数；ω为惯性权重；c1和c2为学习因子；r1和r2为0到1之间均匀分布的随机数[13]。
由于本文中的激光三角测距传感器的测量量程要求为10mm，故需在粒子群优化算法的基础上加入测量量程的约束条件。目前罚函数法在处理约束问题时应用最广泛，因此, 本文中采用罚函数法来处理对测量量程的约束。
罚函数法所构造的广义目标函数形式如下[14]：
$ F\left( x \right) = f\left( x \right) + h\left( k \right)H\left( x \right), \left( {x \in Q \subset {E^n}} \right) $
(9) 式中, f(x)是约束优化问题的原始目标函数；h(k)H(x)为惩罚项；h(k)为惩罚系数；H(x)是多级分配惩罚函数，Q为优化设计变量空间，E为实数集，n为优化设计变量个数。
-
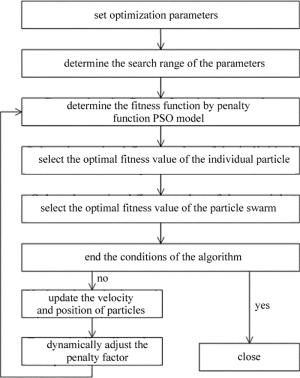
基于罚函数的粒子群优化参量的计算流程如图 5所示。通过试算，确定粒子群算法的参量如下：粒子个数为20，粒子维数为3维，迭代次数为300，惯性权重[15]ω=0.6，学习因子c1=c2=1.7，初始惩罚系数h0=0.1，迭代中转步为100，惩罚系数增大倍率m=1.4，确定参量工作距a优化空间为(50mm, 150mm), 工作角α的优化空间为(20°, 40°)，焦距f的优化空间为(20mm，40mm)。根据(4)式定义原始目标函数：
$ f\left( x \right) = \frac{{{x_1}^2 \times {x_3} \times {\rm{sin}}{x_2} \times {\rm{sin}}\beta }}{{{{[{x_1}{\rm{sin}}\beta + {y_{{\rm{max}}}}{\rm{sin}}({x_2} + \beta )]}^{2}}}} $
(10) 
Figure 5. Flow chart of parameter optimization
式中, β的参量关系由x1, x2, x3表示。
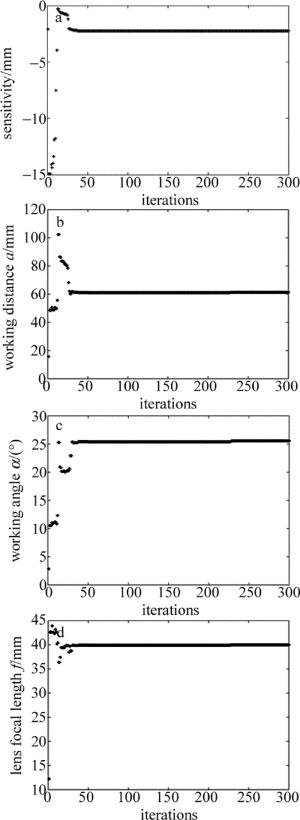
采用粒子群优化算法得到一组优化结果，函数迭代图如图 6所示，所有参量结果如表 1所示。
Figure 6. Function iteration graph
Table 1. The optimized results
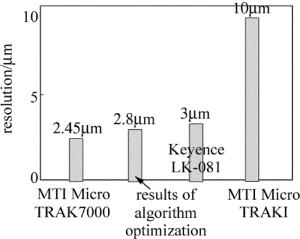
parameter optimization result S 2.2386mm k 0.0028mm a 61.2862mm b 115.1680mm α 25.2900° β 14.2971° f 40.0000mm 通过粒子群算法进行参量优化，在灵敏度最大和测量量程一定的要求下，确定粒子的搜索空间，得出满足本系统所需的最优解。优化结果得出的最小灵敏度Smin达到2.2386mm时，系统分辨力可达2.8μm，由图 7可知，相对市场上的部分产品，利用粒子群优化得到的分辨力可达到较高水平，此时工作距a=61mm时，像距b=115mm。由于激光发射和成像部分要组装到一起，像距过大会导致系统体积过大，因此在像距部分放置平面镜，以光反射原理为基础，使光斑成像在CCD接收面上，从而减小系统体积。工作角α角越大及透镜焦距f越大，灵敏度越大，在考虑要同时兼顾灵敏度和系统体积的基础上，取α=25°，取f=40mm，此时成像角β=14°。在所要求的搜索空间内，粒子群算法优化结果基本符合本系统要求，可作为后期实验时的重要参考。
Figure 7. Comparison of resolution
-
从测量原理出发，对激光位移传感器光学参量进行建模分析，并采用粒子群算法进行优化，获取符合本系统要求的最优参量，通过MATLAB优化发现该算法在高精度高效率情况下能够得到三角测距最优参考值，对激光三角测距法具有一定的指导意义。但整个分析实验均为理想情况下，并未考虑器件、环境及人为等因素造成的误差及影响。因此在进行实际测量时，需根据实际情况做适当调整，并采取相应手段尽可能消除干扰，补偿器件造成的误差。
基于粒子群算法的激光位移传感器参量优化
Parameter optimization of laser displacement sensor based on particle swarm optimization algorithm
-
摘要: 为了提高激光三角测距精度、优化传感器设计过程中的光学参量，采用数学建模和计算机辅助分析的方法，解析了激光三角测距传感器中的关键参量与测量系统各指标的关系，并采用一种基于粒子群算法的参量优化方法，得到符合系统优化要求的光学参量，进行了理论分析和验证。结果表明，在进行参量设计时，各参量相互牵制；确定了粒子群搜索空间和约束；在灵敏度Smin达到2.2386mm时，系统分辨力可达到2.8μm，且其它各参量取值符合系统要求，同时优化效率大大提高。该优化方法算法简单、操作方便。Abstract: In order to improve the precision of laser triangulation sensor and optimize the optical parameters of design process, through mathematical modeling and computer-aided analysis method, the relationship between key parameters of laser triangulation sensor and each index of measurement system was analyzed. A method of parameter optimization based on particle swarm algorithm was adopted. After theoretical analysis and experimental verification, the parameters to meet the requirements of optical system optimization were gotten. The results show that, the parameter is controlled by each other during designing. Search spaces and constraints of particle swarm are determined. When sensitivity Smin reaches 2.2386mm, the resolution of system can reach 2.8μm. Other parameters meet the system requirements, and the optimization efficiency is greatly improved. The optimization method is simple and convenient to operate.
-
Figure 2. Relationship between each index and working distance
a—sensitivity b—resolution c—measurement range d—horizontal width
Figure 3. Relationship between each index and working angle
a—sensitivity b—resolution c—measurement range d—horizontal width
Figure 4. Relationship between each index and focal length of image lens
a—sensitivity b—resolution c—measurement range d—horizontal width
Figure 6. Function iteration graph
a—sensitivity b—working distance c—working angle d—lens focal length
Table 1. The optimized results
parameter optimization result S 2.2386mm k 0.0028mm a 61.2862mm b 115.1680mm α 25.2900° β 14.2971° f 40.0000mm 
下载: 导出CSV
-
[1] WU W, YAN L P.Laser displacement ranging system based on PSD[J]. Microcontrollers & Embedded Systems, 2016, 16(1):49-52(in Chinese). [2] WANG X J, GAO J, WANG L. Survey on the laser triangulation[J]. Chinese Journal of Scientific Instrument, 2004, 25(4):601-604(in Chinese). [3] WU J B, LUO Q M.Biomedical applications of laser triangulation[J]. Laser Technology, 2006, 30(1):1-4(in Chinese). [4] ZHU Y X, ZHAO J, WANG Y L. Model establishment and parameter optimization of high precision laser ranging system[J]. Machinery, 2016, 54(7):68-71(in Chinese). [5] DEMEYERE M, RURIMUNZU D, EUGENE C. Diameter measurement of spherical objects by laser triangulation inall ambulatory context[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(3):867-872. doi: 10.1109/TIM.2007.894884 [6] JIN W Y, ZHAO H, TAO W. Modeling of laser triangulation sensor and parameters optimization[J]. Chinese Journal of Sensors and Actuators, 2006, 19(4):1090-1093(in Chinese). [7] SEN W X, FENG P, KE X, et al. Melt level measurement for the CZ crystal growth using an improved laser triangulation system[J]. Measurement, 2017, 103(5):27-35. [8] EHLERT D, HORN H J, AME R. Measuring crop biomass density by laser triangulation[J]. Computers and Electronics in Agriculture, 2008, 61(2):117-125. doi: 10.1016/j.compag.2007.09.013 [9] XIE Zh J, ZHENG L J, QU Zh G.Improved PSO algorithm based PID controller of permanent magnet synchronous motor[J]. Modern Electronics Technique, 2017, 40(7):139-142(in Chinese). [10] WANG D F, MENG L. Performance analysis and parameter selection of PSO algorithms[J]. Acta Automatica Sinica, 2016, 40(10):1552-156(in Chinese). [11] DAI C, WANG Y Q, XUE F. 3-D lidar echo decomposition based on particle swarm optimization[J]. Laser Technology, 2016, 40(2):284-287(in Chinese). [12] RIWANTO B A, TIKKA T, KESTILA A. Particle swarm optimization with rotation axis fitting for magnetometer calibration.IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2):1009-1022. doi: 10.1109/TAES.2017.2667458 [13] LIU Zh X, LIANG H.Parameter setting and experimental analysis of the random number in particle swarm optimization algorithm[J]. Control Theory & Applications, 2010, 27(11):1489-1496(in Chinese). [14] ZHANG L P, YU J H, HU Sh X. Optimal choice of parameters for particle swarm optimization[J]. Journal of Zhejiang University Science A(Science in Engineering), 2005, 6A(6):528-534. [15] ZHANG G Y, WU Y J. Multi-constraint optimization algorithm based on multistage punish function and particle swarm optimization[J]. Journal of Beijing Institute of Petrochemical Technology, 2008, 16(4):30-32(in Chinese). -
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 9027
- HTML全文浏览量: 6639
- PDF下载量: 231
- 被引次数: 0
