网站地图
-
激光输能是一种将光能转化为电能的无线能量传输方式，与传统的有线输电线路相比，具有不需高成本输电线路、不受地形影响、可进行空对空、空对地、地对地间的能量传输等优点，在解决空间航天器、临近空间飞行器、高空飞艇以及无人机能源供应等问题方面具有巨大的应用前景[1-3]。光电池是激光输能过程中将光能转化为电能的转换装置，其转换效率的高低是激光输能技术的重要指标，光电转换效率的影响因素有很多，例如辐照强度、温度和电池自身材料等，其中温度是影响转换效率的重要因素[4]。激光辐照光电池会产生温升效应，导致温度上升并引起电池工作性能的改变，从而降低光电转换效率，这是限制激光输能技术实际应用的瓶颈之一。因此，为了研究光电池温升效应对电池工作性能及转换效率的影响，国内外学者对光电池的温度场进行了大量数值模拟研究。
参考文献[5]中利用ANSYS CFD有限元软件结合热模型和电模型分析了太阳光辐照下光电池板表面在有、无冷却条件下的温度场分布。参考文献[6]中仿真分析了光电池厚度方向上各层不同材料间的温升规律。参考文献[7]和参考文献[8]中基于COMSOL Multiphysics软件分别对连续激光和脉冲激光辐照下GaAs材料的温度场分布进行了数值模拟计算。参考文献[9]中采用有限差分数值计算了连续激光辐照半导体材料温度场，并用MATLAB软件数值模拟了材料的温升过程。国内外研究大多是针对太阳光辐照下光电池的温度场变化，而激光辐照下温度场研究较多针对的是半导体材料而不是对光电池，激光辐照下光电池的温度场研究较少，且以往研究太阳光辐照下的光电池温度场分布通常把光电转换效率和热源当作常值，但光电转换效率在激光辐照下随温度变化幅度很大，不能忽略激光热源的变化，因此，需要解决激光辐照下光电池的光电转换效率和激光热源随温度变化的问题。
针对激光辐照下光电池的温度场分析问题，本文中结合COMSOL Multiphysics多物理场耦合软件和MATLAB软件对光电池的温度场进行数值模拟计算。分析了光电池能量传递过程，在建立光电池2维物理模型和热模型基础上，通过COMSOL Multiphysics与MATLAB软件进行联合仿真，解决了激光热源随光电转换效率变化下光电池温度场的仿真问题，并对电池温度场随激光参量(辐照时间、功率密度、光斑面积、入射角)的变化进行了仿真分析，得出了电池温度场特性与变化规律。
-
在建立光电池物理模型和热模型基础上，用COMSOL软件对激光辐照下的光电池温度场进行数值模拟。
-
本文中假设激光输能的接收装置采用硅光电池，尺寸为20mm×20mm×0.2mm，实际光电池结构是由正面金属栅线电极、减反射膜、硅半导体层以及背面金属电极组成，这是由于硅半导体自身的导电性能较差以及对光的反射率大，单独制作成光电池时对光能的利用率很低，因此，为增强电池的导电性，在硅半导体上、下两个面分别烙印正面金属栅线电极和背面金属电极，正面栅线电极材料一般为银，厚度约为0.003mm，背面电极材料通常为铝，厚度约为0.01mm；为减少光的反射，在硅上表面镀上一层减反射膜，材料一般为SiO2, 厚度约为10-4mm。由于硅半导体厚度相比其它材料大很多，综合考虑计算精度和计算时间，本文中利用修正的热物性参量的硅半导体材料层近似代替硅光电池。当激光束垂直照射光电池中心处时，高斯激光束和光电池近似为轴对称结构，因此，本文中取光电池的轴对称面进行研究，简化的2维物理模型如图 1所示。
Figure 1. Physical model of silicon photovoltaic cell irradiated by laser
图 1中坐标原点O位于光电池表面中心位置，x方向表示平行于光电池边缘的方向(由内指向外)，y方向表示光电池的厚度方向，即对称轴；a表示激光光斑半径，b表示光电池边缘长度的1/2，w表示光电池的厚度。
-
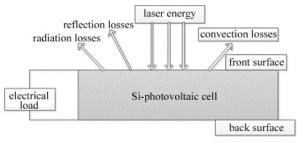
激光光束照射到光电池时，入射激光能量传递形式如图 2所示。除了被反射的能量和通过热辐射、热对流损失的能量，以及硅半导体材料经光生伏特效应将光能转化为电能外，其余能量转化为了热能。因此，考虑电池内部温升时，需要把电池光电转换消耗的能量计算进去。
Figure 2. Transfer form of incident laser energy
-
连续激光辐照下硅半导体材料的温度分布可通过求解Fourier热传导偏微分方程得到，在图 1所示坐标系下的光电池2维热传导方程表达式为[10]：
$ \begin{array}{*{20}{c}} {\rho c\frac{{\partial T\left( {x,y,t} \right)}}{{\partial t}} = }\\ {\frac{\partial }{{\partial x}}\left( {\kappa \frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\kappa \frac{{\partial T}}{{\partial y}}} \right) + Q\left( {x,y,t} \right)} \end{array} $
(1) 式中, ρ为材料的密度, c为材料的比热容，κ为材料的热导率，T为光电池温度，t为时间，Q为热源项。
考虑激光在电池内部的传播，能量除转化为电能外，其余转化为热能，则模型的热源项Q表达式为：
$ Q = \alpha \left( {1 - \eta } \right){\varphi _0}\exp \left( { - 2\frac{{{x^2}}}{{{a^2}}}} \right)\exp \left( { - \alpha y} \right) $
(2) 式中, α为材料的吸收系数，η为激光辐照下光电池的转换效率，φ0为激光中心功率密度。
考虑光电池的光电转换效率随电池工作温度的增加而降低，引起热源项Q的不断变化，下面建立激光辐照下的光电池转换效率模型。
-
激光辐照下, 光电池的转换效率定义为光电池外部回路连接最佳负载电阻时的输出功率(即最大输出功率)在输入功率中所占比重[11]，光电转换效率的表达式为：
$ \eta = \frac{{{P_{{\rm{out,max}}}}}}{{{P_{{\rm{in}}}}}} = \frac{{{I_{{\rm{op}}}}{V_{{\rm{op}}}}}}{{\varphi {\rm{ \mathsf{ π} }}{a^2}}} $
(3) 式中, Pout, max为最大输出功率，Pin为入射激光功率，Iop和Vop分别为最佳输出电流和最佳输出电压, φ为激光功率密度。
Iop和Vop可通过光电池输出电流I与输出电压V的关系式求得[12]:
$ I = {I_{{\rm{ph}}}} - {I_{\rm{s}}}\left\{ {\exp \left[ {\frac{{e\left( {V + I{R_{\rm{s}}}} \right)}}{{nkT}}} \right] - 1} \right\} - \frac{{I{R_{\rm{s}}} + V}}{{{R_{{\rm{sh}}}}}} $
(4) 式中, Iph为光生电流，Is为反向饱和电流，n为二极管理想因子，k为玻尔兹曼常数，e为单位电荷，Rs为等效串联电阻，Rsh为等效并联电阻。
求解Iph表达式：短路条件下短路电流为ISC，则有I=ISC，V=0, 而流经二极管的反向饱和电流极小，可忽略不计，则有：
$ {I_{{\rm{ph}}}} = {I_{{\rm{SC}}}}\left( {1 + \frac{{{R_{\rm{s}}}}}{{{R_{{\rm{sh}}}}}}} \right) $
(5) 参考文献[13]中给出了激光辐照下光电池短路电流为：
$ {I_{{\rm{SC}}}} = E\left( T \right)\varphi {\rm{ \mathsf{ π} }}{a^2}\frac{\lambda }{{1240}} $
(6) 式中, E(T)为内量子效率, λ为激光波长。
E(T)表示入射到光电池内部的光子产生一个对外电路有贡献的电子的概率。由于温度变化会引起内量子效率的变化，本文中引入温度修正因子KT, 令KT=kT(T-T0)则有：
$ \begin{array}{*{20}{c}} {E\left( T \right) = E\left( {{T_0}} \right)\left( {1 + {K_T}} \right) = }\\ {E\left( {{T_0}} \right)\left[ {1 + {k_T}\left( {T - {T_0}} \right)} \right]} \end{array} $
(7) 式中, T0为常温值，E(T0)为常温下的内量子效率，kT为内量子效率的温度系数。
考虑光电池表面对光的反射，假设反射系数为R，综合上述公式得光生电流表达式为Iph：
$ \begin{array}{*{20}{c}} {{I_{{\rm{ph}}}} = \left( {1 - R} \right)\varphi {\rm{ \mathsf{ π} }}{a^2}E\left( T \right)\frac{\lambda }{{1240}} \cdot }\\ {\left( {1 + \frac{{{R_{\rm{s}}}}}{{{R_{{\rm{sh}}}}}}} \right)\left[ {1 + {k_T}\left( {T - {T_0}} \right)} \right]} \end{array} $
(8) 参考文献[14]中给出了反向饱和电流随温度变化的关系式为：
$ {I_{\rm{s}}} = {I_{\rm{r}}}{\left( {\frac{T}{{{T_0}}}} \right)^{\frac{3}{n}}}\exp \left[ {\frac{{e{E_{\rm{g}}}\left( {T - {T_0}} \right)}}{{nk{T_0}T}}} \right] $
(9) 式中, Ir为常温下的反向饱和电流，Eg为硅材料的禁带间隙。
光电池的转换效率可通过(3)式、(4)式、(8)式、(9)式联立求解。式中除变量T外，其它参量都可看作常值, 具体数值在表 1中给出。由于输出电流和输出电压为非线性关系[15]，而且求解光电转换效率需找到最佳的输出电流和输出电压，三者还与温度值T有关，其中关系比较复杂，因此，本文中利用MATLAB软件对非线性方程强大的数值计算能力来求解光电转换效率，再利用COMSOL和MATLAB进行联合仿真，计算激光热源随光电转换效率不断变化情况下的光电池温度场分布。下面给出COMSOL与MATLAB联合仿真的数值模拟过程。
Table 1. Efficiency parameters of photoelectric conversion
parameter value of expression the Boltzmann constant k 1.3806505×10-23J·K-1 unit charge e 1.6022×10-19C diode ideal factor n 2 internal quantum efficiency at room temperature E(T0) 0.95 internal quantum temperature coefficient kT 8×10-4 reverse saturation current at room temperature Ir 8×10-6A laser spot radius a 102mm laser wavelength λ 980nm laser power density φ 2000W·m-2 parallel resistance Rsh 106Ω series resistance Rs 0.1Ω band gap Eg 1.13eV reflectivity R 0.1 -
为简化复杂边界条件下的光电池热传导问题，用软件进行数值模拟时通常假设边界条件和设定参量，进而求解光电池的温度场分布。
-
第1节中(3)式、(4)式、(8)式、(9)式中给出了固定参量下的转换效率与温度的关系式，由于转换效率与温度是非线性关系，本文中用MATLAB软件分别定义了(4)式、(8)式、(9)式的函数表达式，由(4)式用优化算法计算出最佳输出电流和最佳输出电压，再由(3)式得出转换效率与温度的函数关系式η(T)。
COMSOL Multiphysics软件内置有MATLAB函数接口，当用COMSOL软件完成物理模型的建立及参量设定，并对模型进行网格划分后，开始仿真计算，其基本流程是：对给定的初始条件进行计算，得到初始温度场分布；求解热传导过程，用MATLAB计算t=t1时刻的转换效率η(T1)，更新热源Q(T1)，得出新的温度场分布；继续求解热传导过程，得到下一时刻t=t2对应的η(T2)和Q(T2)，更新温度场分布；再下一时刻重复上述求解步骤，反复迭代计算，当η(T) < 0时停止调用MATKAB函数η(T)，当时间达到设定的条件t>100s时求解结束。仿真计算流程如图 3所示。
Figure 3. Flow chart of numerical simulation
-
光电转换效率利用MATLAB软件在给定影响参量情况下求得，参考已有光电池和激光实物数据，设定的光电转换效率影响参量如表 1所示。
表 1中激光参量包括激光功率密度φ、激光光斑半径a，在仿真分析光电池温度场分布是可变的，其余参量为不可变的固定值。
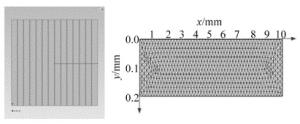
由第2节可知，仿真计算时取光电池轴对称面的2维结构作为计算区域，其网格划分如图 4所示。左边小图中的直线表示实际光电池的网格剖分位置。假定边界条件见下。
Figure 4. Mesh generation for 2-D physical model
初始条件满足:
$ T\left| {_{t = 0}} \right. = 298{\rm{K}} $
(10) 硅光电池侧表面绝热满足:
$ \frac{{\partial T}}{{\partial x}}\left| {_{x = b}} \right. = 0 $
(11) 电池上表面与空气之间的自由对流以及上下表面向周围环境的热辐射满足[7, 16]:
$ \begin{array}{*{20}{c}} {\kappa \frac{{\partial T}}{{\partial y}}\left| {_{y = 0}} \right. = h\left[ {{T_0} - T\left( {x,t} \right)} \right] + }\\ {\left( {{\varepsilon _{\rm{f}}} + {\varepsilon _{\rm{b}}}} \right)\sigma \left[ {T_0^4 - T'\left( {x,0,t} \right)} \right]} \end{array} $
(12) 式中, h是表面传热系数，εf和εb分别为上、下表面的辐射率，σ为斯特藩常量，T′为环境温度，假定与初始温度T0相同。
利用COMSOL软件进行光电池内部热传递仿真模拟时，需要对光电池材料的热物性参量进行设定，本模型采用硅半导体材料替代光电池结构，结合光电池其它材料实际的参量，设定的热物性参量如表 2所示。
Table 2. Thermal physical property of silicon photovoltaic cells
parameter value of expression thermal conductively κ 150W·m-1·K-1 density ρ 2400K·m-3 specific heat capacity c 700J·kg-1·K-1 surface coefficient of heat transfer h 5W·m-2·K-1 thermal radiation rate εf 0.95 thermal radiation rate εb 0.9 absorption coefficient α 0.9 initial temperature T0 298K COMSOL与MATLAB联合仿真时做如下假设：(1)光电池材料热物性参量不随温度变化而改变；(2)MATLAB计算光电转换效率时激光功率密度等于激光中心功率密度；(3)考虑高斯激光束在光电池表面温度分布不均匀，即温度值T不同，但由于电池尺寸小，中心与边缘温度差值不大，假定COMSOL返回给MATLAB的温度T值为电池中心温度值。
-
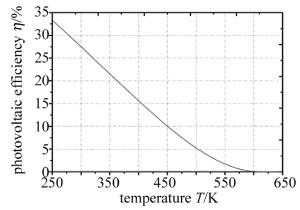
用MATLAB按表 1中的参量设定值求得光电转换效率和电池温度的关系如图 5所示。
Figure 5. Relationship between photoelectric efficiency and cell temperature
从图 5可看出，光电转换效率在初始温度值最高，达到31%，随着温度增加，转换效率大致呈线性减小，当温度超过600K时，光电转换效率变为零，而硅半导体材料的发生光生伏特效应的极限温度值620K[17]，因此，模型具有合理性。
当表 1中激光功率密度φ和T参量值分别变化时，其余参量不变，用MATLAB分别求得转换效率和电池温度、转换效率和激光功率密度的关系如图 6、图 7所示。
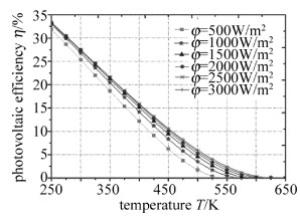
Figure 6. Relationship between photoelectric efficiency and temperature under different laser power densities
Figure 7. Relationship between photoelectric efficiency and laser power density under different temperature
从图 6可看出，不同激光功率密度下的光电转换效率与温度的关系曲线斜率大致相同，即温度增加幅度相同时，不同激光功率密度下的转换效率下降幅度相同；相同温度条件下，在一定范围内的激光功率密度越大，光电转换效率越大。从图 7可看出，电池温度越高，光电转换效率越低，但从各条曲线来看，光电转换效率随激光功率密度增加会先升高，当激光功率密度增加到约2000W/m2后，光电转换效率开始下降。
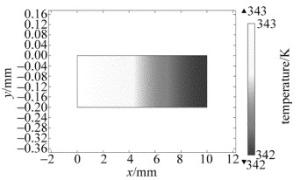
根据图 1所示物理模型和MATLAB采用表 1中参量值求解得到的光电转换效率与温度关系，利用COMSOL Multiphysics软件仿真计算激光功率密度为2000W/m2时的光电池温度场分布如图 8所示。横坐标x表示光电池沿径向的方向，纵坐标y表示厚度方向，右侧的色条表示不同颜色各自对应的温度值。综合考虑计算工作量和精度，设定的仿真时间为100s，时间间隔为0.1s。
Figure 8. Temperature field distribution of 100s
100s时，光电池的最高温度为343K，最高温度点位于光电池中心处，最低温度点在电池边缘为342K，最大温度差ΔT=1K。温度场分布与高斯激光束中心强度高，四周强度低的特性保持一致。当激光光斑全部覆盖电池表面时，由于电池的面积较小，导致电池温度梯度小，电池中心与边缘温度差值不大，因此，上节中所作假设(3)成立。下面研究光电池温升规律都是针对光电池中心点。
当t=100s时，由于电池厚度较薄(仅0.2mm)，y方向的温度梯度为零，电池表面温度等于对应内部温度值。当t=0.1s时，x=0对应的y轴上电池温度相同，因此，电池的厚度方向在极短时间内就达到热平衡，温度的差异主要表现在x方向。
-
下面分析不同激光参量对硅光电池温度场分布的影响。
-
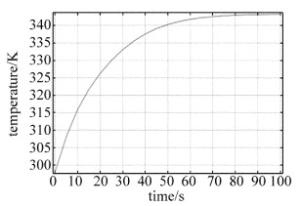
取光电池表面中心点进行仿真分析，按表 1中的参量设定，激光功率密度为2000W/m2时, 其温度随时间变化的关系如图 9所示。
Figure 9. Relationship between temperature of the center point and the irradiation time
从图 9中可以看出，随着时间的累积，光电池中心温度先保持较大温升速度增加，后缓慢增加，最后趋近于一个定值。这是由于电池的初始温度较低(298K)，开始阶段光电池与周围环境的热交换以吸收激光能量为主，向外辐射的能量少，温度上升快；当温度逐渐升高时，电池向外辐射的能量同时增加，直到电池吸收的激光能量等于向外辐射的能量，此时光电池达到热平衡状态。由图 3可知，当电池温度稳定在343K时，电池的转换效率从常温下的30%下降到22.4%，因此，激光辐照过程中需对电池进行降温处理，使电池一直保持高效率的工作状态。
-
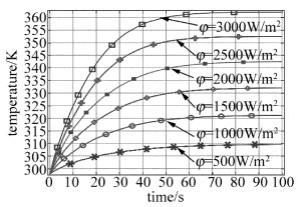
参考文献[18]中指出波长为1064nm、功率密度为1.13×107W/m2的激光辐照硅光电池时不会对电池表面造成损伤，本节中设定的激光功率密度均小于上述值，因此，电池的工作性能不会改变。图 10中给出了不同激光功率密度下电池中心点处的温升情况(表 1中激光功率密度参量φ值变化，其余参量不变)。
Figure 10. Relationship between temperature at center point and time under different power density
从图 10可以看出，不同激光功率密度下电池中心温度上升的曲线斜率不同，激光功率密度越大，温升速度越快，达到热平衡态时的温度值越高。当激光功率密度为500W/m2时，电池吸收的能量少，温升幅度小，而且温度上升速度慢，向外热辐射的量在短时间内与吸收的能量保持一致，电池达到热平衡态所需时间短；随着激光功率密度增加，入射到电池表面的激光能量越多，当激光功率密度为3000W/m2时，电池吸收能量的多，温度上升幅度大，温升速度快，电池对外辐射出的能量需要较长时间才能与吸收的能量相等，因此，电池达到热平衡态所需时间长。
激光输能过程中高激光功率密度容易产生高温，导致光电转换效率降低。而当激光功率密度较低时，虽然电池温度也较低，但从图 7可知，电池的光电转换效率不一定最高。因此，在负载对输出功率要求不高时，综合考虑温度和激光功率密度的影响，选用激光功率密度为2000W/m2进行激光输能比较合适，其它激光参量按表 1所示时能获得最佳的转换效率。
-
在COMSOL软件建立的2维物理模型中，激光光斑面积对光电池温度场的影响等效为激光光斑半径对电池温升的影响。研究激光光斑半径对电池温度场的影响可分为：(1)相同激光功率密度下不同光斑半径对电池温度场的影响，由Pin=φπa2可知，此时入射到电池表面的激光功率改变；(2)相同入射激光功率下不同光斑半径对电池温度场的影响，由φ=Pin/(πa2)可知，电池表面的激光功率密度改变。后者与上节分析激光功率密度对电池温升的影响不同，上节中分析的前提是激光光斑半径一定，且光斑全部覆盖电池表面，而后者光斑半径是变化的。下面将分别对两种情况进行研究。
图 11中给出了激光功率密度为2000W/m2下不同激光光斑半径对电池中心温升规律。
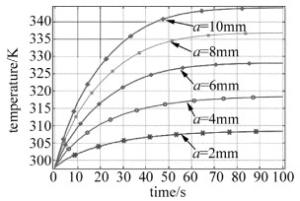
Figure 11. Relationship between temperature and time under different laser spot radius under the same φ
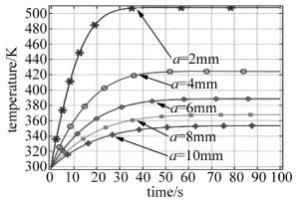
从图 11可以看出，当激光辐照功率密度为2000W/m2时，在相同辐照时间下，激光光斑半径越大，电池温升速度越快，温度上升幅度越大。相同激光功率密度条件下，由于激光光斑半径减小，入射到电池表面总的激光能量降低，电池能吸收的激光能量减少，导致温度上升速度变慢，温升幅度也减小。但在实际应用中激光器发射出的激光束照射到电池表面时，改变光斑半径，激光功率密度也会随之变化，难以保证激光功率密度一定，往往是在一定入射激光功率下来调整激光光斑的大小。下面给出入射激光功率为0.8W时不同激光光斑半径对电池中心温升的影响，如图 12所示。
Figure 12. Temperature field distribution under different laser spot radius under the same Pin
从图 12可以看出，在相同辐照时间下，激光光斑半径越小，电池温升速度越快，温度上升幅度越大，而且电池达到热平衡态时间越短。相同入射激光功率条件下，激光光斑半径越小，则光斑覆盖区域内激光功率密度越大，电池内部对光子的吸收率增大，对外损耗的能量越少，电池温升速率变快，温升幅度变大。而光斑区域外的温度上升主要由温差形成的热传导造成的。
当入射激光功率为0.8W时，激光光斑半径越小，电池在x方向的温度差值越大。辐照时间t=100s，激光光斑半径a=8mm时，最高温度差ΔT=1K;当激光光斑半径a=2mm时，最高温度差ΔT=8K，如图 13、图 14所示。温度上升除了对电池的转换效率产生不利影响外，温度差引起的热膨胀会产生热应力，对电池造成损伤，而且温度差越大，越容易导致电池损伤，影响电池使用寿命，因此，激光输能时激光光斑应全部覆盖电池表面，有利于提高光电池工作性能和电池寿命。
Figure 13. Temperature field distribution under laser spot radius at 8mm
Figure 14. Temperature field distribution under laser spot radius at 2mm
-
激光辐照硅光电池时的简化示意图如图 15所示。当激光束的入射角为θ时，可分解为垂直于光电池表面和平行于电池表面的两束激光，分别为垂直入射的输入功率P1和水平入射的输入功率P2，实际对光电池温度影响起有效作用的只有P1.，其有效入射功率表达式为：
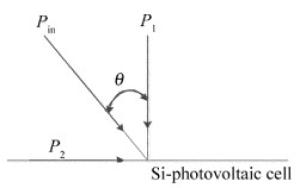
Figure 15. Schematic diagram of silicon photovoltaic cell irradiated by different laser incidence angle
$ {P_1} = {P_{{\rm{in}}}}\cos \theta = \varphi {\rm{ \mathsf{ π} }}{a^2}\cos \theta $
(13) 在忽略激光入射角对光的反射率影响时，激光入射角对光电池温度场的影响实际是通过改变入射到电池表面的激光功率密度实现的。激光入射角变化，有效的激光辐照功率密度随之改变，从而导致光电池温度场的变化。当激光入射角为0°时，有效激光功率密度最大，光电池能获得的光电池的转换效率最高。
-
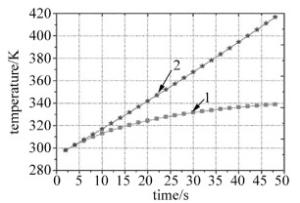
激光辐照下光电池的温度场与热辐射、热对流密切相关。当激光功率密度为2000W/m2、辐照时间为50s时，电池中心温度变化规律如图 16所示。曲线1为考虑热辐射和热对流情况下电池表面中心的温升情况; 曲线2为未考虑热辐射和热对流(绝热)情况下电池表面中心的温升情况。二者均表明, 电池中心温度随辐照时间的增加而呈上升趋势，但绝热时的温升速度要比存在热辐射和热对流时快，这是由于热辐射和热对流使电池表面的能量累积速度比绝热条件下进行得慢。因此，热辐射和热对流条件对激光辐照下光电池的温度场影响较大，增加电池表面的热辐射和热对流强度，有利于降低电池温度。
Figure 16. Temperature change curve of cell surface
-
构建了高斯激光束辐照下硅光电池的2维物理模型和热模型，用COMSOL和MATLAB软件数值模拟了连续激光辐照硅光电池的温度场分布，分析了激光辐照时间、功率密度、光斑面积、入射角以及热辐射和热对流对光电池温升的影响。
(1) 当激光功率密度为2000W/m2时，电池温度随辐照时间先快速上升，在20s后缓慢增加，100s达到热平衡后趋于一个常温值。
(2) 激光功率密度越大，电池温升速率越快，达到热平衡态时的温度值越高。而激光功率密度约为2000W/m2时，光电池的光电转换效率最高。
(3) 光斑面积近似为光电池面积时，电池表面温度差值越大。
(4) 激光入射角为0°时，有效激光辐照功率密度最大，对电池温度场影响最大。
(5) 热辐射热对流条件对电池温度场的影响较大，有利于降低电池温度。
综上所述，在本文中建立的模型基础上，从温度对光电池的光电转换效率影响角度出发，仿真分析了热源、温度与光电转换效率三者的关系，在以获得最佳光电转换效率为目标时，激光应垂直照射到光电池表面，以增大有效的入射激光功率密度，且激光光斑应全部覆盖住电池，以减小电池表面温度梯度，避免热效应影响电池的工作性能，而且入射的激光功率密度应取2000W/m2，这样才能保证电池处于最佳的工作状态，进而获得最佳的光电转换效率。
激光输能光电池温度场数值模拟
Numerical simulation of photovoltaic cell temperature field of laser power beaming
-
摘要: 温升效应是影响激光输能光电转换效率的重要原因。为了分析温升效应对光电转换效率的影响，采用基于COMSOL Multiphysics多物理场耦合软件和MATLAB软件联合仿真的数值模拟方法，建立了光电池的物理模型和热模型，得到了激光辐照时间、功率密度、光斑面积、入射角以及热辐射和热对流对温度场的影响结果。结果表明，2000W/m2激光功率密度辐照下，光电池温度随辐照时间先快速上升，20s后缓慢增加，100s达到热平衡态后温度稳定在343K；随着激光功率密度增大，电池温升速度越快，达到热平衡态时的温度值越高；激光光斑全部覆盖电池表面时，电池表面温度差值最小；入射角通过影响有效激光辐照功率密度来影响电池温升；热辐射和热对流对降低光电池温度十分有利；当激光入射角为0°、激光功率密度辐照约为2000W/m2、激光光斑面积近似为电池表面面积时，光电池能获得最佳的光电转换效率。可见对光电池温度场进行仿真分析为研究提高激光输能光电转换效率的方法提供了理论参考。Abstract: Temperature effect is an important factor affecting photoelectric efficiency of laser power beaming. To analyze the impact of temperature effect on photoelectric efficiency, physical model and thermal model of photovoltaic cells were established based on numerical simulation combing COMSOL Multiphysics software and MATLAB software. The effects of irradiation time, power density, beam size, incident angle, thermal radiation and heat convection on temperature field were obtained. The results show that under power density of 2000W/m2, photovoltaic cell temperature rises rapidly at the first, increases slowly after 20s and tends to the constant value of 343K after 100s with thermal equilibrium. The greater the power density, the faster the cell temperature, the higher the temperature which reaches thermal equilibrium time. When the cell surface is covered by laser spot completely, the temperature difference on the surface is minimum. The influence of incident angle on temperature rise of cell is affected by the effective laser power density. Heat radiation and heat convection are very favorable for decreasing cell temperature. When laser incident angle is 0°, laser power density is about 2000W/m2, and laser spot area is approximately cell surface area, the photovoltaic cell can obtain the best photoelectric efficiency. The study provides theoretical reference for improving photoelectric efficiency.
-
Key words:
- laser technique /
- laser power beaming /
- numerical simulation /
- temperature field /
- photovoltaic cell
-
Figure 6. Relationship between photoelectric efficiency and temperature under different laser power densities
Figure 7. Relationship between photoelectric efficiency and laser power density under different temperature
Figure 9. Relationship between temperature of the center point and the irradiation time
Figure 10. Relationship between temperature at center point and time under different power density
Figure 11. Relationship between temperature and time under different laser spot radius under the same φ
Figure 12. Temperature field distribution under different laser spot radius under the same Pin
Figure 15. Schematic diagram of silicon photovoltaic cell irradiated by different laser incidence angle
Table 1. Efficiency parameters of photoelectric conversion
parameter value of expression the Boltzmann constant k 1.3806505×10-23J·K-1 unit charge e 1.6022×10-19C diode ideal factor n 2 internal quantum efficiency at room temperature E(T0) 0.95 internal quantum temperature coefficient kT 8×10-4 reverse saturation current at room temperature Ir 8×10-6A laser spot radius a 102mm laser wavelength λ 980nm laser power density φ 2000W·m-2 parallel resistance Rsh 106Ω series resistance Rs 0.1Ω band gap Eg 1.13eV reflectivity R 0.1 
下载: 导出CSV
Table 2. Thermal physical property of silicon photovoltaic cells
parameter value of expression thermal conductively κ 150W·m-1·K-1 density ρ 2400K·m-3 specific heat capacity c 700J·kg-1·K-1 surface coefficient of heat transfer h 5W·m-2·K-1 thermal radiation rate εf 0.95 thermal radiation rate εb 0.9 absorption coefficient α 0.9 initial temperature T0 298K
下载: 导出CSV
-
[1] LI Zh Y, ZHANG J D, HUANG X J. Laser wireless power transmission technology for solar power satellite[J]. Spacecraft Engineering, 2015, 24(1):31-37(in Chinese). [2] SHEN J Sh, CHENG K, MA B, et al. Application method of laser power transmission in orbit[J]. Spacecraft Engineering, 2015, 24(1):25-30(in Chinese). [3] LI Y, ZHANG Q, ZHANG C. Research on laser wireless energy transmission technology for UAV[J]. Winged Missiles Journal, 2015(1):58-61(in Chinese). [4] WU G Sh, WEN T, WANG Zh W, et al. Study on temperature characteristics of solar cells[J]. Telecon Power Technologies, 2013, 30(1): 19-22(in Chinese). [5] SIDDIQUI M U, ARIF A F M, KELLEY L, et al. Three-dimensional thermal modeling of a photovoltaic module under varying conditions[J]. Solar Energy, 2012, 86(9):2620-2631. doi: 10.1016/j.solener.2012.05.034 [6] ZHOU J, YI Q, WANG Y, et al. Temperature distribution of photovoltaic module based on finite element simulation[J]. Solar Energy, 2015, 111(6):97-103. [7] LI J, SUN W J, SUN J N, et al. Numerical analysis of CW laser damage in GaAs[J]. Acta Photonica Sinica, 2012, 41(5):571-574(in Chinese). [8] ZHOU H J, SUN W J, LIU Zh Y. Research of nonlinear absorption effect of pulse laser irradiation for GaAs[J]. Acta Photonica Sinica, 2014, 43(11):21-25(in Chinese). [9] ZHAO F Y, ZHENG J, WANG Ch. Temperature field of semiconductor materials irradiated by CW laser[J]. Journal of Changchun University, 2011, 21(6):73-76(in Chinese). [10] YUAN Zh, HE L L. The basic characteristics of solar cells[J]. Modern Electronics Technique, 2007, 30(16):163-165(in Chinese). [11] WEI Z, JIN G, TAN Y, et al. Numerical simulation of temperature field and thermal stress field in silicon-based positive-intrinsic-negative photodiode irradiated by multipulsed millisecond laser[C]//Applied Optics and Photonics China. Washington DC, USA: SPIE, 2015: 1-7. [12] CHIN V J, SALAM Z, ISHAQUE K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review[J]. Applied Energy, 2015, 154(1):500-519. [13] LANDIS G A. Photovoltaic receivers for laser beamed power in space[J]. Journal of Propulsion & Power, 1993, 9(1):1494-1502. [14] JIANG H M, CHENG X A, LI W Y. Response of silicon p-n junction solar cell to DF laser irradiation[J]. High Power Laser Particle Beams, 2003, 15(1):21-24(in Chinese). [15] DURGADEVI A, ARULSELVI S, NATARAJAN S P. Photovoltaic modeling and its characteristics[C]//Emerging Trends in Electrical and Computer Technology. New York, USA: IEEE, 2011: 469-475. [16] LIU X. Dynamic thermal model of photovoltaic cell illuminated by laser beam[C]//Pacific Rim Laser Damage.Washington DC, USA: SPIE, 2015: 1-8. [17] RADZIEMSKA E. Thermal performance of Si and GaAs based solar cells and modules: a review[J]. Progress in Energy & Combustion Science, 2003, 29(5):407-424. [18] QIU D D, WANG R, CHENG X A, et al.Wave band effect of solar cells under irradiation of CW laser[J]. Laser Technology, 2011, 35(5):632-635(in Chinese). -
点击查看大图
图(16) / 表(2)
计量
- 文章访问数: 3557
- HTML全文浏览量: 2171
- PDF下载量: 246
- 被引次数: 0
