大型航天器结构复杂、功能众多，其在轨检修、维护一直是航天界的焦点问题，是进一步提高大型航天器的可靠性与安全性的关键^[1]。“哥伦比亚”号航天飞机在归途中解体，事后分析表明，失事原因之一是覆盖在航天飞机外层的一片隔热瓦脱离引起飞机外表融化解体。因此，对于大型航天器表面结构的在轨检测是保障航天器在轨正常运行的有效途径之一^[2]。但是有航天员参与的在轨检测面临诸多困难；空间机械臂曾被应用于航天飞机的隔热瓦损伤在轨检测，具备精确操作能力和视觉识别能力，而空间机械臂也存在作用范围有限，不能全方位地对航天器进行观察和监视的不足^[3]。因此，空间自由飞行机器人在轨服务中具有明显优势。美国国家航空航天局(National Aeronautics and Space Administration，NASA)约翰逊空间中心的工程师设计开发了一颗可以在航天器外自由飞行的微小航天器(miniature autonomous extravehicular robotic camera, Mini AERCam)，旨在帮助宇航员及地面成员在任务执行期间观察航天器外部情况。该Mini AERCam采用的是惯性/全球定位系统(global positioning system，GPS)导航系统进行导航，但是精度有限，并且不适合在没有全球卫星导航系统(global navigation satellite system，GNSS)信号的高轨使用。

区别于AERCam使用差分GPS，本文中提出利用线激光三角测量装置提取目标航天器表面结构点云信息^[4-5]，并与已知的外形结构数据匹配来获取两者之间的相对位姿关系^[6]。其中线激光三角测量装置中的结构参量需要精确标定，才能实现精确可靠的测量。

对于激光三角测量系统，常见的标定方法有拉丝法、锯齿靶法、微分法、已知直线与图像点匹配法、基于3维靶标法和本文中采用的基于自由移动标定物的激光测量标定方法^[7-11]。这些方法在标定过程中都需要测量激光器端口与标定物间的距离作为系统的标定输入，但是激光器端口的位置无法准确确定，所以这个距离的测量值存在较大的误差^[12]。为了提高测量系统的精度，本文中提出了基于距离差的标定方法，建立了基于距离差的标定模型，回避了绝对距离的测量，利用容易获取的标定物的移动距离作为标定输入，标定过程实施简单、精度较高。

本文中的激光三角测量系统，测量距离在1m左右，测距精度为4.000mm。激光三角测量法作为一种传统的激光测距方法，有着结构简单、测量频率高、数据可实时更新、体积小、质量轻的优点^[13-15]。在实验中使用的基于距离差的标定方法有效提高了激光三角测量的精度，测距范围及实时性均满足本文中的要求。

在标定物表面上，用一束激光以一定的角度照射，激光在标定物表面发生反射，在另一个角度用成像系统对激光反射光进行汇聚成像。由于入射和反射光构成一个三角形，如果标定物沿着激光束的方向发生位移时，则相机成像平面上的像点也会发生相应位移，通过物像位移之间的关系可以计算出被测物面各点的坐标。

按入射激光光束与被测物面的角度不同，可以把激光三角测量法分为斜射式和直射式两种。斜入射和直入射都可以实现对标定物进行非接触测量。一方面，直入射较斜入射式体积更小，光强集中，光斑变形小；另一方面，直入射式与斜入射式的测量模型在本质上是一致的，所以采用直入射法进行标定方法的研究。

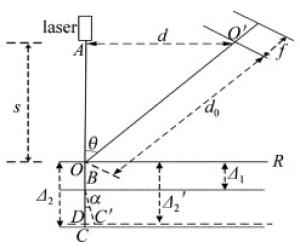
垂直激光三角测量原理如图 1所示。图中，s为激光器光束端面A与基准面R的垂直距离，d为端面A与相机焦点O′的距离，d₀是OO′的距离，f是相机焦距，可以使用基于2-D平面靶标的摄像机标定方法标定得到，Δ为被测物体距离基准面的距离，θ是激光束与OO′的夹角，δ是在成像平面上成像点偏移的距离，可以求得公式：

Figure 1.  Vertical laser triangulation measurement

式中，虽然OO′的长度d₀、镜头的焦距f、激光束与镜头的夹角θ均为定值，在测量时是固定不变的，但是在测距系统装配时很难获得其准确值。因此，为了让激光三角测量系统精确地测量位移，在激光三角测量系统装配完毕后需要对这些参量进行精密标定。

如图 1所示，由于激光器发出激光束端面A无法准确判定，所以在标定时端面A与被测物体的距离无法直接测得。本文中提出了一种根据距离差进行标定的新方法，根据(1)式得到如下公式：

式中，i和(i+1)为两次标定物移动的次数，δ_i, δ_i+1为像点在成像平面上的横坐标，可以通过对所拍图像的处理得到，Δ_i+1－Δ_i为任意两次标定物移动的距离，可以直接通过测量得到。令a=f sinθ/d₀，b=cosθ/d₀，y=Δ_i+1－Δ_i，x_i+1=1/δ_i+1，x_i=1/δ_i，得到公式：

由于Δ_i+1－Δ_i与δ_i，δ_i+1的值之间是非线性关系，本文中利用非线性回归分析的方法来求a，b的值，并由公式θ=arctan(af^-1b^－1)和d₀=b^-1cosθ计算得到θ和d₀的值，从而完成激光三角测量系统的准确标定。

本文中采用高斯-牛顿迭代法来计算a，b的估计值。首先，选取a₀，b₀作为a，b的初始估计值，将(3)式在点(a₀, b₀)处展开成泰勒级数，并忽略2阶以上的高阶项，得到如下方程：

式中，da, db为参量a, b的微分量，$\mathit{\hat y}$为函数y泰勒展开式的第1项，m和n为函数y泰勒展开式1阶项的系数；其中：

根据(4)式给出标定公式的矩阵描述：

式中，ε为误差项矩阵，(6)式可使用加权最小二乘法进行计算，当计算出X后，执行a_i+1=a_i+da，b_i+1=b_i+db，可迭代固定次数或者改正量小于某一阈值, 即可迭代计算，直到第n次计算得到比较理想的参量估计值a_n和b_n，并以此次的计算值作为a和b的标定值。

本文中的测量系统使用的是线激光光源，线激光光源照射到被测物面的光带是有一定宽度的，因而它在相机上的成像并不是一个像素的宽度，激光束在成像平面上的成像宽度是占用几个像素甚至几十个像素，如图 2所示。所以在图像处理的过程中就涉及到激光线中心点提取的问题。

Figure 2.  Relationship between gray value and cross section width

一般认为，激光光带的灰度分布是成高斯对称分布的。但由于受到外界环境和传感器内部噪声影响，接收的光斑波形发生改变。根据这个特性，本文中采用重心法求激光带中心点坐标^[2]。首先，确定一个光带边界的灰度阈值T，然后在图像的每一行上判断出灰度值大于T的像素，利用重心公式计算光心的位置。假设在图像的一行上，灰度值大于阈值T的像素点坐标为u_j，其灰度值为g_j，其中，j=1, 2, 3, …, M(M为大于阈值T的像素的个数)。利用重心公式可以得到光心的位置u为：

利用这种方法得到的光带中心是亚像素级的，该算法在图像背景较暗的情况下具有很好的效果。

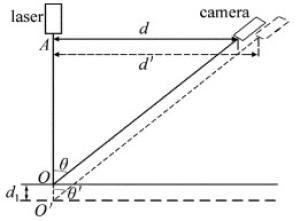
测量系统标定过程中，标定物移动的方向与激光束的方向不会完全一致，如图 3所示。当标定物移动方向与激光束方向夹角为α时，移动距离BC′=BC，有效移动距离为BD，其长度小于BC′，使得标定物的实际移动距离Δ₂′-Δ₁小于标定计算中使用的移动距离Δ₂－Δ₁，从而产生误差。本文中将标定物移动方向与激光束方向之间的误差角α导致的标定误差称为非垂直误差。

Figure 3.  The diagram of the moving direction of calibration object

令标定物移动的距离为l，则标定物移动方向与激光束方向夹角α和标定距离误差e的关系如下所示：

对非垂直误差的分析在第2节中详细分析说明。

首先搭建激光三角测量系统的实验装置，本文中研究的测量系统硬件系统包括：线激光器、红外滤镜、标定物和相机。激光器和相机固定在工作台上，如图 4所示。

Figure 4.  Experimental device of laser triangulation distance measurement

本系统需要采集多组相对深度数据，取一个标定模板放置于线激光器正前方，使标定物与激光束的方向垂直，沿激光束方向多次移动标定物，移动距离分别为30.000mm, 50.000mm, 100.000mm, 150.000mm, 200.000mm, 250.000mm, 300.000mm, 350.000mm, 400.000mm, 450.000mm，共移动10次。随着标定物移动距离的增加，激光束在相机成像平面上的成像位置在不断移动，如图 5所示。

Figure 5.  Moving process of laser line on camera imaging plane

相机的焦距经标定得到f=15.332mm，利用第1.2节中的原理处理所拍图像，得到a=0.00520, b=0.00159，由此计算可得测量系统的参量θ=12.041°, d=128.316mm，激光器与基准面距离s=601.560mm。

同样采用距离差的方法来验证标定的准确性，重新在实验中每隔50.000mm移动一次标定物并采集一组图像。通过分析图像得到的参量δ和标定实验中计算得到的测量系统的参量，利用(1)式计算得到激光束端口与标定物距离，从而检验这些参量是否准确，见表 1。

从表 1中的数据可以看出，在400.000mm~900.000mm的范围内测距，实验中由非垂直误差以及实验仪器本身的精度等一系列因素引起的误差优于4.000mm，满足要求。上述实验数据表明，本文中提出的实验标定方法的测量精度能够达到毫米级。

如果采用未改进的测量系统的标定方法，直接测量激光器端口与标定物的距离，假定激光器端口与标定物的距离测量时误差为比实际距离减少5.000mm，利用前面计算得到的激光器与基准面距离为已知值，通过第1.2节中的原理处理所拍图像, 并采用最小二乘法对(1)式进行计算的得到测量系统的参量θ=10.725°，d=101.075mm，激光器与基准面距离s=533.648mm。

采用前面改进方法中验证标定的准确性所采集的数据进行复核计算。利用(1)式计算得到激光束端口与标定物距离，与改进方法中复核计算的标定距离作比较，从而检验这些参量是否准确，如表 2所示。

从表中的数据可以看出，由于测量激光器端口与标定物的距离减少了5.000mm，最终标定出来的测量系统的测量误差很大, 其测量出的移动距离精度也略低于改进方法的精度; 同时, 与改进后的测量方法测量标定物的实际距离相差了50.000mm以上，而改进后的测量系统测量标定物的距离经测量验证与实际距离误差很小，所以未改进的方法测量出的距离误差比较大。上述实验数据表明，本文中提出的实验标定方法的测量精度比与未改进的测量方法准确了很多。

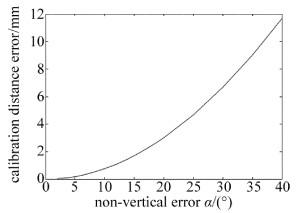
第1.3节中已经分析了当标定物移动方向与激光束方向存在误差角α时，标称移动距离比实际移动距离要大。

假设每次标定物移动的距离l=50.000mm，随着α的增加，标定距离误差如图 6所示。

Figure 6.  Relationship between calibration distance error and α

由图 6可以看出，标定距离误差与α大小呈非线性变化。同时开展仿真研究，探索非垂直误差对最终测量结果的影响规律。令相机参量为f=15.000mm，三角测量系统参量θ=12.000°, d=120.000mm，激光器与基准面距离设定为s=564.560mm。假设α=5.000°时，初始标定物距离为450.000mm时，每隔50.000mm采集一次图像，即实际标定的距离为450.000mm, 499.809mm, 549.619mm, 599.429mm, 649.239mm, 699.049mm, 748.859mm, 798.669mm, 848.479mm, 898.289mm，经标定后得到的三角测量系统的参量为θ=12.0001°，d=120.46mm，激光器与基准面距离s=566.718mm。

图 7为含有非垂直误差的激光三角测量系统。利用含有非垂直误差的标定参量进行测量计算，结果与实际距离的比较如表 3所示。

Figure 7.  Laser triangulation measurement with non-vertical error

由此可见，当激光三角测量系统存在非垂直误差时，每次测量距离的间隔变为50.191mm，随着测量距离的增加，测量距离与实际的误差也在增加。这是由于在标定的时候，存在非垂直误差，使得计算中将每次标定物的实际移动距离49.809mm作为50.000mm进行计算，从而使得到的激光三角测量系统测量的距离比实际距离要大。在测量时，标定物移动距离50.000mm，测量得到的距离间隔为50.191mm，即测量得到的距离间隔比实际距离间隔要大。

本文中提出了利用距离差对激光三角测量系统进行标定的方法，解决了三角测量法在标定时，无法直接准确地测量激光器与标定物距离的问题。同时，作者通过仿真对激光像点的提取误差和非垂直误差进行了分析。实验结果表明，该方法结构简单并能够准确地对激光三角测量系统进行标定，系统精度可以达到4.000mm，为基于惯性/激光三角测量的航天器相对导航的研究提供了基础。