网站地图
下载:
-
偏光分束棱镜可以将一束自然光分成振动方向相互垂直的两束线偏振光[1]，因此在现代激光和偏光技术中有着非常重要的应用[2-4]。偏光分束棱镜的种类很多，如渥拉斯顿棱镜[5-8]、双渥拉斯顿棱镜[9-10]、洛匈棱镜和可调分束角棱镜[11]等，对于这些分束棱镜的分束特性在国内外已有研究[12-13]，SIMON等人[14]对渥拉斯顿棱镜进行了改进设计，得到分束角大的偏光棱镜，且给出了分束角与入射角的关系。LI等人[15-16]设计了可调分束角棱镜，并对其分束角特性进行了研究。WANG和HUANG等人[17-18]在双渥拉斯顿棱镜的基础上，通过改变棱镜光轴或结构角，获得分束角对称输出的效果。在激光显微技术和光纤耦合系统以及光隔离器等应用中，常用到分束角较小的偏光分束器件，微角分束偏光棱镜在其中起到重要的作用；另外，由于微角分束偏光棱镜是单元晶体结构，因此适合于对高功率激光束的偏振分束。到目前为止，对于微角分束偏光棱镜分束性能的研究还少见报道，为此，本文中以冰洲石晶体微角分束偏光棱镜为例，研究入射光的波长和入射光的入射角对分束角的影响及其规律，为微角分束偏光棱镜的实际应用提供分束角特性的参考。
-
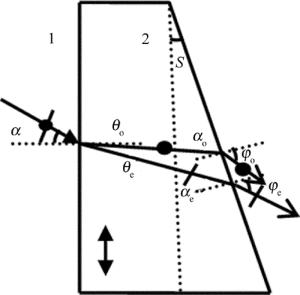
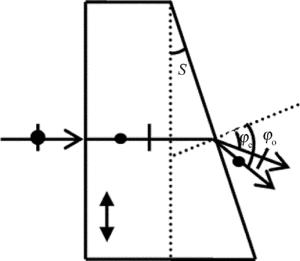
微角分束偏光棱镜属单元式结构，棱镜的结构和分光光路如图 1所示。图中双箭头表示晶体光轴方向，S表示棱镜的结构角。在本文的分析中，对涉及与光有关的角度作如下约定：由光线(或光波)到介面法线顺时针所成的角为正，逆时针所成的角为负。
Figure 1. Prism structure and beam path
-
当一束非偏振光正入射于棱镜时(见图 1)，由于进入棱镜的光传播方向与晶体光轴垂直，则寻常光(o光)和非寻常光(e光)传播方向相同，但是传播的速度不同。由于o光、e光波主折射率的不同，在棱镜的出射界面，o光、e光的折射角也不同，分束角φ的大小即为两束光折射角的差值。φo和φe分别表示o光和e光在出射介面的折射角的大小，由折射定律和图 1中的几何关系可以得到：
$ \left\{ \begin{array}{l} {\varphi _{\rm{o}}} = \arcsin ({n_{\rm{o}}}\sin S)\\ {\varphi _{\rm{e}}} = \arcsin ({n_{\rm{e}}}\sin S) \end{array} \right. $
(1) 则分束角的大小为：
$ \varphi = \arcsin ({n_{\rm{o}}}\sin S) - \arcsin ({n_{\rm{e}}}\sin S) $
(2) 式中, no和ne是棱镜中冰洲石晶体的主折射率，它们色散关系由下两式给出[19]：
$ {n_{\rm{o}}}^2 = 2.6926 + \frac{{0.0192}}{{{\lambda ^2} - 0.0195}} - 0.0143{\lambda ^2} $
(3) $ {n_{\rm{e}}}^2 = 2.1846 + \frac{{0.0085}}{{{\lambda ^2} - 0.0143}} - 0.0023{\lambda ^2} $
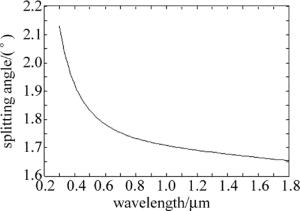
(4) 图 2是当S=0.175rad时，由(2)式~(4)式拟合的棱镜分束角与工作波长的关系曲线。由图中曲线可以看出：对于确定的棱镜结构角，微角分束偏光棱镜的分束角随工作波长的增大而变小。
Figure 2. Relationship between splitting angle and wavelength when S=0.175rad
-
当光以一定的角度α入射时，棱镜的分光光路如图 3所示。由于晶体中o光、e光对应的折射率不同，入射光经介面1的折射，棱镜中的o光、e光波折射角也不同，从而o光和e光发生分离，其在介面1上的折射角分别为θo和θe，在介面2上入射角分别为αo和αe，折射角分别为φo和φe。
Figure 3. Beam path of non-normal incidence
对于o光，在介面1和介面2上折射分别为：
$ \sin \alpha = {n_{\rm{o}}}\sin {\theta _{\rm{o}}} $
(5) $ {n_{\rm{o}}}\sin {\alpha _{\rm{o}}} = \sin {\varphi _{\rm{o}}} $
(6) 由以上两式及图 2中的角度关系αo=S+θo，可得介面2上o光的折射角为：
$ {\varphi _{\rm{o}}} = \arcsin \left\{ {{n_{\rm{o}}}\sin \left[ {S + \arcsin \left( {\frac{{\sin \alpha }}{{{n_{\rm{o}}}}}} \right)} \right]} \right\} $
(7) 对于e光，同样有：
$ \sin \alpha = {n_{\rm{e}}}^\prime \sin {\theta _{\rm{e}}} $
(8) $ {n_{\rm{e}}}^\prime \sin {\alpha _{\rm{e}}} = \sin {\varphi _{\rm{e}}} $
(9) αe=S+θe，e光在第2个面上的折射角为:
$ {\varphi _{\rm{e}}} = \arcsin \left[ {{n_{\rm{e}}}^\prime \sin(S + {\theta _{\rm{e}}})} \right] $
(10) 于是得到微角分束偏光棱镜的分束角关于入射角的关系式为：
$ \begin{array}{l} \varphi = {\varphi _{\rm{o}}} - {\varphi _{\rm{e}}} = \arcsin \left\{ {{n_{\rm{o}}}\sin \left[ {S + \arcsin \left( {\frac{{\sin \alpha }}{{{n_{\rm{o}}}}}} \right)} \right]} \right\} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\arcsin \left[ {{n_{\rm{e}}}^\prime \sin(S + {\theta _{\rm{e}}})} \right] \end{array} $
(11) 式中,
$ {n_{\rm{e}}}^\prime = \frac{{{n_{\rm{o}}}{n_{\rm{e}}}}}{{{{({n_{\rm{o}}}^2{{\cos }^2}{\theta _{\rm{e}}} + {n_{\rm{e}}}^2{{\sin }^2}{\theta _{\rm{e}}})}^{\frac{1}{2}}}}} $
(12) $ {\theta _{\rm{e}}} = \arctan \left[ {\frac{{{n_{\rm{o}}}\sin \alpha }}{{{{({n_{\rm{e}}}^2{n_{\rm{o}}}^2 - {n_{\rm{e}}}^2{{\sin }^2}\alpha )}^{\frac{1}{2}}}}}} \right] $
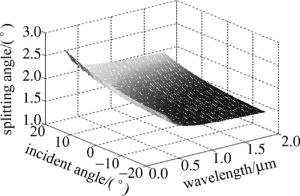
(13) 以冰洲石晶体为双折射材料，取微角分束偏光棱镜的结构角S=0.175rad，由(2)式~(4)式和(11)式~(13)式, 通过MATLAB软件模拟的分束角与工作波长和入射角的关系, 如图 4所示。
Figure 4. Relationship of splitting angle, incident angle and wavelength
-
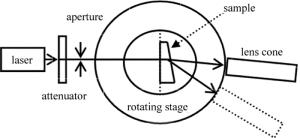
对微角分束偏光棱镜样品分束角的测量是在精度为0.5″的测角仪上进行的，实验装置与光路如图 5所示。首先，调节激光器使光点在观测镜筒的十字叉丝的中心处；然后把待测棱镜的前端面置于载物台的中线上；调节棱镜，使入射面的反射光至光阑的中心位置，以此调整光的垂直入射；通过旋转载物台，即可调节光在样品上的入射角度。
Figure 5. Experimental installation and beam path
-
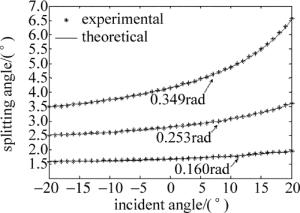
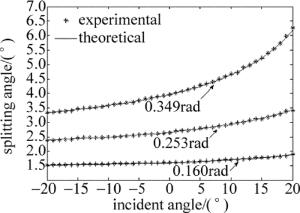
3只待测微角分束偏光棱镜样品的结构角分别为0.160rad, 0.253rad和0.349rad。用473nm, 633nm和670nm 3种不同波长的激光，在光正入射的情况下，分别对3只样品棱镜的分束角进行了测量，测试数据如图 6所示。作为比较，利用MATLAB软件，拟合出了3只样品棱镜分束角与工作波长的关系曲线(见图 6)，由图可见：(1)实验测试的分束角均在理论拟合曲线上，由此证实了给出的理论分析是正确的；(2)当棱镜用于复色光时，由于光束中每一个波长对应的分束角不同，会导致出射的两偏振光束的发散角变大。
Figure 6. Relationship between splitting angle and wavelength
-
同样采用图 5的测量光路, 用473nm, 633nm和670nm 3个波长的光源, 通过旋转载物台改变入射角度，在-20°~20°之间，每隔1°测量一次，对3只样品棱镜的分束角进行了测量，测量数据如图 7~图 9所示，图中实线为拟合的理论曲线。由图可见：(1)测试数据与理论曲线吻合得很好; (2)当光在棱镜上的入射角由-20°~20°连续变化时，微角分束偏光棱镜的分束角由小到大连续变化，且波长越短变化越大，棱镜结构角越大变化越大。这种变化提示，在棱镜的使用中，可以通过光束在棱镜上的入射角，得到所需要的分束角。
Figure 7. Relationship between splitting angle and incident angle at 473nm
Figure 8. Relationship between splitting angle and incident angle at 633nm
Figure 9. Relationship between splitting angle and incident angleat at 670nm
-
冰洲石晶体是制作偏光分束棱镜的主要双折射材料，本文中依据冰洲石晶体的光学性质，从原理上推导出了微角分束偏光棱镜的分束角随工作波长和入射角的变化关系式，通过MATLAB软件模拟出了分束角与工作波长和入射角的关系及规律，即对于结构角一定的微角分束偏光棱镜，其在短波长的分束角大于长波长；当入射角为负时，随着入射角的增大，分束角变小，而入射角为正时，分束角随入射角的增大而变大。对制作的3个不同结构角的棱镜样品进行了实验测试，测试结果与理论分析相吻合。由此可见：(1)当微角分束偏光棱镜用于宽光谱时，需要注意分束角光谱分布的影响；(2)可以通过改变入射角获得所需要的棱镜分束角。
本文中的分析与实验测试均是针对冰洲石晶体制作的微角分束偏光棱镜进行的，对于结构角一定的棱镜，由于其分束角与工作波长的关系取决于材料双折射率的色散，那么只要双折射率(与冰洲石晶体相同)属于正常色散的单轴晶体，如钒酸钇晶体制作的微角分束偏光棱镜，其在短波长的分束角同样大于长波长。在分束角与入射角的关系方面，由于钒酸钇晶体是正单轴晶体，非寻常光在出射介面上的折射角要大于寻常光的折射角，这是与冰洲石晶体是不同的，但通过分析两种晶体制作的棱镜分束角随入射角的变化规律发现，其结果是一致的。
微角分束偏光棱镜分束角的特性研究
Characteristics of splitting angles of micro-angle beam splitting polarization prisms
-
摘要: 为了了解微角分束偏光棱镜的分束特性，根据冰洲石晶体的光学性质以及光在棱镜入射与出射介面和棱镜中的传播方向，在光正入射的条件下，分析了棱镜的分束角随工作波长的变化关系; 在工作波长一定的条件下，分析了入射角对棱镜分束角大小的影响及规律; 设计了实验，对制作的棱镜样品进行了实验测试。结果表明，微角分束偏光棱镜的分束角随工作波长而变，且波长越短，分束角越大; 在棱镜的主截面内，入射角由-20°~20°变化时，分束角呈非线性由小变大。这一结果对于微角分束偏光棱镜的设计和使用具有实际价值。Abstract: In order to study splitting characteristics of micro-angle beam splitting polarization prisms, according to optical properties of calcite crystals, from propagation direction of the light in incident interface, exit interface, and prism internal, the relationship between splitting angle and wavelength was analyzed at normal incidence. For a certain wavelength, the influence of incident angle on beam splitting angle was analyzed. After the experiment of three prism samples, the results show that splitting angle of a micro-angle beam splitting polarization prism changes with the change of wavelength of the incident light. The shorter the wavelength, the greater the splitting angle. In the principal cross section of prism, the change range of incident angle is of -20°~20° and splitting angle increases nonlinearly. The results have certain value for the design and usage of micro-angle beam splitting polarization prisms.
-
Key words:
- polarization optics /
- polarization beam /
- splitting angle /
- incident angle /
- operating wavelength
-
[1] LI J Zh. Handbook of optics[M].Xi'an: Shaanxi Science and Technology Press, 1986:483-531(in Chinese). [2] ZHANG C M, LIU N, WU F Q. Analysis and calculation of Glan-Taylor prism's transmittance at full angle of view in a polarization interference [J].Acta Physica Sinica, 2010, 59(2):949-956(in Chinese). [3] SOREF R A, MCMAHON D H. Optical design of Wollaston-prism digital light deflectors[J].Applied Optics, 1966, 5(3):425-434. doi: 10.1364/AO.5.000425 [4] ZHOU J, SU G Y, SHI R Y. The influence of adjustable beam splitting prism on laser beam[J]. Laser Technology, 2002, 26(1):75-78(in Chinese). [5] ZHU J K, WU F Q, REN Sh F. Forward and backward splitting angles of Wollaston prisms and their symmetry[J]. Laser Technology, 2012, 36(5):636-638(in Chinese). [6] ZHU H F, SONG L K, WU F Q. et al. Calculation of the splitting angle of Wollaston prism by means of coordinate conversion[J]. Laser Technology, 2003, 27(4):362-364(in Chinese). [7] WONG G, PILKINGTON R, HARVEY A R. Achromatization of Wollaston polarizing beam splitters [J].Optics Letters, 2011, 36(8):1332-1334. doi: 10.1364/OL.36.001332 [8] DENG H Y, WU F Q, TANG H J. The spectral properties of the splitting angle for Wollaston prism[J]. Laser Journal, 2005, 26(4):42-43(in Chinese). [9] ZHU H F, NAN Y J, YUN M J, et al. Precise analysis of the intensity splitting ratio of double Wollaston prism[J]. Acta Optica Sinica, 2012, 32(6):0623002(in Chinese). doi: 10.3788/AOS [10] WANG W, WU F Q, SU F F. A modified symmetric splitting angle prism[J]. Journal of Optoelectronics·Laser, 2003, 14(9):913-916(in Chinese). [11] ZHU H F, SONG L K, WANG X M. Study about splitting intensity ratio of a prism with variable beam splitting angle[J]. Optical Technique, 2003, 29(5):614-616(in Chinese). [12] MA L L, SONG L K, WU F Q, et al. Splitting angle and light intensity splitting ratio of single-element polarized beam splitting prisms[J]. Laser Technology, 2008, 32(3):299-301(in Chinese). [13] WANG C M, SONG L K, WANG L, et al. Effect of incident angles on splitting ratio of Glan polarizing splitting prisms[J]. Laser Technology, 2008, 32(2):212-214(in Chinese). [14] SIMON M C. Wollaston prism with large split angle[J]. Applied Optics, 1986, 25(3):369-376. doi: 10.1364/AO.25.000369 [15] LI G H. Adjustable beam splitting prism[J]. Journal of Optoelectronics·Laser, 1982, 2(1):60-64(in Chinese). [16] LI G H, WU F Q, YU D H. The dependence of beam splitting angle of adjustable beam splitting prism on the incident angle[J]. Journal of Qufu Normal University, 1991, 17(2):54-57(in Chinese). [17] WANG W, WU F Q, SU F F. Symmetric polarization beam splitting prism based on three-element Wollaston prism[J]. Optical Technique, 2004, 30(2):182-186(in Chinese). [18] HUANG J Y, WU F Q, LI G H. Symmetry of beam splitting angle for uniaxial crystal prism[J]. Laser Technology, 1996, 20(2):104-107(in Chinese). [19] CHEN X Y, SHAN M. Dispersion formula of calcite[J]. Opto-Electronic Engineering, 2007, 34(5):38-42(in Chinese). -
点击查看大图
图(9)
计量
- 文章访问数: 7348
- HTML全文浏览量: 5276
- PDF下载量: 17
- 被引次数: 0
