网站地图
下载:
-
随着光通信和传感技术的快速发展, 光纤作为信号产生、采集的载体在越来越多的领域得到了广泛应用。由此产生的大量非平稳时变信号对传统的基于傅里叶变换的频谱分析和基于时域统计的分析方法提出了挑战。傅里叶频谱分析和时域统计是基于把信号看成短时平稳来处理的, 反映的是信号在一小段时间内的统计均值[1], 因而很难直观、准确地反映非平稳信号的时变特征[2]。目前光纤安防应用中采用较多的有基于频谱分析的特定频段能量、信息熵, 基于时域统计的过零率、峰均比、短时能量、相关系数等参量来反映信号特征, 但是这些算法都是将一段时间内的数据作为整体进行处理, 丢掉了随时间变化的状态信息。在实用过程中难免出现某些特征参量相差无几而波形变化迥然相异的状况, 影响系统最终判决。而近年来兴起的时频分析方法[3]——希尔伯特-黄变换(Hilbert-Huang tranform, HHT)在地震分析、机械故障诊断、语音识别、医学研究等领域的应用都获得了成功。该方法是由美籍华裔科学家HUANG等人在对瞬时频率进行深入研究后提出, 从信号自身出发采用一种叫做经验模态分解(empirical mode decomposition, EMD)的方法将原始信号分解为若干个本征模态函数(instrinsic mode function, IMF)和一个残余项的和[4]; 然后再对得到的所有IMF进行希尔伯特谱分析(Hilbert spectrum analysis, HSA)。这种方法对数据的利用率较高, 最终得到信号频率随时间变化的时频谱, 能够较全面地反映信号变化特征, 因此, 作者采用该方法对光纤振动产生的非平稳时变信号进行分析。
-
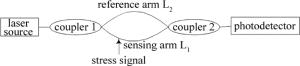
本文中的数据信号来源于实际分布式光纤安防系统。该系统采用的是马赫-曾德尔干涉结构, 如图 1所示。激光器输出的激光通过3dB耦合器1分为功率相等的两束, 分别进入马赫-曾德尔干涉结构的两臂, 经过一段距离传输后再通过一个3dB耦合器2进行干涉, 干涉光强被光电探测器检测处理后成为待分析的信号。
Figure 1. The distributed optical fiber sensor based on Mach-Zehnder structure
待分析信号之所以能够携带光纤受到的扰动信息, 是因为上述马赫-曾德尔干涉结构的两臂采用了不同的处理, 参考臂L2使用的是应力不敏感光纤, 而传感臂L1则采用了应力敏感光纤。在应力信号作用下L1中光信号会由于光纤的纵向应变、横向应变以及光弹效应的影响[5-6]而产生一个附加相位Δφ, 由于L2对应力不敏感, 所以在应力作用下光信号相位不会改变。探测器接收到的干涉光强可表示为[7]:
$ I = {I_1} + {I_2} + 2\sqrt {{I_1}{I_2}} \cos \left( {\Delta \varphi + \Delta \psi } \right) $
(1) 式中, I1和I2分别代表L1和L2中的光强, Δψ是由系统制作工艺等因素引入的初始相位差, 系统参量确定后不会再改变。因此, 对信号分析的主要工作落在了如何通过最终的强度信号来反演由应力导致的附加相位变化上。
-
希尔伯特-黄变换(HHT)中希尔伯特变换是基础, 由HUANG提出的EMD方法是核心。通过EMD得到的所有IMF有两个共同的特征:(1)过零点和极值点个数相同或相差为1;(2)通过极大值点拟合得到的上包络曲线和由极小值得到的下包络曲线的局部均值等于0[8-11]。
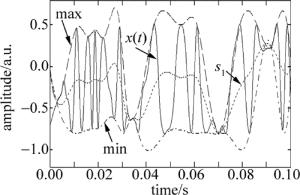
采用希尔伯特-黄变换处理信号的基本步骤是:首先利用EMD方法对信号进行分解, 得到信号的IMF表示, 然后对每一个IMF进行希尔伯特变换。下面以光纤振动信号为例简要介绍EMD方法的实现流程, 如图 2所示。首先确定出待分析信号x(t)(即本文中的光纤振动信号)的所有极值点, 然后由极大值点和极小值点分别可确定一条拟合曲线(即max和min曲线), 作为x(t)的上下包络线。记上下包络线均值为s1, x(t)与s1的差定义为:
$ {g_{1,1}}\left( t \right) = x\left( t \right) - {s_1} $
(2) 
Figure 2. The upper and lower envelopes of signal and mean value of the upper and lower envelops
对不同的初始信号, g1, 1(t)可能是一个IMF分量, 也可能不是。若是, g1, 1(t)就作为x(t)的第1阶IMF, 记为I(1)=g1, 1(t); 否则继续对g1, 1(t)进行以上操作。假设经过m次操作后得到了g1, m(t), g1, m(t)是否是一个IMF, 必须有一个可度量的参照。经研究发现, 它可用连续两个处理结果之间的标准差S来评判:
$ S = \sum\limits_{t = 0}^T {\left| {\frac{{{{\left| {{g_{1,\left( {m - 1} \right)}}\left( t \right) - {g_{1,m}}\left( t \right)} \right|}^2}}}{{{{\left[ {{g_{1,\left( {m - 1} \right)}}\left( t \right)} \right]}^2}}}} \right|} $
(3) 大量经验研究表明, S取值在0.2~0.3较为合适, 既可保证IMF的稳定性, 又可以使IMF具有相应的物理意义[12]。
当g1, m(t)满足S条件时, 记I(1)= g1, m(t)。然后将信号x(t)与其第1阶IMF的差值——r1(t)=x(t)-I(1)作为新的数据重复上述分解过程。假设经过n次分解后所得I(n)或者残余量r(t)小于某一阈值或者残余量已经成为单调函数, 则结束整个EMD分解过程。至此, 原始信号x(t)可表示为n阶IMF分量和残余量r(t)的和[8-10], 即:
$ x\left( t \right) = r\left( t \right) + \sum\limits_{k = 1}^n {I\left( k \right)} $
(4) 任一时域信号x(t)的希尔伯特变换y(t)定义为x(t)与$\frac{{\rm{1}}}{{{\rm{ \mathit{ π} }}t}}$的卷积[13-15], 即:
$ y\left( t \right) = x\left( t \right) \otimes \frac{1}{{{\rm{ \mathsf{ π} }}t}} = \frac{1}{{\rm{ \mathsf{ π} }}}p\int {\frac{{x\left( \tau \right)}}{{t - \tau }}{\rm{d}}\tau } $
(5) 式中, p代表柯西主值, 由x(t)及其希尔伯特变换可确定对应的解析信号z(t)为:
$ z\left( t \right) = x\left( t \right) + {\rm{i}}y\left( t \right) = a\left( t \right){{\rm{e}}^{{\rm{i}}\theta \left( t \right)}} $
(6) 式中, a(t)称为时域信号x(t)的瞬时幅值, θ(t)为其瞬时相位, 两者各由下式确定:
$ \left\{ \begin{array}{l} a\left( t \right) = \sqrt {{x^2}\left( t \right) + {y^2}\left( t \right)} \\ \theta \left( t \right) = \arctan \frac{{y\left( t \right)}}{{x\left( t \right)}} \end{array} \right. $
(7) 由相位函数求导可得信号的瞬时频率函数:
$ f\left( t \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\frac{{{\rm{d}}\theta \left( t \right)}}{{{\rm{d}}t}} $
(8) 对由原始信号x(t)通过EMD分解得到的每一阶IMF进行希尔伯特变换, 就可得到x(t)的一组由幅值和相位都随时间变化的组分表示:
$ x\left( t \right) = {\mathop{\rm Re}\nolimits} \sum\limits_{k = 1}^n {{a_k}\left( t \right){{\rm{e}}^{{\rm{i}}{\theta _k}\left( t \right)}}} $
(9) 上式中省去了残余量r(t), Re表示取所得结果的实数部分。更进一步可将相位函数表示为瞬时频率函数对时间的积分, 即:
$ H\left( {f,t} \right) = x\left( t \right) = {\mathop{\rm Re}\nolimits} \sum\limits_{k = 1}^n {{a_k}\left( t \right)\exp \left[ {{\rm{i}}2{\rm{ \mathsf{ π} }}\int {{f_k}\left( t \right){\rm{d}}t} } \right]} $
(10) 式中, H(f, t)是随时间和频率变化的信号幅度。这种由瞬时频率、瞬时幅值来表示原始光纤振动信号的方式叫做光纤振动信号的Hilbert谱表示法, 即光纤振动信号的时频谱。
-
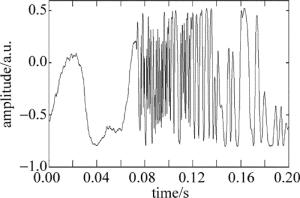
图 3展示的是光纤安防系统在调试过程中的一段包含有敲击光纤动作的信号, 信号在0.07s左右出现了剧烈的振荡, 而后逐渐趋于稳定。
Figure 3. Signal of optical fiber vibration
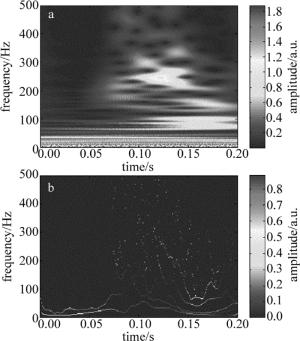
现在分别用连续小波变换和HHT绘制该信号的时频谱, 并进行分析。从图 4的时频谱可以看出, 连续小波变换和HHT得到的时频谱的频率随时间的分布大体相同, 两幅时频谱图都在0.05s和0.1s之间开始出现大量中高频分量, 与时域波形在0.07s左右开始剧烈振荡相一致, 表明这两种时频分析方法的适用性。整体来看, 小波变换和HHT都具有描述非平稳信号时频分布的能力, 都能够检测出信号突变发生的时间, 但小波变换得到的时频谱能量分布较分散, 谱线不够明显, 这是由于小波基长度受限并受测不准原理的制约, 发生了能量泄露, 出现了大量高频谐波成分, 造成了小波谱的分散[12]。HHT得到的时频分布很清晰, 较准确地刻画了信号的特征, 揭示了信号的时变特性。这是因为HHT的时间分辨率是固定的, 等于采样精度, 在高频和低频部分都一样[12]。综上所述, HHT比小波变换具有更高的时频分辨率, 更适合用来做非平稳信号的时频分析。
Figure 4. Time-frequency spectrum of CWT and HHT
基于以上小波变换和HHT的对比, 作者尝试采用HHT对实际采集到的光纤安防系统中传感光纤内的光信号进行简要分析。
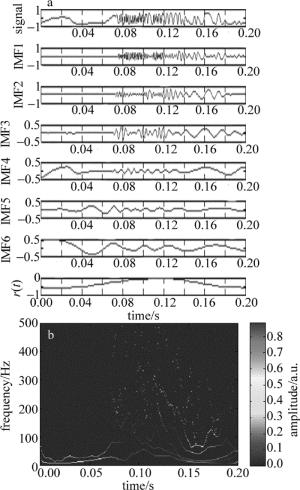
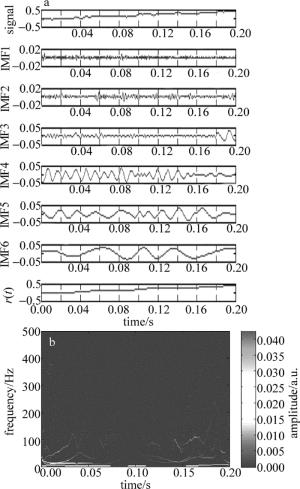
图 5为光纤在自然条件下受到应力作用时的一段光信号以及该信号的经验模态分解结果和时频谱。从原始信号以及EMD得到的前几阶IMF可以看出, 应力作用发生在0.07s左右, 信号开始振荡, 即信号相位变化剧烈。希尔伯特-黄变换理论的瞬时频率是对相位函数求导得到的, 所以对该信号进行HHT之后, 在这段时间内应该有较高的瞬时频率分量存在, 时频谱较好地证实了这一点。在0.07s之前, 时频谱中频率分量比较集中且全为低频, 这也与时域信号在这段时间内变化缓慢相对应; 在这之后, 时频谱高频区域出现了颜色较深的散点, 即有高频的瞬时分量存在, 呼应了时域信号的振荡特征。
Figure 5. Empirical mode decomposition and Hilbert-Huang spectrum of the invading signal
图 6为光纤在自然条件下的一段光信号以及该信号的经验模态分解结果和时频谱。从原始信号可以发现, 信号在该段时间内变化平缓, 虽然前几阶IMF有较多高频分量, 但是幅度都很小, 属于外界的高频噪声和干扰, 图 5中的IMF未出现, 是因为被幅值较大的振动分量掩盖了, 时域信号变化缓慢则时频谱中应多为低频分量。事实确实如此, 时频谱中低频分量占了绝大部分, 并且基本与时间轴平行即频率较稳定, 反应信号相位变化较平缓, 符合实际情况。
Figure 6. Empirical mode decomposition and Hilbert-Huang spectrum of the interference signal
由图 5与图 6的经验模态分解结果对比可以发现, 高阶IMF分量波形变化趋势比较相似, 同时两图的时频谱中部分低频分量的分布情况也比较接近, 两者相互呼应; 实际上这部分分量表征了系统本身和环境干扰的因素。在实际应用HHT进行系统信号分析设计时可结合具体实际情况, 在经验模态分解完成后剔除表征系统自身结构和外界干扰因素的IMF分量再进行后续分析, 从而可获得更高的区分度。
图 7反映的是入侵信号和干扰信号在进行经验模态分解剔除高阶IMF分量之后的时频谱, 对比之前未剔除高阶IMF分量的时频谱可发现, 大部分低频分量都已从图中消失。干扰信号的时频谱中还有少量散点, 这些散点的出现可能是由于在进行EMD分解过程中为了求取极值点包络多次使用了三次样条插值, 产生端点效应[15]导致了分析误差。但这些散点幅值都很小, 相对于入侵信号的幅值而言可以忽略不计, 对本次分析结构影响甚微, 故不在此过多涉及对端点效应的处理。在实际应用中, 一种简单的处理方式是在对连续信号进行分片处理时, 相邻片段之间留下合适长度的重叠部分, 以备在进行完EMD后可以丢弃每一阶IMF头部和尾部的部分数据以减弱端点效应的影响, 但这样做会增大极值点搜索、样条插值的运算量和系统开销, 在使用时需折中考虑。
Figure 7. Hilbert-Huang spectrum of the invading signal and the interference signal without higher-order IMF
-
作者分别采用小波变换和HHT对同一非平稳信号进行了时频分析, 结果表明, 在非平稳信号分析方面, HHT比小波变换具有更高的时频分辨率和更准确刻画信号时变特征的能力。应用HHT对传感光纤中产生的入侵信号和干扰信号进行了对比分析, 很好地把握住了入侵和干扰信号的时频特征, 更进一步证实了HHT的适用性和强大的时频分析能力, 同时这也表明, 采用HHT对传感光纤振动信号进行分析在理论上是行得通的。
HHT和CWT用于光纤振动信号分析的对比研究
Comparison study of optical fiber vibration signals using HHT and CWT
-
摘要: 为了提高光纤安防系统的准确预警能力，采用希尔伯特-黄变换法对光纤振动传感器信号产生原理和典型的光纤振动信号进行了分析，获得了传感器不同状态下信号的时频谱，并与通过连续小波变换得到的时频谱进行了对比分析。结果表明，希尔伯特-黄变换在光纤安防系统的时频分析中具有重要价值。Abstract: In order to improve the ability of accurate early warning of optical fiber security system, Hilbert-Huang transform (HHT) technology was adopted to analyze the principle of optical fiber vibration sensor's signal. Time-frequency spectrums of different signals were obtained. The comparison of time-frequency spectrums of optical fiber vibration signals by HHT and continuous wavelet transform (CWT) was analyzed. The results show that HHT has an important value in time-frequency analysis of optical fiber security system.
-
Figure 2. The upper and lower envelopes of signal and mean value of the upper and lower envelops
Figure 5. Empirical mode decomposition and Hilbert-Huang spectrum of the invading signal
a—empirical mode decomposition b—Hilbert-Huang spectrum
Figure 6. Empirical mode decomposition and Hilbert-Huang spectrum of the interference signal
a—empirical mode decomposition b—Hilbert-Huang spectrum
-
[1] ZHANG L N, LI F Ch, PENGB Q, et al. The basic principle of HHT method and application discussion[J]. Journal of East China Institute of Technology, 2013, 36(4):419-423(in Chinese). [2] ZHONG Y M, QIN Sh R, TANG B P. Study on the marginal spectrum in Hilbert-Huang transform[J]. Systems Engineering and Electronics, 2004, 26(9):1323-1326(in Chinese). [3] LIU Sh G, LI Z R, LIU Q. Study of self-mixing interference signal processing based on time-frequency analysis[J].Laser Technology, 2009, 33(6):626-629(in Chinese). [4] JIANG Sh Ch, CAO Y Q, SUI Q M, et al. Study on improved Hilbert-Huang transform-based ultra-narrow-bandwidth laser gas detection noise elimination[J]. Acta Optica Sinica, 2014, 34(1):1-6(in Chinese). [5] CAO L D, LIU X, QIAO F F, et al. Testing of pressure and temperature sensor based on all fiber Mach-Zehnder interferometer[J].Optics & Optoelectronics Technology, 2015, 13(3):34-37(in Chinese). [6] YU X M, LUO G M, ZHU Zh M, et al. The multi target recognition of intrusion signal of perimeter security with distributed fiber-optic sensor[J]. Opto-Electronic Engineering, 2014, 41(1):36-41(in Chinese). [7] FAN L Y, ZHAO R F, JIANG W W, et al. M-Z interferometer using a twin-core fiber for strain sensing[J]. Journal of Optoelectronics·Laser, 2010, 21(10):1488-1491(in Chinese). [8] OMID B, SOHEIL R. Enhanced Hilbert-Huang transform and itsapplication to modal identification[J]. The Structural Design of Tall and Special Buildings, 2014, 23(4):239-253. doi: 10.1002/tal.v23.4 [9] CHANG C C, HSIAO T C, HSU H Y. Frequency range extension of spectral analysis of pulse rate variability based on Hilbert-Huang transform[J]. Medical & Biological Engineering & Computing, 2014, 52(4):343-351. [10] PU L, YE Y T, WU Y F, et al. Laser interferometer signal processing based on empirical mode decomposition[J].Laser Technology, 2011, 35(3):299-301(in Chinese). [11] JI Ch P, ZHAO L N. Research of wave filter method of human sphygmus signal[J].Laser Technology, 2016, 40(1):42-46(in Chinese). [12] ZHANG Y P. HHT analysis and application of blasting vibration signal[M].Beijing:Metallurgical Industry Press, 2008:32-81(in Chinese). [13] HOU R N. Application of Hilbert transformin reconstruction of in-line digital holography[J].Laser Technology, 2013, 37(3):362-364(in Chinese). [14] GAO Y F, GUO H J, SONG X F, et al. Digital holographic phase reconstruction technology based on Hilbert transform[J].Laser Technology, 2015, 39(2):266-269(in Chinese). [15] LI X Y, HUANG Zh H, ZHANG H, et al. Phase analysis method based on Hilbert transform in dynamic speckle pattern interferometry[J]. Journal of Optoelectronics·Laser, 2015, 26(6):1111-1117(in Chinese). -
点击查看大图
图(7)
计量
- 文章访问数: 4581
- HTML全文浏览量: 2442
- PDF下载量: 344
- 被引次数: 0
