网站地图
下载:
-
1981年，LI和WOLF在研究光束聚焦特性时发现了焦移现象[1-2]。光束聚焦特性和焦移现象在近几十年来吸引了很多人的关注[3-20]。已有的研究结果表明，很多光束在聚焦过程中都存在焦移现象，例如空心高斯光束、部分相干平顶光束、聚焦拉盖尔-高斯光束、部分相干拉盖尔-高斯光束[5-6, 11, 15]。近年来，对这一现象的研究深入到微纳光学领域[8, 13]。例如YU等人在2012年研究了等离子体透镜中的焦移现象[8]。2015年HE等人研究了基于GaN高对比度光栅的2维透镜中的焦移[13]。大家熟知菲涅耳数和截断参量是影响焦移的重要参量，近些年很多研究结果表明, 光束的带宽也会影响焦移[9-10, 21-22]，这些结果给光束调控提供了一种新的方法。本文中研究了宽带厄米-高斯光束通过受光阑限制色散透镜系统的聚焦特性和焦移。首先推导了宽带厄米-高斯光束通过受光阑限制色散透镜系统的传输公式，然后以TEM11模和TEM22模为例讨论了带宽对宽带厄米-高斯光束的聚焦特性和焦移的影响，最后对所得结果进行了总结。
-
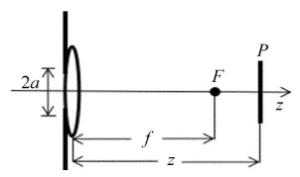
考虑宽带厄米-高斯光束通过一个如图 1所示的受光阑限制色散透镜系统。图中，2a是矩形硬边光阑的宽，F是焦点，f是焦距，P是考察面。基于惠更斯-菲涅耳衍射积分，可以得到宽带厄米-高斯光束中每一频率分量通过受光阑限制色散透镜系统的场分布为：
Figure 1. Schematic illustration of an apertured dispersion lens system
$ \begin{array}{c}{E_{m n}(x, y, z, \omega)=\frac{\mathrm{i} k}{2 {\rm{ \mathsf{ π} }} B} \exp (-\mathrm{i} k z) \times} \\ {\int_{-a}^{a} \int_{-a}^{a} E_{m n}\left(x_{0}, y_{0}, 0, \omega\right)\left\{\exp -\frac{\mathrm{i} k}{2 B}\left[A\left({x_0}^{2}+{y_0}^{2}\right)-\right.\right.} \\ {2\left(x_{0} x+y_{0} y\right)+D\left(x^{2}+y^{2}\right) ] \} \mathrm{d} x_{0} \mathrm{d} y_{0}}\end{array} $
(1) 式中, Emn(x0, y0, 0, ω)为初始入射光束，ω是频率，k是波数，m和n是模指数，(x0，y0)是初始横截面坐标，(x，y，z)是考察点坐标。ABCD为光束传输矩阵中的矩阵元，且传输矩阵为:
$ \boldsymbol{M}=\left[ \begin{array}{ll}{A} & {B} \\ {C} & {D}\end{array}\right]=\left[ \begin{array}{cc}{1-z / f(\lambda)} & {z} \\ {-1 / f(\lambda)} & {1}\end{array}\right] $
(2) 式中, 色散透镜的焦距为f(λ)=(n0－1)f0/[n(λ)－1]，其中n0和f0是与中心波长λ0相关的折射率和焦距，n(λ)是与波长λ相关的折射率，λ是波长。考虑图 1中色散透镜的材料为熔石英，折射率n(λ)定义见参考文献[23]。
假设初始入射光束可以表示为Emn(x0, y0, 0, ω)=Emn(x0, y0, 0)f(ω)，其中E0(x0, y0, 0)是入射光束的空间模式:
$ \begin{array}{c}{E_{m n}\left(x_{0}, y_{0}, 0\right)=\mathrm{H}_{m}\left(\sqrt{2} \frac{x_{0}}{w_{0}}\right) \mathrm{H}_{n}\left(\sqrt{2} \frac{y_{0}}{w_{0}}\right) \times} \\ {\exp \left[-\frac{\mathrm{i} k}{2 q_{0}}\left({x_0}^{2}+{y_0}^{2}\right)\right]}\end{array} $
(3) 式中, Hm()和Hn()为厄米多项式，w0是与基模高斯光束相关的束腰宽度，另有:
$ \frac{1}{q_{0}}=-\mathrm{i} \frac{\lambda}{{\rm{ \mathsf{ π} }} {w_0}^{2}}=\frac{2}{\mathrm{i} k {w_0}^{2}} $
(4) f(ω)是光束的频谱分布。考虑f(ω)在z＝0处为高斯分布，即:
$ f(\omega)=\frac{a_{\mathrm{G}}}{\sqrt{2} \omega_{0} \gamma} \exp \left[-\frac{{a_\mathrm{G}}^{2}\left(\omega-\omega_{0}\right)^{2}}{{\omega_0}^{2} \gamma^{2}}\right] $
(5) 式中, γ=Δω/ω0是相对带宽, ω0是中心频率, 高斯型频谱对应参量aG=(2ln2)1/2。
宽带光束通过受光阑限制的色散透镜后，光场分布由(1)式得到:
$ \begin{aligned} E_{m n}(x, y, z, t) &=\frac{1}{2 {\rm{ \mathsf{ π} }}} \int_{-\infty}^{\infty} E_{m n}(x, y, z, \omega) \times \\ & \exp (\mathrm{i} \omega t) \mathrm{d} \omega \end{aligned} $
(6) 式中, t=z/c，c是光速。
为简单起见，只考虑1维情况，2维情况可以类似得到。因此通过对空间部分积分后，得到TEM11模和TEM22模厄米-高斯光束的空间场分布为:
$ \begin{array}{c}{E_{11}(x, z)=\frac{2 S}{T^{2}}\left\{\exp \left[-\left(\sqrt{\alpha T}+\frac{Q x}{w_{0}}\right)^{2}\right]-\right.} \\ {\quad \exp \left[-\left(\sqrt{\alpha T}-\frac{Q x}{w_{0}}\right)^{2}\right]+\frac{\sqrt{{\rm{ \mathsf{ π} }}} Q W_{x} x}{w_{0}} \}}\end{array} $
(7) $ \begin{array}{c}{E_{22}(x, z)=\frac{S}{T^{3}}\left\{-4\left(\sqrt{\alpha T}-\frac{Q x}{w_{0}}\right) \times\right.} \\ {\exp \left[-\left(\sqrt{\alpha T}+\frac{Q x}{w_{0}}\right)^{2}\right]-4\left(\sqrt{\alpha T}+\frac{Q x}{w_{0}}\right) \times} \\ {\exp \left[-\left(\sqrt{\alpha T}-\frac{Q x}{w_{0}}\right)^{2}\right]+} \\ {\sqrt{{\rm{ \mathsf{ π} }}} W_{x}\left[2-T+4 Q^{2}\left(\frac{x}{w_{0}}\right)^{2}\right] \}}\end{array} $
(8) 其中,
$ T=1-\frac{\mathrm{i} {\rm{ \mathsf{ π} }} F_{\mathrm{w}}(z-f) / f}{z / f} $
(9) $ Q=\frac{\mathrm{i} {\rm{ \mathsf{ π} }} F_{\mathrm{w}}}{T^{1 / 2} z / f} $
(10) $ S=\frac{\mathrm{i} F_{\mathrm{w}}}{z / f} \exp \left[\left(Q^{2}-\frac{\mathrm{i} {\rm{ \mathsf{ π} }} F_{\mathrm{w}}}{z / f}\right)\left(\frac{x}{w_{0}}\right)^{2}\right] $
(11) $ W_{x}=\operatorname{erf}\left(\sqrt{\alpha T}-\frac{Q x}{w_{0}}\right)+\operatorname{erf}\left(\sqrt{\alpha T}+\frac{Q x}{w_{0}}\right) $
(12) 式中，α=(a/w0)2和Fw=w02/(λf)分别是截断参量和光束相关的菲涅耳数，erf()是误差函数。最后由Imn(x, z, t)=|Emn(x, z, t)|2得到宽带厄米-高斯光束通过色散透镜的光强分布。
-
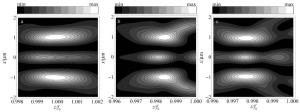
基于前面推导得到的结果，下面通过数值计算例研究了带宽对TEM11模厄米-高斯光束通过受光阑限制色散透镜系统的聚焦特性和焦移的影响。以下的计算示例中，因为仅考虑极大光强的变化，只讨论了t=z/c的光强分布。图 2是γ分别为0.05, 0.1, 0.15时宽带TEM11模厄米-高斯光束聚焦场的光强分布灰度图。计算参量为f0=1.6mm, λ0=800nm, α=4, Fw=196。下面计算示例的计算参量相同。图 2a表明, 带宽较小时, 光强极大几乎就在几何焦点上; 然而当带宽增大时，光强极大会偏离几何焦点，如图 2b所示; 当带宽进一步增大，这一效应更明显，如图 2c所示。图 2的结果表明, 带宽影响宽带TEM11模厄米-高斯光束聚焦场分布和实际焦点位置，光强极大与几何焦点的距离随着带宽的增大而增大。
Figure 2. Focused fields grayscale images of polychromatic TEM11 mode H-G beams
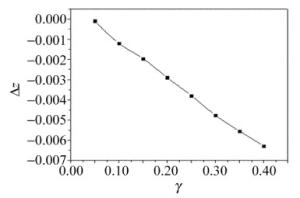
为清楚看出光强极大的位置变化，图 3中给出了相对焦移Δz=(z-f0)/f0随相对带宽的变化。从图中可以看出，在所讨论范围内，两者呈现线性关系，相对带宽越大光强极大位置变化越明显。例如γ=0.2时, |Δz|=0.0029，γ=0.4时, Δz增大为0.0063。焦移由光束的衍射现象引起[1-2]，宽带光束中不同频率分量衍射程度不一样导致焦移随带宽发生变化。
Figure 3. The relative focal shift of polychromatic TEM11 mode H-G beams vs. the relative bandwidth
-
图 4是γ分别为0.05, 0.1, 0.15时宽带TEM22模厄米-高斯光束通过受光阑限制色散透镜的光强分布灰度图。光强极大位置变化类似TEM22模厄米-高斯光束，即带宽增大时光强极大会偏离几何焦点，并且光强极大与几何焦点的距离随着增大。
Figure 4. Focused field grayscale images of polychromatic TEM22 mode H-G beams
在图 5中给出了宽带TEM22模厄米-高斯光束的相对焦移Δz随相对带宽的变化，为便于比较，图中保留了宽带TEM11模厄米-高斯光束的曲线。图中结果表明，两者相对焦移随相对带宽的变化是一样的。但有趣的是，宽带TEM22模厄米-高斯光束的相对焦移绝对值|Δz|并不是一直大于TEM11模的|Δz|。从计算结果看:γ < 0.25时, 前者大于后者；而γ>0.25后, 后者会稍大于前者。例如，γ=0.15时, TEM22模的|Δz|=0.00237，而TEM11模的|Δz|=0.00196，前者比后者大17.3%;当γ=0.35时，两者分别为0.00549和0.00556，后者反而比前者大1.3%。只不过后者比前者大时两者的差距很小，并随着带宽增大, 差距趋于零。
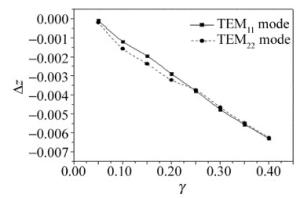
Figure 5. The relative focal shift of polychromatic TEM11 mode H-G beams and TEM22 mode H-G beams vs. the relative bandwidth
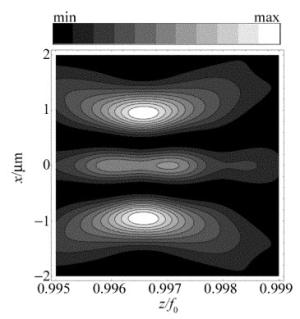
作者认为:图 5中的这种变化主要是由宽带TEM22模厄米-高斯光束轴上光强变化引起。从图 4c可以看出, 轴上有两个光强极大，即光强主极大和光强次极大，且光强主极大位于图中左边而光强次极大位于右边。然而当γ由图 4c中的0.15增大到图 6中的0.22，光强主极大位于图中右边而光强次极大位于左边，与图 4c相反，即轴上的光强主极大从一个位置跃变到另一个位置。这一变化影响了宽带TEM22模厄米-高斯光束的聚焦光强分布，从而导致了在γ较大时, TEM11模和TEM22模的焦移不一样。
Figure 6. Focused fields grayscale images of polychromatic TEM22 mode H-G beams when γ=0.22
-
作者研究了宽带TEM11模和TEM22模厄米-高斯光束通过受光阑限制色散透镜的聚焦特性和焦移。通过数值计算例分析讨论了带宽对光强分布和光强极大位置的影响，结果表明，带宽也是影响焦移的重要因素。TEM11模和TEM22模的焦移量都会随带宽的增大而增大。然而两者焦移量之间的相对大小并不确定，前者既可能大于后者，也可能小于后者。这一现象主要缘于带宽变化会导致TEM22模厄米-高斯光束轴上光强主极大从一个位置跃变到另一个位置。文中的研究结果有助于宽带厄米-高斯光束的应用。
色散透镜系统中宽带厄米-高斯光束的焦移
Focal shift of polychromatic Hermite-Gaussian beams in dispersion lens system
-
摘要: 为了了解带宽对厄米-高斯光束的聚焦特性和焦移的影响，采用衍射积分推导了TEM11模和TEM22模厄米-高斯光束通过受光阑限制色散透镜的传输公式，并利用数值计算对聚焦光强分布进行了研究，分析了带宽对两种模式焦移的影响。结果表明，TEM11模和TEM22模厄米-高斯光束的焦移量都会随带宽增大而增大，但两者的大小依赖相对带宽；当相对带宽小于0.25时，TEM22模焦移量大于TEM11模焦移量，然而相对带宽大于0.25时，后者会稍大于前者；带宽变化使TEM22模轴上光强主极大和次极大发生消长，从而引起轴上光强极大位置发生跃变。该研究结果对宽带厄米-高斯光束的应用具有一定的参考价值。Abstract: In order to know effect of bandwidth on the focused properties and focal shift of Hermite-Gaussian (H-G) beam, propagation formula of H-G beams passing through a dispersion lens system with polychromatic TEM11 mode and TEM22 mode was obtained by using diffraction integral. The focused intensity distribution was studied by numerical calculation. The effect of bandwidth on focal shift of both modes were analyzed. The results show that the focal shifts of H-G beams with TEM11 mode and TEM22 mode increase with the increase of the bandwidth and depend on the relative bandwidth. Focal shift of TEM22 mode is greater than that of TEM11 mode when relative bandwidth is smaller than 0.25 whereas the latter is somewhat greater than the former when relative bandwidth exceeds 0.25. The principle maximum intensity and the secondary maximum intensity of TEM22 mode on the axis compete each other with the vary of bandwidth and then the axial primary maximum intensity transits from one place to another. The results are helpful for further application of the polychromatic H-G beams.
-
Key words:
- laser physics /
- focal shift /
- dispersion lens /
- bandwidth
-
Figure 2. Focused fields grayscale images of polychromatic TEM11 mode H-G beams
a—γ=0.05 b—γ=0.1 c—γ=0.15
Figure 3. The relative focal shift of polychromatic TEM11 mode H-G beams vs. the relative bandwidth
Figure 4. Focused field grayscale images of polychromatic TEM22 mode H-G beams
a—γ=0.05 b—γ=0.1 c—γ=0.15
Figure 5. The relative focal shift of polychromatic TEM11 mode H-G beams and TEM22 mode H-G beams vs. the relative bandwidth
-
[1] LI Y, WOLF E. Focal shifts in diffracted converging spherical waves[J]. Optics Communications, 1981, 39(4):211-215. doi: 10.1016/0030-4018(81)90108-5 [2] LI Y, WOLF E. Focal shift in focused truncated Gaussian beams[J]. Optics Communications, 1981, 42(3):151-156. [3] MARTÍNE-CORRAL M, CABALLERO M T, MUÑOZ-ESCRIVÁ L, et al. Focal-shift formula in apodized non-telecentric focusing systems[J]. Optics Letters, 2001, 26(19):1501-1504. doi: 10.1364/OL.26.001501 [4] KEIR C N, ELIO A A, STEVEN M B. Measurement of the effective focal shift in an optical trap[J]. Optics Letters, 2005, 30(22):1318-1320. [5] GHAFARY B, SIAMPOOR H, ALAVINEJAD M. Focal shift for off-axial partially coherent flat topped beams passing a thin lens[J]. Optics & Laser Technology, 2010, 42(5):755-759. [6] YUN M J, LIANG W, KONG W J, et al. Transverse superresolution and focal shift with rotational tunable phase mask[J]. Optics Communications, 2010, 283(10):2079-2083. doi: 10.1016/j.optcom.2010.01.039 [7] ALAVINEJAD M, ROWSHANI A R, GHAFARY B. Focal shift and focal switch of phase-lock partially coherent flat-topped array beams passing through an aligned and misaligned lens system with aperture[J]. Optics and Lasers in Engineering, 2012, 50(9):1341-1349. doi: 10.1016/j.optlaseng.2012.02.006 [8] YU Y T, ZAPPE H. Theory and implementation of focal shift of plasmonic lenses[J]. Optics Letters, 2012, 37(9):1592-1594. doi: 10.1364/OL.37.001592 [9] PENG R W, LI L, LI Y J, et al. Positive and negative focal shifts of an apertured supercontinuum laser with rectangular spectrum[J]. Optics Communications, 2012, 298/299(1):34-36. [10] PENG R W, LI L, LI Y J, et al. Effect of spectrum property on a focused supercontinuum laser[J]. Optics Communications, 2013, 309(15):26-29. [11] REN Zh Ch, QIAN Sh X, TU Ch H, et al. Focal shift in tightly focused Laguerre-Gaussian beams[J]. Optics Communications, 2015, 334(1):156-159. [12] PENG Ch B. Observation of focal point shift in solid immersion mi-rror[J]. Optics Express, 2015, 23(2):1498-1504. doi: 10.1364/OE.23.001498 [13] HE Sh M, WANG Zh H, LIU Q F, et al. Study of focal shift effect in planar GaN high contrast grating lenses[J]. Optics Express, 2015, 23(23):29360-29368. doi: 10.1364/OE.23.029360 [14] MA R, LI Y T, LIU Y M, et al. Focal shift of nano-optical lens a-ffected by periodic resonance with substrate[J]. IEEE Photonics Journal, 2016, 8(6):4502309. [15] ZHANG M H, CHEN Y H, LIU L, et al. Focal shift of a focused partially coherent Laguerre-Gaussian beam of all orders[J]. Journal of Modern Optics, 2016, 63(21):2226-2264. doi: 10.1080/09500340.2016.1191687 [16] ZHANG M H, CHEN Y H, CAI Y J, et al. Effect of the correlation function on the focal shift of a partially coherent beam[J]. Journal of the Optical Society of America, 2016, A33(12):2509-2515. [17] PENG J, CUI Zh F, QU J. Solution and focus property of the nonparaxial vector beams in the parabolic coordinates[J].Laser Technology, 2014, 38(5):703-708(in Chinese). [18] ZHAO Q, HAO H Y, FAN H Y, et al. Focusing characteristics of partially coherent cosh-Gaussian beams propagating through turbulent atmosphere[J]. Laser Technology, 2016, 40(5):750-755(in Chinese). [19] ZHANG B Y, PENG R W, ZHANG W. Bandwidth-induced focal switch in broadband laser with rectangular spectrum[J]. Laser Technology, 2017, 41(1):138-140(in Chinese). [20] ZHAO J H, WANG Q, ZHU B W, et al. Compact focusing properties of radial vector beam with vortex phase encoding[J]. Laser Technology, 2017, 41(2):187-190(in Chinese). [21] JI X L, ZHANG E T, LÜ B D. Spreading of spatially partially coherent polychromatic beams in atmospheric turbulence[J]. Optik, 2008, 119(14):689-694. doi: 10.1016/j.ijleo.2007.01.016 [22] MAO H D, ZHAO D M. Second-order intensity-moment characteristics for broadband partially coherent flat-topped beams in atmospheric turbulence[J]. Optics Express, 2010, 18(2):1741-1755. doi: 10.1364/OE.18.001741 [23] MALITSON I H. Interspecimen comparison of the refractive index of fused silica[J]. Journal of the Optical Society of America, 1965, 55(10):1205-1209. doi: 10.1364/JOSA.55.001205 -
点击查看大图
图(6)
计量
- 文章访问数: 7503
- HTML全文浏览量: 5186
- PDF下载量: 23
- 被引次数: 0
