网站地图
下载:
-
光纤布喇格光栅(fiber Bragg grating，FBG)因其具有体积小、重量轻、耐腐蚀、不易受电磁干扰、可适用于恶劣环境等优点已被广泛地应用在桥梁、石化、航空航天、医疗等领域[1-5]，用来测量温度、应变、压力、振动、位移、电磁等多种物理量[6-9]。当FBG所处的外界环境发生变化时，FBG的中心波长也会发生偏移，根据波长的偏移量，就可计算出外界物理量的变化[10]。如何更加精确地解调出波长的偏移量，是目前的研究重点和亟待解决的问题。
基于可调谐法布里-珀罗(Fabry-Perot，F-P)滤波器解调法是靠三角波电压来驱动粘贴在F-P腔一侧的压电陶瓷(piezoelectric ceramics, PZT)，使PZT发生微小形变，导致F-P腔腔长发生改变，进而使透过的中心波长发生变化。但是由于压电陶瓷的蠕变性、迟滞性以及温度变化等原因，导致F-P滤波器的驱动电压与透射波长不成线性，从而使波长的解调不精确，造成较大的测量误差[11-14]。目前，已经存在的校正方法有很多，比如参考FBG法、F-P标准具法、气体吸收谱线校正法等。参考FBG法虽然结构简单，但是参考点少，对可调谐F-P滤波器的标定不够精确[15-16]。F-P标准具法可以比参考FBG法引入更多的参考点，但是在温度的影响下，F-P标准具的峰值波长也会漂移[17]。气体吸收谱线校正法可以提供稳定的波长校准，但是覆盖的波长范围较小，峰值的提取比较难[18]。为了更好地解决这个问题，本文中提出了一种高精度波长标定方法，就是加入可以输出均匀锯齿波的F-P标准具，由于标准具也会随外界环境的影响整体漂移，通过温补参考光栅对标准具进行标定，达到提高解调的稳定性[19-21]。
-
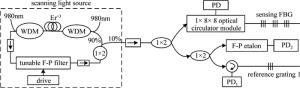
基于F-P标准具和温补参考光栅的解调系统如图 1所示。该系统的光源是采用可调谐环形腔激光器。输出的光分别进入传感通道、参考通道以及F-P标准具通道。传感通道的波分复用器(wavelength division multiplexing, WDM)可以实现对多个通道的同时测量，达到分布式测量的目的。当传感光栅的布喇格波长等于可调谐F-P滤波器波长时，光电探测器(photodetector, PD)输出峰值信号。将PD, PD1和PD2输出的峰值信号经多路采集卡，传输到上位机，进行数据处理。本系统采用的是参考光栅、F-P标准具以及传感通道分开在3个单独的通道。参考光栅通过温度补偿封装，使光栅的波长随温度漂移量极低，温度系数可小于1pm/℃，所以参考光栅在不受应力的情况下，可忽略环境温度对波长的影响，用其来标定F-P标准具。
Figure 1. Demodulation system of fiber Bragg grating
-
可调谐F-P滤波器的驱动电压与透射波长的关系曲线图如图 2所示。从图中可以看到，两次测量的可调谐F-P滤波器的驱动电压与透射波长是不同的曲线，无法拟合出单一曲线来表示它们的关系。虽然可调谐F-P滤波器的驱动电压与透射波长不成线性关系，但是可以对其进行分段处理，在较小段范围内，进行线性插值，就可以得到传感FBG的波长值，消除非线性的影响。
Figure 2. Relationship between driving voltage and F-P filter transmission wavelength
三角波驱动F-P腔时，激光器输出窄带光源，同时扫描传感通道、参考通道和标准具通道。当窄带光源与FBG的波长相等时，输出的光强最大，记录下此时所对应的驱动电压值。虽然F-P滤波器的透射波长与驱动电压不成线性，但是在F-P标准具的两个梳状齿之间的较小范围内，可以认为是线性的。已知参考光栅的波长为λ，驱动电压值为V，与它相邻的标准具的两个峰值点分别为Pi和Pi+1，驱动电压是已知的，分别为VPi和VPi+1，设波长分别为λPi和λPi+1，所以有方程：
$ \frac{{{\lambda }_{{{P}_{i+1}}}}-{{\lambda }_{{{P}_{i}}}}}{{{V}_{i+1}}-{{V}_{{{P}_{i}}}}}=\frac{\lambda -{{\lambda }_{{{P}_{i}}}}}{V-{{V}_{{{P}_{i}}}}}~ $
(1) 由于标准具的每两个峰值点之间的频率间隔为一个自由光谱范围(free spectral range, FSR)FFSR，所以：
$ {{F}_{\text{FSR}}}={{\lambda }_{{{P}_{i+1}}}}-{{\lambda }_{{{P}_{i}}}} $
(2) 标准具的峰值点Pi的波长为：
$ {{\lambda }_{{{P}_{i}}}}=\lambda +\frac{V-{{V}_{{{P}_{i}}}}}{{{V}_{{{P}_{i+1}}}}-{{V}_{{{P}_{i}}}}}\times {{F}_{\text{FSR}}} $
(3) 该系统选用的标准具的频率为100GHz，FSR为0.8nm。记峰值点Pi在标准具中的序号为k，则第n个峰值的波长为：
$ {{\lambda }_{n}}={{\lambda }_{{{P}_{i}}}}-\left( k-n \right){{F}_{\text{FSR}}} $
(4) 根据(4)式，标准具的所有峰值点的波长都可以计算出来。在传感通道上，滤波器输出的波长与传感光栅的中心波长相等时，会出现峰值输出，检测出此时所对应的驱动电压，并判断该电压在标准具中的具体位置，相邻的两个峰值的波长可以根据公式计算出。使用线性插值计算传感光栅的波长为：
$ {{\lambda }_{\text{B}}}=\frac{({{V}_{\text{B}}}-{{V}_{i}})\left( {{\lambda }_{i+1}}-{{\lambda }_{i}} \right)}{\left( {{V}_{i+1}}-{{V}_{i}} \right)}+{{\lambda }_{i}}~ $
(5) 式中，λB为Bragg光栅的中心波长；VB为传感光栅峰值输出对应的驱动电压值；Vi和Vi+1分别是相邻两个标准具峰值输出对应的驱动电压，满足Vi≤VB≤Vi+1；λi+1和λi是传感光栅相邻的两个标准具峰值的波长。
-
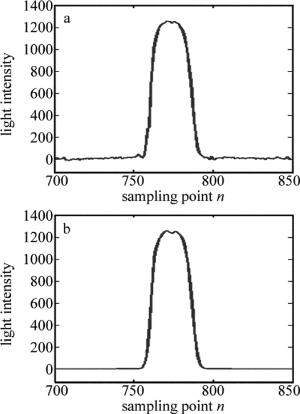
由于受到电路、光路以及采集卡等各因素的影响，使得采集到的FBG反射谱中含有各种噪声。为了更加准确地找到FBG反射谱的中心波长，首先要进行的就是去噪处理。本文中采用10次滑动平均滤波，滤波前后对比图如图 3所示。
Figure 3. Effect diagram of moving average filter
通过同一采集卡采集到的反射谱基本上是不变的，只是中心波长位置发生了移动。因此，无论光栅中心波长是向左移动还是向右移动，都可以通过频谱相关算法计算采集到的FBG反射谱与所设定的原始标准光谱的相似性来判断。但是频谱相关算法的计算量很大，需要花费一定的计算时间。所以本文中采用基于强度阈值之后的频谱相关算法进行寻峰。
采用适当的强度阈值，即将大于某强度阈值的采样点找出来，只对这些点进行互相关处理，而不是对所有的点计算，这样不仅可减少数据的运算量，提高数据的实时处理的能力，还可减小误差值。首先算出所有点强度的平均值，然后以平均值为基准进行阈值选择。阈值选择后的图像如图 4所示。
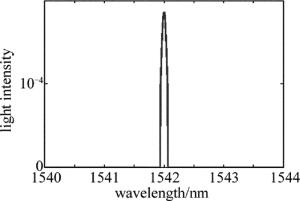
Figure 4. Relationship between light intensity and wavelength after the selection of intensity threshold
光栅的温度改变或者受到应力的作用时，光栅的波长会发生移动。经过滤波和强度阈值后的图像如图 5所示。
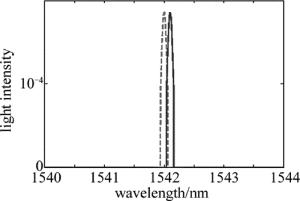
Figure 5. Relationship between light intensity and wavelength after the selection of intensity threshold
将图 5的两个FBG反射谱进行互相关计算，找出最大相关值点所对应的波长值，也就得到了中心波长的漂移。
-
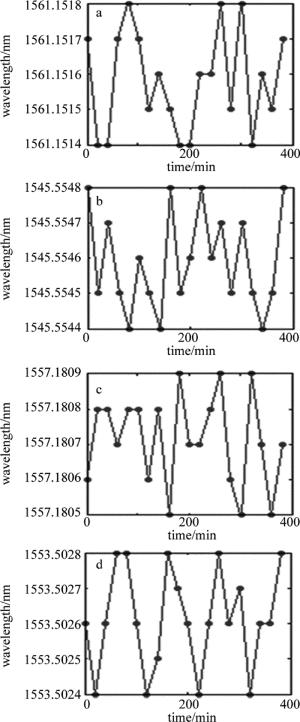
首先根据图 1所示的解调系统搭建实验平台。可调谐F-P滤波器的驱动电压范围是5V~19V，F-P标注具的FSR为0.4nm。在传感通道上接4个光栅，相同温度下，通过对不同时间光栅的波长进行测量，来测试系统的分辨率。将光栅放在25℃的恒温环境中，保证光栅不受温度和应力的影响。对4个光栅的波长分别进行测量，每隔20min测量、记录一次数据，一共记录20组数据。从图 6中可以看出，4个光栅的波长漂移均在0.4pm以内。
Figure 6. Measurement results after wavelength shift
为了验证系统的重复性，将传感光栅放在恒温水槽中进行高低温实验。恒温水槽的精度温度波动度可达±0.05℃。将水槽的温度从25℃升至30℃，再从30℃下降到25℃，每次变动1℃。为了保证测量的准确性和合理性，且保持20min，待温度稳定后，记录一次波长值，整个过程进行10次，如图 7所示。从图 7中可以看到，在10次高低温循环实验中，各个温度点上的解调波长没有明显的漂移或迟滞等现象，表明解调系统具有很好的重复性。
Figure 7. Demodulation data and local magnification in the process of temperature changing
将两个温度传感光栅放在恒温水槽中，使其不受应力的作用。将恒温水槽的温度从25℃逐渐升温到80℃，每次间隔5℃。保持30min记录一次波长值。FBG反射波长与温度的关系曲线如图 8所示。
Figure 8. Relationship between temperature and wavelength
从图 8中可以看出，FBG反射波长与温度具有良好的线性关系，线性度达到99.90%以上。
-
本文中采用可调谐环形腔激光器作为光源，同时扫描传感通道、参考通道、F-P标准具通道3个单独的通道。为了消除由于PZT的非线性与不稳定性对测量带来的影响，利用F-P标准具校准可调谐F-P滤波器的输出波长，并用温补参考光栅对F-P标准具进行标定。在标准具两个梳状齿之间利用插值的方法，得到位于两个梳状齿之间传感光栅的中心波长，提高了解调的精度。通过中值滤波加滑动平均滤波的方法和基于强度阈值的频谱相关算法，对数据进行处理。实验结果表明，波长的稳定性达到0.4pm，温度与波长的线性度高于99.90%。与未分开在单独通道且用气体标定的系统相比，本系统具有高稳定性、高线性度以及较好的重复性等优点。
F-P标准具和参考光栅相结合的高稳定性FBG解调系统
High stability FBG demodulation system combining F-P etalon with reference grating
-
摘要: 为了提高光纤布喇格光栅（FBG）解调系统的稳定性和准确性，避免由于压电陶瓷的迟滞性、蠕变性以及温度变化引起的法布里-珀罗（F-P）滤波器驱动电压与透射波长不成线性的问题，采用了可调谐环形腔激光器作为扫描光源，与F-P标准具、温补参考光栅、传感光栅3个单独的通道结构相结合的FBG解调方法。通过理论分析和实验验证，选择中值滤波加滑动平均滤波的方法滤除噪声，采用基于强度阈值的频谱相关寻峰算法更加准确地找到反射谱峰值的位置。结果表明，每个通道单独分开的解调方案的波长长期稳定性可达0.4pm，温度与波长的线性度高于99.90%。该系统能够实现对温度、应变等参量的稳定性的测量。Abstract: In order to improve the stability and accuracy of a fiber Bragg grating(FBG) demodulation system and avoid the problem of nonlinearity of driving voltage and transmission wavelength of a Fabry-Perot(F-P) filter caused by hysteresis, vermicular and temperature changes of the piezoelectric ceramic, a FBG demodulation method was introduced combining with F-P etalon, temperature-compensated reference grating and sensing grating in three separate channels with a tunable ring cavity laser as scanning light source. The method of median filtering and moving average filtering was selected to filter the noise. A spectral correlation peak-seeking algorithm based on intensity threshold was used to find the location of peak value of reflection spectrum more accurately. Through theoretical analysis and experimental verification, the results show that wavelength long-term stability of demodulation scheme with each separated channel can reach 0.4pm and the linearity between temperature and wavelength is higher than 99.90%. The system can measure the stability of the parameters such as temperature and strain.
-
Key words:
- gratings /
- F-P filter /
- F-P etalon /
- reference grating /
- tunable ring cavity lasers
-
Figure 3. Effect diagram of moving average filter
a—before filtering b—after filtering
Figure 4. Relationship between light intensity and wavelength after the selection of intensity threshold
Figure 5. Relationship between light intensity and wavelength after the selection of intensity threshold
Figure 7. Demodulation data and local magnification in the process of temperature changing
-
[1] BAI W, YANG M, DAI J, et al. Novel polyimide coated fiber Bragg grating sensing network for relative humidity measurements[J]. Optics Express, 2016, 24(4):3230-3237. doi: 10.1364/OE.24.003230 [2] ZHANG Y N, XIAO H, SHEN L Y. Coordinate point fitting for fiber grating curve reconstruction algorithm[J]. Optics and Precision Engineering, 2016, 24(9):2149-2157(in Chinese). doi: 10.3788/OPE. [3] YANG Y Q, YANG Q, GE W, et al. Temperature automatic compensation giant magnetostrictive material Bragg grating fiber current sensor[J].Optics and Precision Engineering, 2016, 24(10):2377-2383(in Chinese). doi: 10.3788/OPE. [4] RORIZ P, CARVALHO L, FRAZÃO O, et al. From conventional sensors to fibre optic sensors for strain and force measurements in biomechanics applications:a review[J]. Journal of Biomechanics, 2014, 47(6):1251-1261. doi: 10.1016/j.jbiomech.2014.01.054 [5] GUO Y X, XIONG L, KONG J Y, et al. Sliding fiber Bragg grating displacement sensor[J].Optics and Precision Engineering, 2017, 25(1):50-58(in Chinese). doi: 10.3788/OPE. [6] YI Z, DONG X P. Demodulation of the FBG temperature sensor with the tunable twin-core fiber[J]. Microwave and Optical Technology Letter, 2011, 53(1):81-84. doi: 10.1002/mop.v53:1 [7] ZHANG L, LIU Y M, GAO X L, et al. High temperature strain sensor based on a fiber Bragg rating and rhombus metal structure[J]. Applied Optics, 2015, 54(28):109-112. doi: 10.1364/AO.54.00E109 [8] PENG H, ZHOU B H, WANG H, et al. A new method for resolving the influence of circular birefringence in FBG weak pressure sensor[J]. Measurement, 2014, 58:280-285. doi: 10.1016/j.measurement.2014.08.050 [9] JIANG S C. Study of three-component FBG vibration sensor for simultaneous measurement of vibration, temperature, and verticality[J]. Journal of Sensors, 2015, 2015(29):1-9. [10] KERSEY A D, DAVIS M A, PATRICK H J. Fiber grating sensor[J]. Journal of Lightwave Technology, 1997, 15(8):1442-1463. doi: 10.1109/50.618377 [11] LI Y, ZHANG Sh L. A novel fiber Bragg grating sensor interrogation system utilizing a tunable Fabry-Perot filter[J]. Laser Technology, 2005, 29(3):237-240(in Chinese). [12] LIANG X, LIU T G, LIU K, et al. Method of real-time calibration for tunable optical filter nonlinearity[J]. Chinese Journal of Lasers, 2010, 37(6):1445-1449(in Chinese). doi: 10.3788/CJL [13] RIBEIRO B D A, WERNECK M M, SILVA-NETO J L D. Novel optimization algorithm to demodulate a PZT-FBG sensor in AC high voltage measurements[J]. IEEE Sensors Journal, 2013, 13(4):1259-1264. doi: 10.1109/JSEN.2012.2232290 [14] MEI J W, XIAO X Sh, YANG Ch X. Nonlinear optimization of scanning laser scanning and its application in fiber grating demodulation[J]. Optics and Precision Engineering, 2014, 22(11):2888-2893(in Chinese). doi: 10.3788/OPE. [15] LIU K, JING W C, PENG G D, et al. Investigation of PZT driven tunable optical filter nonlinearity using FBG optical fiber sensing system[J]. Optics Communications, 2008, 281(12):3286-3290. doi: 10.1016/j.optcom.2008.02.034 [16] WANG P, ZHAO H, LIU J, et al. Dynamic real-time calibration method for fiber Bragg grating wavelength demodulation system based on tunable fabry-Perot filter[J]. Acta Optica Sinica, 2015, 35(8):0806006(in Chinese). doi: 10.3788/AOS [17] WANG J H, XU X M, DING J F, et al. Based on the method of Fabry-Perot etalon and calibration of the fiber Bragg grating wavelength demodulation system[J].Acta Photonica Sinica, 2016, 45(6):0606003(in Chinese). doi: 10.3788/gzxb [18] QIAO X G, WANG Y, FU H W, et al. High-accuracy real time calibration of tunable Fabry-Perot filter on large range[J]. Acta Optica Sinica, 2008, 28(5):852-855(in Chinese). doi: 10.3788/AOS [19] YANG G, XU G L, TU G J, et al. The high precision of FBG wavelength demodulation system based on spectrum partition[J].Chinese Journal of Lasers, 2015, 42(4):0405001(in Chinese). doi: 10.3788/CJL [20] LI Y Q, AN Y, YAO G Zh. The analysis and design of reference wavelength of FBG wavelength demodulation system[J].Optical Device, 2013, 8(4):11-14(in Chinese). [21] LI Zh Y, ZHOU Z D, TONG X L, et al. Research of high-speed large-capacity fiber Bragg grating demodulator[J]. Acta Optica Sini-ca, 2012, 32(3):306007(in Chinese). doi: 10.3788/AOS -
点击查看大图
图(8)
计量
- 文章访问数: 5835
- HTML全文浏览量: 3530
- PDF下载量: 145
- 被引次数: 0
