-
光声成像是过去20年来新兴的一种生物医学成像模态[1-6],它是一种光激发的混合成像模式,将光学成像和超声成像的优点结合了起来。一方面,在光声成像中用来重建图像的信号是超声信号,生物组织对超声信号的散射要比光学信号低2~3个数量级,因此相比纯光学成像,光声成像具有更深的成像深度和更高的空间分辨率;另一方面,光声成像根据不同组织对可见光、近红外光的选择性吸收,利用特定波长的激光脉冲对组织进行照射,成像的是在生物组织内被吸收的激光脉冲能量的分布,其一定程度上反映组织的吸收系数分布,这在纯超声成像中是无法做到的,因此相比纯超声成像,光声成像具有更高的光学对比度。
目前光声成像系统逐步向实时[7-9]、多维度[10-11]方向发展,因此采用单通道、单超声换能器系统由于存在系统鲁棒性差,需进行多次调整,单切面扫描时间过长等问题已不能够适应最新的发展趋势,所以必须研发能够高速多通道采集光声信号的高鲁棒性光声成像系统。而国际上已有很多开展在体光声断层成像方面的研究[12-21], 这些研究中成像系统的实现方式和目的各有不同,有的采用线性阵列[12, 15-17],有的主要开展离体的成像实验[13-14]; 参考文献[18]中主要针对光声显微成像方面; 参考文献[19]中采用的是一个垂直放置的弧形的换能器阵列,需要旋转成像对象才能获得3维的图像; 参考文献[20]和参考文献中采用弧形换能器阵列开展实时在体实验,但是由于其激光是垂直激发成像对象即正交模式,所以只适合小动物脑部成像,不适合断层成像;参考文献[7]和参考文献[8]中专门设计用于开展临床实验。因此本文中采用背向传输模式, 即超声换能器阵列与脉冲激光在同一侧, 这样就保证了在成像不同断层时不会对成像对象带来影响, 同时利用美国国家仪器公司(Naticmal Instruments, NI)的数据采集模块和多通道弧形聚焦换能器来构建多通道采集模块以实现光声断层成像数据的高速采集, 最后利用正则化优化的基于模型的重建算法对原始数据进行高质量的图像重建。
-
光声信号的产生是由于短时脉冲激光照射生物组织,组织中的吸收体吸收一部分能量使得局部温度升高,导致发生热弹性膨胀,从而产生超声波。在满足热力限制和应力限制的条件下,声压p(r, t)满足的关系[22]:
$ \begin{array}{l} \frac{{{\partial ^2}p(\mathit{\boldsymbol{r}}, t)}}{{\partial {t^2}}} - {c^2}\left( \mathit{\boldsymbol{r}} \right)\rho \left( \mathit{\boldsymbol{r}} \right)\nabla \cdot \\ \left[ {\frac{1}{{\rho \left( \mathit{\boldsymbol{r}} \right)}}\nabla p(\mathit{\boldsymbol{r}}, t)} \right] = \mathit{\Gamma }\frac{{\partial H(\mathit{\boldsymbol{r}}, t)}}{{\partial t}} \end{array} $
(1) 式中,r为3维空间内的位置坐标; t表示时间; c(r)和ρ(r)分别为组织的声速和密度; Γ为无量纲格鲁内森参量; H(r, t)是热源函数,代表单位时间、单位体积内的热量。假设生物组织的密度是均匀的,即在成像区域内ρ(r)是常数,并假设声速是均匀的,即c(r)为常数c,另外热源函数还可以表示为H(r, t)=H(r)×H(t),其中H(r)表示单位体积内沉积的热能量,H(t)表示脉冲激光光强随时间的分布函数。在实际成像过程中脉冲激光脉宽很短,理论上光强函数可假设为一个脉冲函数,即H(t)=δ(t),因此(1)式可表示为:
$ \frac{{{\partial ^2}p(\mathit{\boldsymbol{r}}, t)}}{{\partial {t^2}}} - {c^2}{\nabla ^2}p(\mathit{\boldsymbol{r}}, t) = \mathit{\Gamma }H\left( \mathit{\boldsymbol{r}} \right)\frac{{\partial \delta \left( t \right)}}{{\partial t}} $
(2) (2) 式可以等价地表示为一个初始值问题:
$ \frac{{{\partial ^2}p(\mathit{\boldsymbol{r}}, t)}}{{\partial {t^2}}} - {c^2}{\nabla ^2}p(\mathit{\boldsymbol{r}}, t) = 0 $
(3) 初始条件为:
$ \left\{ \begin{array}{l} p(\mathit{\boldsymbol{r}}, t)\left| {_{t = 0} = \mathit{\Gamma }H\left( \mathit{\boldsymbol{r}} \right)} \right.\\ \frac{{\partial p(\mathit{\boldsymbol{r}}, t)}}{{\partial t}}\left| {_{t = 0} = 0} \right. \end{array} \right. $
(4) 上述初始值问题可以通过求解一个泊松类型的积分[23]而得到一个解析解:
$ p(\mathit{\boldsymbol{r}}, t) = \frac{\mathit{\Gamma }}{{4{\rm{ \mathit{ π} }}c}}\;\frac{\partial }{{\partial t}}\int_{S'\left( {\mathit{\boldsymbol{r}}, t} \right)} {\frac{{H\left( {\mathit{\boldsymbol{r'}}} \right)}}{{\left| {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r'}}} \right|}}} {\rm{d}}S'(\mathit{\boldsymbol{r}}, t) $
(5) 式中,积分的对象是一个半径为|r-r′|=ct的球形表面S′(r, t),在2维平面即断层平面,所有的光声信号源和测量点位于同一平面,此时积分是沿着半径为|r-r′|=ct的圆周L′(t)开展,忽略(5)式中的常数,光声断层成像的前向模型可表示为:
$ p(\mathit{\boldsymbol{r}}, t) = \frac{\partial }{{\partial t}}\int_{L'\left( t \right)} {\frac{{H\left( {\mathit{\boldsymbol{r'}}} \right)}}{{\left| {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r'}}} \right|}}} {\rm{d}}L'(t) $
(6) -
光声断层重建算法主要分为3种:第1种是基于雷登变换的滤波反投影重建算法; 第2种是基于时间反转方法的重建算法; 第3种是基于模型的重建算法。滤波反投影算法虽然实现容易且重建速度很快,但是其重建图像含有条状伪影而影响图像质量。时间反转方法虽然通过反向模拟超声波传播来得到更好质量的重建图像,但是这个过程需要复杂的数值仿真,不适合实时成像的要求。而基于模型的重建算法是在采集的声压信号数据和组织的吸收分布之间建立一种线性映射关系,继而通过最优化方法去最小化采集的声压信号与利用模型计算的声压信号之间的误差。因而具有很强的灵活性,且模型矩阵只与所使用的图像网格和信号采集系统的参量有关,而与实际的成像对象无关。
在基于模型的光声断层重建算法中,第1步是计算模型矩阵,需要用到导数的数值近似表示,因此(6)式可近似表示为:
$ p(\mathit{\boldsymbol{r}}, t) \approx \frac{{I\left( {\mathit{\boldsymbol{r}}, t\Delta t} \right) - I\left( {\mathit{\boldsymbol{r}}, t - \Delta t} \right)}}{{2\Delta t}} $
(7) 式中, 采用的是导数的中间差分近似。I(r, t)为:
$ I\left( {\mathit{\boldsymbol{r}}, t\Delta t} \right) = \int_{L'\left( t \right)} {\frac{{H\left( {\mathit{\boldsymbol{r'}}} \right)}}{{\left| {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{r'}}} \right|}}} {\rm{d}}L'(t) $
(8) 第2步就是计算(8)式,方法有很多[24-25]。最后(8)式和(9)式可以表示为:
$ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{Ax}} $
(9) 式中,p∈Rm为向量化表示的超声换能器阵元采集到的声压信号, x∈Rn为向量化表示的吸收分布,也即初始声压分布,A∈Rm×n是模型矩阵或系统矩阵,表示一个线性算子描述组织的光学吸收分布与换能器探测的声压信号数据之间的关系。
基于模型的重建算法可以分为两类,第1类是通过求解(10)式最小二乘问题的算法,成为朴素算法,其解称为朴素解:
$ {\mathit{\boldsymbol{x}}_{{\rm{native}}}} = \mathop {{\rm{argmin}}}\limits_x \left\| {\mathit{\boldsymbol{p}} - \mathit{\boldsymbol{Ax}}} \right\|_2^2 $
(10) 式中,xnaive为最终求解的朴素解。
第2类算法为基于正则化的算法,由于基于模型的光声断层图像重建问题通常是病态的,因此朴素解与精确解之间通常有较大的偏离,为了获得更好的近似解,需要使用各种正则化项,比如Tikhonov正则化、稀疏正则化、全变分正则化等。
-
整个系统的硬件组成示意图如图 1所示。光声断层成像系统的激发脉冲激光器采用的是德国INNOLAS公司生产的掺钕钇铝石榴石(Nd: YAG)激光器,该激光器分成两部分:前部分为抽运源,抽运波长为532nm,输出能量为400mJ,重复频率为10Hz,脉冲宽度为4ns~8ns; 后部分为光学参量振荡器(optical parametric oscillator, OPO)可调谐激光器,波长调谐范围为680nm~960nm的红光及近红光波段,在750nm时,输出能量超过80mJ。其余还有耦合透镜、耦合光纤和10根光线束。
超声换能器采集硬件局部放大图如图 2a所示。超声换能器采用的是法国IMASONIC公司的定制中心频率是5MHz,带宽为80%,覆盖角度为270°的128阵元弧形聚焦换能器,结构图如图 2b所示,每个阵元的结构图如图 3a所示。聚焦的半径为40mm,阵元的高度为15mm,相邻阵元之间的间隔为0.1mm。在成像水箱中,通过一个具有四肢的夹具把换能器夹住,使之水平放置。而换能器夹具的上下面各有5个可以放置耦合光纤端头的楔形槽,上面5个楔形槽均匀分割整个圆周,下面的5个楔形槽与上面相应位置的楔形槽堆成,且每个楔形槽与水平放置的换能器成一定角度,而每一个耦合光纤端头把耦合进来的激光整形为线光源,这样就把线光源均匀地照射到换能器的聚焦平面内。
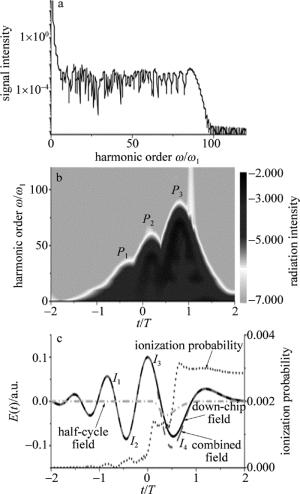
Figure 3. Schematic of transducer element and simulated cross-sectional view of spatial response for the transducer
如图 2a所示,成像小鼠通过悬挂臂支撑系统垂直固定,在实际在体的成像试验中,小鼠先涂上超声耦合胶,之后体表面覆盖一层薄膜与水隔离,最后在小鼠嘴部通过麻醉系统设置好麻醉。竖直的悬挂臂被固定在水平横梁上,而水平横梁与机械垂直升降台融为一体通过直线电机如图 1所示。这里采用直线电机是为了减少电磁干扰对采集系统的噪声影响。之后机械垂直升降台通过直线电机的上下运动来达到控制成像小鼠采集不同的断层切片。图 3b中描绘了此超声换能器仿真的声场图。可以看到, 成像平面是一个直径近似为20mm、厚度为0.7mm的圆盘,此圆盘切片保证了系统在进行断层成像时的特异性。
超声换能器采集的128通道超声信号通过基于NI的采集模块进行处理。具体是工控机机箱采用的是NI的配有8个插槽和高带宽背板的PXIe-1082,每个插槽都可以插入PXI Express模块,且含有一个系统定时同步插槽。主机采用的是NI的基于Intel core i7-3610QE处理器的高性能嵌入式控制器PXIe-8135, 负责协调整个采集过程,这样就不用在需要额外的计算机。定时和同步模块采用的是NI的PXIe-6674T, 用于同步脉冲激光器触发信号和多通道采集模块。采集处理模块采用的是NI FlexRIO硬件,其为NI LabVIEW现场可编程门阵列(field-programmable gate array, FPGA)提供灵活且可定制的I/O。此硬件包含两部分,分别是4个FPGA模块PXIe-7965R和4个提供高性能模拟和数字I/O的适配器模块NI 5752。NI 5752为32通道数字化适配器模块,分辨率为12位,采样频率为50MS/s,另外还含有抗混叠滤波器和可编程时变增益控制,这样就可以在模数转换过程中对微弱的光声信号进行高频滤波和增益放大,以增大信号的信噪比。这两部硬件共同构成一个可重新配置的子系统,通过LabVIEW FPGA软件进行编程。
-
整个采集系统的软件流程图如图 4所示。
首先, 脉冲激光器的同步触发信号给到PXIe-6674T,之后同步FlexRIO硬件采集数据,每个通道采集的数据会以一个一个64位的先进先出(first-in and first-out, FIFO)的数据结构通过直接内存访问(direct memory access, DMA)传输到内存,不需要经过控制器干预,然后再对数据进行处理,处理的数据可以一边进行实时显示,一边存储到硬盘进行后期重建。采集系统的前面板界面如图 5所示。
-
为了对整个光声断层成像系统进行验证,首先进行了系统的空间分辨率验证实验。利用水笔芯进行成像,水笔芯的内壁厚度为90mm,图 6a为成像结果图中通过水笔芯圆心的整个水平像素点特性曲线,图 6b为第2个峰值信号的局部放大图。在该峰值的一半处宽度测量为200μm,根据参考文献[26]中所述方法,一般来说,成像对象的大小近似为该物体真实大小和系统空间分辨率大小的平方和的平方根,即2002=902+r2,其中r为空间分辨率,所以该系统的空间分辨率约为180μm。
之后进行了离体成像实验。离体的实验对象是一个柱状模拟样品,用5%的琼脂粉和80%的去离子水经过搅拌均匀加热到透明状的液体后,再冷却到常温后加入15%的脂肪乳搅拌均匀,之后取一柱状容器,容器内固定两个六边形柱体模具,间隔为5mm,最后把混合液倒入容器内凝固形成一含有两个六边形柱体模具空腔的模拟样品仿体,再在空腔内注射黑色墨水,进行断层成像。激发波长为750nm,每次断层采集平均20次用于对原始数据进行去噪,一次采集长度为2600个点,图 7a为超声换能器第1个阵元采集的原始光声信号曲线。可以看到, 除有效信号外,噪声的幅值很小,这也说明了该光声断层成像采集系统具有很好的噪音抑制能力。重建算法采用的是正则化优化的基于模型的光声重建算法,结果图如图 7b所示。图像像素个数为256×256,每个像素的大小为0.1mm。可以看出, 重建结果中断层截面上两个六边形非常清楚。
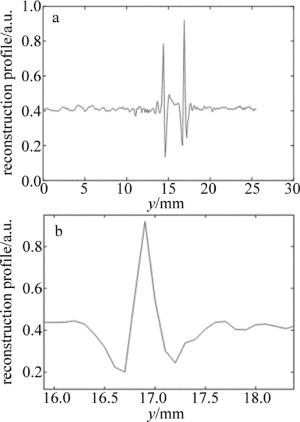
Figure 6. a—characteristic curve of horizontal pixel point in the reconstruction result of pen core b—partial enlargement of the second peak signals of Fig. 6a
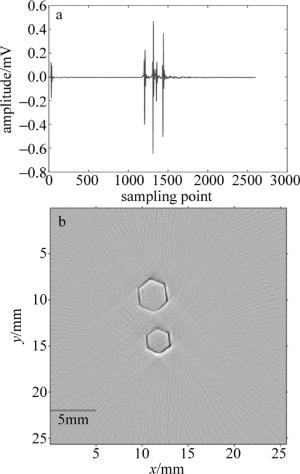
Figure 7. a—signal plot of 1# transducer b—the reconstructed photoacoustic tomography image of two hexagonal prisms
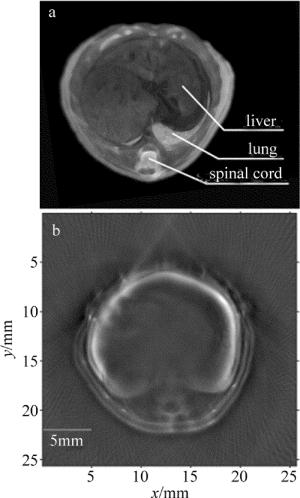
最终成像系统是为了能够开展小动物在体实验,所以又进行了在体小动物成像实验。实验对象为6周的BALB/c雄性裸鼠,在裸鼠体表涂上超声耦合胶用来保证声速的匹配,之后通过薄膜包裹保证实验中与水隔离。再把裸鼠嘴部接入异氟烷和氧气混合的麻醉气体,最后固定在小鼠固定支架上,激发波长为750nm,采集点数和采集平均次数分别为20和2600。通过控制直线电机的运动来采集裸鼠不同的断层数据。重建算法采用的是正则化优化的基于模型的光声重建算法,结果图如图 8b所示。可以看到,小鼠的肝部和脊柱都非常清晰,且重建图像内部非常均匀,伪影很少,另外裸鼠的皮肤与内脏的边界也很清晰,图 8a是裸鼠在该成像位置对应的组织切片图。重建图像的结果与组织切片图很吻合。图像像素个数为256×256,每个像素的大小为0.1mm。该试验很好地验证了该断层成像系统可以用来开展在体的小动物光声断层成像研究。
-
模拟样品和小鼠在体的成像实验结果均表明, 该断层成像系统可以用于开展小动物光声断层成像实验研究。另外该断层成像系统在采集一个断层数据且采集平均次数为20次时所耗费的时间为1.04ms,正则化优化的基于模型的光声重建算法在重建一个断层的数据且重建图像像素个数为256×256时所消耗的时间为40s左右,其中30s为系统矩阵的计算,剩余10s为重建图像的迭代计算。所以该断层成像系统可以高速采集断层数据,近实时地进行高质量的图像重建。后期计划对算法进行图形处理器加速以进一步缩短重建时间,使之达到实时。另外由于脉冲激光器为可调谐激光器,波长在红光和近红外波段连续可变,所以还可以进行多光谱成像,进而对组织中的血红蛋白和光声造影剂进行光谱分离,以提升该系统的科研应用价值。
高速128通道小动物多光谱光声断层成像系统
High-speed and 128-channel multi-spectral photoacoustic tomography system for small animal
-
摘要: 为了实现小动物光声断层信号的高速采集和实时高质量图像的重建,采用了覆盖角度为270°的128阵元弧形聚焦超声换能器、4个32通道的NI公司数据采集模块和可调谐脉冲激光器以及正则化优化的基于模型的光声断层重建算法。结果表明,系统的空间分辨率可以达到180μm;此系统可以在1ms内完成光声断层数据的采集,在40s以内获得高质量的重建图像。该系统可以用于开展小动物在体的多光谱光声断层成像实验研究。Abstract: In order to achieve high-speed acquisition and real-time high-quality image reconstruction of photoacoustic tomography signals for small animal, a 128 element arc-shaped focused ultrasound transducer with 270° coverage angle, four 32 channel NI data acquisition modules, a tunable pulsed laser and model-based photoacoustic tomography reconstruction algorithm with regularized optimization were used. The spatial resolution of the system can be up to 180μm. The in vitro and in vivo imaging experiments show that the system can complete photoacoustic tomography data acquisition within 1ms, and obtain high quality reconstructed images within 40s. The system can be used to carry out in vivo multi-spectral photoacoustic tomography of small animals.
-
Figure 6. a—characteristic curve of horizontal pixel point in the reconstruction result of pen core b—partial enlargement of the second peak signals of Fig. 6a
-
[1] KARABUTOV A, SAVATEEVA E, ORAEVSKY A. Optoacoustic tomography:New modality of laser di agnostic systems[J]. Laser Physics, 2003, 13(5):711-723. [2] WANG L V, HU S. Photoacoustic tomography:in vivo imaging from organelles to organs[J]. Science, 2012, 335(6705):1458-1462. [3] WANG X, PANG Y, KU G, et al. Noninvasive laser-induced photoacoustic tomography for structural and functional in vivo imaging of the brain[J]. Nature Biotechnology, 2003, 21(7):803-806. doi: 10.1038/nbt839 [4] LI C, WANG L V. Photoacoustic tomography and sensing in biomedicine[J]. Physics in Medicine and Biology, 2009, 54(19):R59-R97. doi: 10.1088/0031-9155/54/19/R01 [5] WANG L V. Prospects of photoacoustic tomography[J].Medical Physics, 2008, 35(12):5758-5767. doi: 10.1118/1.3013698 [6] NTZIACHRISTOS V, RAZANSKY D. Molecular imaging by means of multispectral optoacoustic tomography (MSOT)[J]. Chemical Reviews, 2010, 110(5):2783-2794. doi: 10.1021/cr9002566 [7] KOLKMAN R G M, BRANDS P J, STEENBERGEN W, et al. Real-time in vivo photoacoustic and ultrasound imaging[J]. Journal of Biomedical Optics, 2008, 13(5):050510. doi: 10.1117/1.3005421 [8] NIEDERHAUSER J J, JAEGER M, LEMOR R, et al. Combined ultrasound and optoacoustic system for real-time high-contrast vascular imaging in vivo[J]. IEEE Transactions on Medical Imaging, 2005, 24(4):436-440. doi: 10.1109/TMI.2004.843199 [9] OLAFSSON R, BAUER D R, MONTILLA L G, et al. Real-time, contrast enhanced photoacoustic imaging of cancer in a mouse window chamber[J]. Optics Express, 2010, 18(18):18625-18632. doi: 10.1364/OE.18.018625 [10] XU D, LIANG Zh X, JI X. Photoacoustic imaging system based on multi-channel parallel acquisition[J]. Chinese Journal of Lasers, 2011, 38(2):0204002(in Chinese). doi: 10.3788/CJL [11] XIANG L, WANG B, JI L, et al. 4-D photoacoustic tomography[J]. Scientific Reports, 2013, 3:1113. doi: 10.1038/srep01113 [12] TAN Y, HE J F, REN Y J, et al. Fast photoacoustic imaging systems based on rotating multi-element linear transducer array[J]. Laser Technology, 2009, 33(5):300-302(in Chinese). [13] CHEN Z, TANG Z, WAN W. Photoacoustic tomography imaging based on a 4f acoustic lens imaging system[J]. Optics Express, 2007, 15(8):4966-4976. doi: 10.1364/OE.15.004966 [14] KOZHUSHKO V, KHOKHLOVA T, ZHARINOV A, et al. Focused array transducer for two-dimensional optoacoustic tomography[J]. The Journal of the Acoustical Society of America, 2004, 116(3):1498-1506. doi: 10.1121/1.1781710 [15] KRUGER R A, KISER W L, Jr, REINECKE D R, et al. Thermoacoustic computed tomography using a conventional linear transducer array[J]. Medical Physics, 2003, 30(5):856-860. doi: 10.1118/1.1565340 [16] PARK S, MALLIDI S, KARPIOUK A B, et al. Photoacoustic imaging using array transducer[C]//International Society for Optics and Photonics. San Jose, USA: SPIE, 2007: 643714. [17] YIN B, XING D, WANG Y, et al. Fast photoacoustic imaging system based on 320-element linear transducer array[J]. Physics in Medicine and Biology, 2004, 49(7):1339-1346. doi: 10.1088/0031-9155/49/7/019 [18] ZEMP R J, BITTON R, LI M L, et al. Photoacoustic imaging of the microvasculature with a high-frequency ultrasound array transducer[J]. Journal of Biomedical Optics, 2007, 12(1):010501. doi: 10.1117/1.2709850 [19] KRUGER R A, KISER W L, REINECKE D R, et al. Thermoacoustic molecular imaging of small animals[J]. Molecular Imaging, 2003, 2(2):113-123. doi: 10.1162/153535003322331993 [20] GAMELIN J, AGUIRRE A, MAURUDIS A, et al. Curved array photoacoustic tomographic system for small animal imaging[J]. Journal of Biomedical Optics, 2008, 13(2):024007. doi: 10.1117/1.2907157 [21] YANG S, XING D, ZHOU Q, et al. Functional imaging of cerebrovascular activities in small animals using high-resolution photoacoustic tomography[J]. Medical Physics, 2007, 34(8):3294-3301. doi: 10.1118/1.2757088 [22] COX B T, KARA S, ARRIDGE S R, et al. k-space propagation models for acoustically heterogeneous media:Application to biomedical photoacoustics[J]. The Journal of the Acoustical Society of America, 2007, 121(6):3453-3464. doi: 10.1121/1.2717409 [23] DEAN-Ben X L, BUEHLER A, NTZIACHRISTOS V, et al. Accurate model-based reconstruction algorithm for three-dimensional optoacoustic tomography[J]. IEEE Transactions on Medical Imaging, 2012, 31(10):1922-1928. doi: 10.1109/TMI.2012.2208471 [24] DEAN-BEN X L, NTZIACHRISTOS V, RAZANSKY D. Acceleration of optoacoustic model-based reconstruction using angular image discretization[J]. IEEE Transactions on Medical Imaging, 2012, 31(5):1154-1162. doi: 10.1109/TMI.2012.2187460 [25] LIU H, WANG K, PENG D, et al. Curve-driven-based acoustic inversion for photoacoustic tomography[J]. IEEE Transactions on Medical Imaging, 2016, 35(12):2546-2557. doi: 10.1109/TMI.2016.2584120 [26] ZENG L, XING D, GU H, et al. High antinoise photoacoustic tomography based on a modified filtered backprojection algorithm with combination wavelet[J]. Medical Physics, 2007, 34(2):556-563. doi: 10.1118/1.2426406 -


 网站地图
网站地图

 下载:
下载: