-
激光因其具有亮度高、相干性强以及单色性好等优良特性,被广泛应用于众多领域[1-2]。但是激光器发射出的激光光束都会有一定的发散角,当把激光应用到激光雷达、激光测距和激光通信等领域时,由于这些领域都需要激光进行远距离传输,所以激光发散角过大时会造成无法直接应用。在实际应用中,为了实现远距离传输激光,需要采用倒置的望远光学系统对激光进行扩束,压缩激光的发散角。通常把这种利用倒置望远光学系统对激光光束发散角进行压缩的技术称之为激光发射天线技术。为了满足不同的应用要求,可以通过设置不同的倒置望远光学系统透镜组合方式来改变激光发散角的压缩比,进而得到具有不同尺寸的激光光束[3-15]。
作者设计的激光发射天线仿真平台以倒置望远光学系统为激光发射天线的基本结构,借助MATLAB仿真软件强大的数值计算和图形显示功能,对激光经过激光发射天线前后的激光光斑2维、3维光强分布、3维结构激光光束以及激光天线变换后激光束腰与透镜组合离焦量之间的关系曲线进行仿真,在MATLAB GUI中通过灵活设置激光谐振腔关键结构参量以及倒置望远镜系统的透镜组合方式来得到具有不同发散角的激光光束,为工程设计中激光发射天线结构优化设计提供新的可视化自动设计手段[16-20]。
-
任何结构的稳定谐振腔所生成的沿着z轴方向进行传播的基模高斯光束,其空间任意位置光场强度E00(x, y, z)均可由如下的一般形式表示[1-2]:
$ \begin{array}{l} {E_{00}}\left( {x, y, z} \right) = \frac{a}{{w\left( z \right)}}\exp \left[{-\frac{{{r^2}}}{{{w^2}\left( z \right)}}} \right] \times \\ \exp \left\{ { - {\rm{i}}\left[{k\left( {z + \frac{{{r^2}}}{{2R\left( z \right)}}} \right)-\arctan \left( {\frac{z}{f}} \right)} \right]} \right\} \end{array} $
(1) $ w\left( z \right) = {w_0}\sqrt {1 + {{\left( {\frac{z}{f}} \right)}^2}} $
(2) $ R\left( z \right) = z\left[{1 + {{\left( {\frac{f}{z}} \right)}^2}} \right] = z + \frac{{{f^2}}}{z} $
(3) $ f = \frac{{\pi w_0^2}}{\lambda } $
(4) 式中, λ为激光波长; k为波数; a为常数因子; w0为基模高斯光束的束腰半径; w(z)为与激光传播轴线相交于z点的基模高斯光束等相位面上的光斑半径; f为基模高斯光束的共焦参量; R(z)为与激光传播轴线相交于z点的基模高斯光束等相位面的曲率半径; r是传播轴不同位置光斑上的不同点与光轴之间的距离。根据(1)式可以得出,通过基模高斯光束的参量f(或w0)可以描述其具体波形,这就使作者能够深入研究基模高斯光束本身的特性以及传播规律,而不用考虑它是由何种几何结构的稳定谐振腔所产生的。
根据(2)式,基模高斯光束的远场发散角可表示为:
$ {\theta _0} = \mathop {\lim }\limits_{z \to \infty } \frac{{2w\left( z \right)}}{z} = 2\frac{\lambda }{{\pi {w_0}}} $
(5) 从(5)式可得出,束腰半径越大,高斯光束的远场发散角越小,反之,远场发散角越大。激光发散角压缩的过程,也可看成是激光束腰变大,激光扩束的过程。
对于由一般稳定球面谐振腔所生成的基模高斯光束,其参量f以及w0与谐振腔结构参量R1, R2, L之间的关系为:
$ w_0^4 = {\left( {\frac{\lambda }{\pi }} \right)^2}\frac{{L\left( {{R_1}-L} \right)\left( {{R_2}-L} \right)\left( {{R_1} + {R_2}-L} \right)}}{{{{\left( {{R_1} + {R_2} - 2L} \right)}^2}}} $
(6) $ {f^2} = \frac{{L\left( {{R_1}-L} \right)\left( {{R_2}-L} \right)\left( {{R_1} + {R_2}-L} \right)}}{{{{\left( {{R_1} + {R_2} - 2L} \right)}^2}}} $
(7) 式中, R1和R2分别为激光谐振腔两侧的曲率半径,L为激光谐振腔腔长。
-
根据(5)式以及高斯光束束腰变换公式,高斯光束通过焦距为F的透镜后,其高斯光束的发散角为[1]:
$ {\theta _0}^\prime = \frac{{2\lambda }}{\pi }\sqrt {\frac{1}{{w_0^2}}{{\left( {1-\frac{l}{F}} \right)}^2} + \frac{1}{{{F^2}}}{{\left( {\frac{{\pi {w_0}}}{\lambda }} \right)}^2}} $
(8) 式中, l为激光变换前束腰与透镜的距离。从式中可看出,无论F和l取什么数值,都不可能使θ0′→0,所以采用单一透镜使高斯光束变为平面波,在理论上是不可能实现的。根据(5)式,要想用透镜来压缩高斯光束的发散角,当w0′>w0时,将有θ0′ < θ0,所以在一定条件下,当w0′达到极大值时,θ0′达到极小值。
根据(8)式,当l=F时,θ0′达到极小值:
$ {\theta _0}^\prime = 2\frac{\lambda }{{\pi {w_0}^\prime }} = 2\frac{{{w_0}}}{F} $
(9) 可见,当透镜焦距F一定时,若l=F,θ0′将达到极小值,而F越大,θ0′越小。根据此结论可得,单透镜准直效果只与透镜焦距这一因素有关,并不能充分利用w0这一影响最终准直效果的重要因素,其准直能力有限。
-
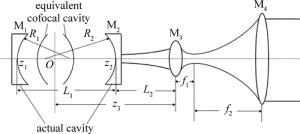
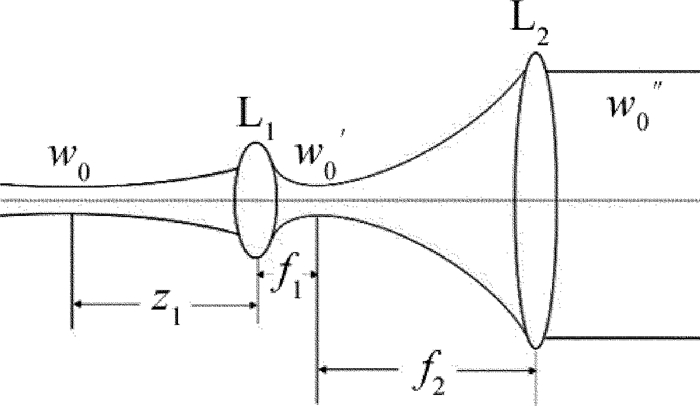
激光发射天线常采用倒置的望远光学系统作为其基本结构,如图 1所示。透镜L1为焦距为f1的短焦距凸透镜(称为副镜或者物镜),入射激光光束经凸透镜L1变换后其束腰半径由w0缩小到w0′; 透镜L2为焦距为f2的长焦距凸透镜(称为目镜,或者主镜),其焦点所在位置正好与入射激光光束经凸透镜L1变换后的束腰半径w0′所在位置重合,最后从凸透镜L2出射的激光光束束腰半径为w0″。两凸透镜焦距f1 < f2,两透镜之间的距离为f1+f2,副镜L1与激光天线变换前的激光束腰所在位置之间的距离为z1,此时经过副镜L1变换后的激光束腰半径可表示为:
$ {w_0}^\prime = \frac{{{w_0}{f_1}}}{{\sqrt {{{\left( {{f_1}-{z_1}} \right)}^2} + \frac{{{\pi ^2}w_0^4}}{{{\lambda ^2}}}} }} $
(10) 在${z_1} \gg {f_1}$的条件下,副镜L1将波长为λ的激光光束聚焦到主镜L2的前焦面上,此时就得到了一个极小的光斑:
$ {w_0}^\prime = \frac{{\lambda {f_1}}}{{\pi w\left( {{z_1}} \right)}} $
(11) 聚焦到主镜L2的前焦面上激光光束再经过透镜L2变换后,激光束腰半径w0″达到极大值:
$ {w_0}^{\prime \prime } = \frac{\lambda }{{\pi {w_0}^\prime }}{f_2} $
(12) 此时高斯光束经过激光发射天线后的发散角:
$ {\theta _0}^{\prime \prime } = 2\frac{\lambda }{{\pi {w_0}^{\prime \prime }}} = 2\frac{{\lambda {f_1}}}{{\pi {f_2}w\left( {{z_1}} \right)}} $
(13) (11) 式中的w(z1)为入射在副镜L1表面上的激光光斑半径。经过短焦距透镜L1变换后的激光束腰正好落在长焦距透镜L2的前焦面上,同时获得一个半径极小的光斑,然后在经过一个长焦距透镜的变换,由(12)式以及(13)式可得束腰半径为w0的高斯光束, 经过激光发射天线后就可获得一个很好的准直效果,其激光发散角被很好的压缩,所以选用图 1中的透镜组合作为激光发射天线的基本结构。
-
此激光发射天线仿真平台的仿真设计以图 2中的结构模型作为基本仿真模型。此仿真模型主要包括两种结构,分别是生成激光的激光谐振腔以及激光发射天线基本结构。其中产生激光的稳定谐振腔两个反射镜M1和M2的曲率半径分别为R1和R2,稳定谐振腔的腔长为L1,激光发射天线的副镜M3焦距为f1,主镜M4的焦距为f2,激光天线副镜M3与稳定谐振腔反射镜M2的距离为L2。采用谐振腔的3个结构参量R1, R2, L1,根据激光束腰半径计算(9)式计算出稳定谐振腔生成的激光束腰半径大小,然后根据束腰半径w0这一重要参量可进行接下来的高斯光束仿真。
当谐振腔的3个结构参量R1, R2, L1满足稳定性条件时,与其等价的共焦谐振腔就可以唯一的确定下来。等价共焦谐振腔的位置的确定采用如下公式:
$ \left\{ \begin{array}{l} {z_1} = \frac{{{L_1}\left( {{R_2}-{L_1}} \right)}}{{\left( {{L_1}-{R_1}} \right) + \left( {{L_1}-{R_2}} \right)}}\\ {z_2} = \frac{{ - {L_1}\left( {{R_1} - {L_1}} \right)}}{{\left( {{L_1} - {R_1}} \right) + \left( {{L_1} - {R_2}} \right)}} \end{array} \right. $
(14) 式中, z1,z2分别为反射镜M1,M2与等价共焦谐振腔中心的距离,也就是与生成的激光光束束腰之间的距离(距离为负时,在束腰左侧; 距离为正时,在束腰右侧),然后根据激光天线副镜M3与谐振腔反射镜M2的距离为L2就可以计算出激光天线副镜M3与谐振腔生成的激光高斯光束束腰之间的距离z3,这样就为激光光束的仿真提供了重要参量。
-
设计的激光发射天线仿真平台的主要功能是通过激光仿真来分析基模高斯光束经过激光发射天线前后激光束腰位置处光斑2维光强分布、激光束腰位置处的光斑3维光强分布、激光3维光束结构以及激光天线变换后激光束腰与透镜组合离焦量之间的关系曲线的变化。用MATLAB GUI设计的激光发射天线仿真平台设计的步骤为:(1)设计用户界面上各控件的布局分布, 其中主要包括实验参量的构成、仿真结构模型图在用户界面上的显示以及仿真触发按钮(simulation(A)按钮代表的是激光束腰原2维光强分布,simulation(B)按钮代表的是激光经过激光发射天线发射后的束腰2维光强分布,simulation(C)按钮代表的是激光束腰原3维光强分布, simulation(D)按钮代表的是激光经过激光发射天线发射后的3维光强分布, simu-lation(E)按钮代表的是激光原3维光束, simulation(F)激光经过激光发射天线发射后的光束3维结构, simulation(G)按钮代表的是变换后激光束腰与透镜组合离焦量的关系曲线)的组成; (2)合理设置各个控件颜色、大小、文字等属性,设计好的用户界面如图 3所示; (3)设计编写初始界面函数(Opening Fcn)和控件的回调函数(Callback)的代码。
-
回调函数代码是整个仿真设计中的关键,是对界面控件触发时的事件响应函数。各仿真按钮主要回调函数的设计编写流程如下。
-
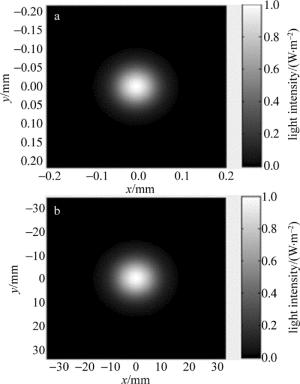
(1) 在GUI的图形用户界面中输入各个参量; (2)根据(6)式推导激光谐振腔的出射激光光束束腰半径; (3)根据(14)式计算出激光谐振腔的等价共焦谐振腔位置; (4)计算出激光天线副镜M3与谐振腔生成的激光高斯光束束腰的距离z3; (5)由(11)式计算高斯光束经过透镜M3后的束腰半径; (6)根据(12)式计算高斯光束经过透镜M4后的束腰半径; (7)计算经过激光发射天线变换后沿z轴传输的激光束腰位置处x-y平面内不同采样点的归一化光强值I; (8)MATLAB中用imagesc(x, y, I, [0 1])函数仿真出经过激光发射天线变换后激光束腰位置处光斑的2维光强分布。
-
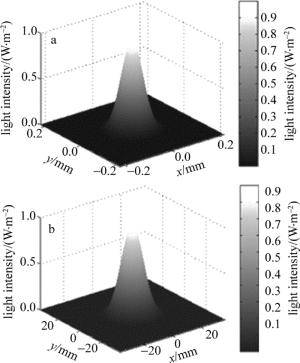
(1) 在GUI的图形用户界面中输入各个参量; (2)根据(6)式推导激光谐振腔的出射激光束腰半径; (3)根据(14)式计算出激光谐振腔的等价共焦谐振腔位置; (4)计算出激光天线副镜M3与谐振腔生成的激光高斯光束束腰的距离z3; (5)根据(11)式计算高斯光束经过透镜M3后的束腰半径; (6)根据(12)式计算高斯光束经过透镜M4后的束腰半径; (7)计算激光天线变换后沿z轴传输的激光束腰位置处x-y平面内不同采样点的归一化光强I; (8)在MATLAB中用surf(x, y, I)函数仿真出激光天线变换后激光束腰位置处光斑的3维光强分布。
-
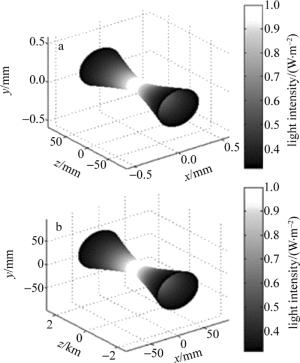
(1) 在GUI的图形用户界面中输入各个参量; (2)根据(6)式推导激光谐振腔的出射激光光束束腰半径; (3)根据(14)式计算出激光谐振腔的等价共焦谐振腔位置; (4)计算出激光天线副镜与谐振腔生成的激光高斯光束束腰的距离; (5)计算高斯光束经副镜M3后的束腰半径; (6)计算高斯光束经透镜M4后的束腰半径; (7)计算出激光天线变换后的沿着z轴传输的激光在特定z位置处的光斑半径w(z); (8)根据两个变量z和θ,求出了3维高斯光束曲面各点X,Y,Z 3个坐标的极坐标表达式:
$ \left\{ \begin{array}{l} X = w\left( z \right)\cos \theta, \left( {0 \le \theta \le 2\pi, -\infty \le z \le \infty } \right)\\ Y = w\left( z \right)\sin \theta, \left( {0 \le \theta \le 2\pi, -\infty \le z \le \infty } \right)\\ Z = z, \left( {-\infty \le z \le \infty } \right) \end{array} \right. $
(15) (9) 在MATLAB中用mesh(w(z)cosθ, w(z)sinθ, z)函数仿真出激光天线变换后的激光3维高斯光束曲面。
-
(1) 在GUI的图形用户界面中输入各个参量; (2)根据(6)式推导激光谐振腔的出射激光光束束腰半径; (3)根据(14)式计算出激光谐振腔的等价共焦谐振腔位置; (4)计算出激光天线副镜与谐振腔生成的激光高斯光束束腰的距离; (5)计算高斯光束经副镜M3后的束腰半径; (6)计算高斯光束经副镜M3后的束腰所在位置; (7)把透镜组合离焦量变量(主镜M4焦点在副镜M3焦点左侧时离焦量为负,在右侧时离焦量为正)引入高斯光束经透镜M4后的束腰半径计算过程; (8)用plot(x, y)函数绘制激光天线变换后激光束腰与透镜组合离焦量之间的关系曲线。
-
在MATLAB GUI图形用户界面中输入各参量,激光谐振腔结构参量腔长L1=300mm,R1=2000mm,R2=2000mm,激光波长为550nm,激光发射天线透镜副镜M3焦距f1=15mm,主镜M4焦距f2=120mm,副镜M3与激光谐振腔M2镜之间的距离L2=500mm。在此参量条件下激光谐振腔生成的激光经过此激光发射天线前后的仿真结果如下。
图 4~图 7分别为经激光发射天线变换后基模高斯光束束腰光斑2维光强分布、束腰3维光强分布、3维光束曲面仿真结果以及激光天线变换后激光束腰与透镜组合离焦量之间的关系曲线的仿真图。从中可以看出,在此参量条件下,通过对激光发射天线变换前后仿真结果的对比分析,可以在此参量输入条件下激光谐振腔出射的激光经过激光天线变换后束腰半径从0.073mm变成了12.202mm,激光发散角从0.275°变为0.00164°,成功实现了激光扩束,大大减小了激光发散角。从激光束腰与透镜组合离焦量之间的关系曲线可看出,由于谐振腔与激光发射天线副镜之间距离并不是无限远,激光经过激光发射天线副镜变换后,其束腰并不是准确落到副镜右焦点位置,所以激光天线变换后束腰半径最大的位置并不是镜头离焦量为0mm的位置,而是向右平移了大约0.37mm。以上仿真结果与激光发射天线理论计算值相符,满足了激光天线的设计使用要求。
-
此激光发射天线仿真平台利用平台仿真软件成功实现了对激光基模高斯光束经过激光发射天线前后的激光光束束腰光斑2维光强分布、束腰3维光强分布、3维结构激光光束以及激光束腰与透镜组合离焦量之间的关系曲线的仿真模拟。通过在MATLAB GUI用户交互界面中修改变动相关实验参量,仿真出了不同条件下的实验现象和结果,为激光发射天线的优化设计提供了一种新的可视化自动设计方法。
激光发射天线仿真平台设计
Simulation design of laser transmitting telescope
-
摘要: 为了给激光发射天线的设计优化提供一种可视化自动设计手段,采用MATLAB仿真技术构建了一种基于倒置望远镜系统结构的激光发射天线仿真平台, 进行了激光发射天线的理论分析和仿真实验验证。通过灵活设置激光谐振腔关键结构参量以及倒置望远镜系统透镜组合方式,实现了发射天线发射前后的激光2维光强分布、激光3维光强分布、激光光束3维结构以及变换后激光束腰与透镜组合离焦量的关系曲线的仿真。结果表明,波长550nm的激光变换后束腰半径从0.073mm变为12.202mm,发散角从0.275°变为0.00164°,成功压缩了激光发散角; 此平台进行的仿真过程形象直观,可根据需要自动优化设计出最优的激光发射天线结构。该仿真平台的构建为激光发射天线的可视化自动设计提供了全新的方法。Abstract: In order to provide a visual automatic design method for the design optimization of laser transmitting telescopes, by using Matlab simulation technology, A simulation platform of laser transmitting telescope based on an inverted telescope system structure was constructed. Theoretical analysis and experimental verification of the laser transmitting telescope were carried out. By setting the key structural parameters of the laser resonator and the lens combination of the inverted telescope system, 2-D laser intensity distribution, 3-D laser intensity distribution and 3-D structure of laser beam before and after launch were achieved. The relationship between laser beam waist and the defocus value of the combined lens was simulated. The results show that the waist radius is from 0.073nm to 12.202mm after laser transformation at wavelength of 550nm. The divergence angle changes from 0.275°to 0.00164°. Laser divergence angle is successfully compressed. The simulation process of the platform is visual and intuitive. The optimum structure of laser transmitting telescope can be automatically optimized according to the need. The simulation platform provides a new method for the automatic visual design of laser transmitting telescopes.
-
Key words:
- optical design /
- laser transmitting telescope /
- MATLAB /
- simulation
-
[1] ZHOU B K. The principle of laser [M]. Beijing: National Defense Industry Press, 2014: 67-81(in Chinese). [2] SUN H Y, ZHANG T H, HAN Y. Laser technology for military[M].Beijing: National Defense Industry Press, 2011: 1-21 (in Chinese). [3] CHENG J, SUN N C, WANG Zh X, et al. Maladjustment and beam expanded ratio of laser beam expanding telescope [J]. Laser Techno-logy, 1995, 19(1): 57-60 (in Chinese). [4] ZENG X D, YU Ch Q, ZHAN Y Sh. Collimation of semiconductor laser beams[J].Acta Photonica Sinica, 1999, 19(6): 295-298 (in Chinese). [5] QU W J. Optical experiment simulations with matlab [D].Xi'an: Northwestern Ploytechnical University, 2004: 5-16 (in Chinese). [6] LIU D Y, YI Sh H, GU J L. Principle of laser antenna design and light spot preservation with angular method [J]. Optics & Optoelectronic Technology, 2006, 4(2): 19-22(in Chinese). [7] GU J L, BI Ch N, YI Sh H. Laser antenna design by the angular control method [J]. Optical Technique, 2006, 32(s1): 148-150(in Chinese). [8] HAO P M, YUAN L Y, LI K X, et al. ∅300 Hartmann field flattening laser beam expander [J].Proceedings of the SPIE, 2007, 6722: 672206. doi: 10.1117/12.782673 [9] FAN L N, ZHU A M, LIU L, et al. Optical design of laser beam expanding telescope [J]. Infrared, 2007, 28(8):20-22 (in Chin-ese). [10] ZHENG P, YANG Y P, GAO H Y, et al. Design of two-level laser beam expander based on Galilean structure [J]. Journal of Applied Optic, 2008, 29(3): 347-350 (in Chinese). [11] GONG D, WANG H, TIAN T Y, et al. The optical design of high-power laser-beam expander [J]. Laser Technology, 2009, 33(4): 426-428(in Chinese). [12] WANG X J. Measurement and design of the beam expander as 60 micro-radiation antenna [J]. Acta Photonica Sinica, 2011, 40(s1): 73-76 (in Chinese). [13] KANG Z J, HAN X Y, LI C, et al. Analysis of the radio on free space optical transmission link for the satellite-to-ground communication [J]. Acta Optica Sinica, 2014, 34(10): 1001-1004. [14] ZHANG L. Novel structure design of laser-emitting antenna system and its transmission efficiency analysis [D]. Chengdu: University of Electronic Science and Technology of China, 2016: 9-18 (in Chin-ese). [15] LIU J Q, WANG N, YANG Y Y, et al. A micro acousto-optic Q-switched laser with narrow pluse width [J]. Laser Technology, 2017, 41(4): 562-565 (in Chinese). [16] DENG Ch R. Based on the MATLAB GUI multi-functional calculation system design and realization [D]. Nanchang: Nanchang University, 2012: 6-12 (in Chinese). [17] ZHANG W Sh, SHANG J F, LIU X L, et al. Design of wave optics simulation platform based on MATLAB GUI[J]. Physical Experiment of College, 2013, 26(3): 85-87 (in Chinese). [18] CHENG G F, WANG Sh, LI Q, et al. Simulation design of the laser destruction for CCD based on MATLAB[J]. Journal of Changchun University of Science and Technology, 2017, 40(6): 52-56 (in Chinese). [19] ZHANG Q G, LI Ch G, LOU Y L, et al. Amplitude optical pupil filters with power function distribution [J]. Laser Technology, 2017, 41(5): 743-748 (in Chinese). [20] SUN H, XU J M, ZHANG H Ch, et al. Simulation of three-junction GaAs solar cell temperature field by continuous wave laser irradiation [J]. Laser Technology, 2018, 42(2): 239-244 (in Chinese). -


 网站地图
网站地图

 下载:
下载: