-
木器漆是犯罪现场常见的微量物证之一,主要附着在作案工具和犯罪嫌疑人的衣服上,通过对木器漆的同一认定可确定犯罪嫌疑人是否出现在犯罪现场,为侦查活动提供线索和方向,为快速侦破刑事案件提供一种手段。木器漆主要分为水性木器漆[1-2]和溶剂型木器漆[3-4],水性木器漆的成分一般包含水、乳液、颜填料和各种助剂,溶剂型的成分一般包含树脂、颜填料、溶剂和各种助剂[5-6]等。水性木器漆具有低危害、低污染的环保特点;而溶剂型木器漆含苯,甲醛和二甲苯等对人体产生危害的物质[7]。随着人们生活质量的提高,水性木器漆因其绿色环保的优点被广泛使用,溶剂型木器漆逐渐退出市场。然而,在法庭科学领域,关于水性木器漆的研究相对较少,如何快速简单准确的对水性木器漆进行分析鉴别成为物证鉴定工作的重点之一。
傅里叶变换喇曼光谱仪的激发装置是长波近红外激光器,再用迈克尔逊干涉仪调制分光,将近红外激发喇曼技术与傅里叶变换技术相结合。与显微激光喇曼光谱易产生荧光效应不同,傅里叶变换喇曼光谱能有效抑制荧光效应,从而可对某些含荧光或对光不稳定的化合物进行分析,具有光谱范围宽、速度快、谱图重现性好和无损分析的特点[8-10],在激光应用[11-12]、化学[13-14]、生物医学[15-16]和高分子结构研究[17-18]等领域有广泛应用。BUZZINI等人[19]应用喇曼光谱结合多种激光波长对不同颜色的丙烯酸、棉和羊毛纺织纤维进行了有效区分。ZIEBA-PALUS等人[20]将喇曼光谱与红外光谱结合对刑事案件中出现的油漆进行分析,确定参与事故的车辆。WU等人[21]利用喇曼光谱对脐带血红细胞与先天性心脏病患者红细胞进行对比分析,结果表明, 两者喇曼光谱之间有较明显的特征差异,为提高新生胎儿先天性心脏病的检出率提供了技术支持。
本文中采集了3种品牌38个样品的光谱数据,通过数据的预处理,结合主成分分析对原始数据进行降维,再利用径向基函数将主成分分析后的主成分分数进行验证分析,选取准确率与召回率最优的维度建立分类模型,并对得到的模型结果进行讨论,以期为水性木器漆的快速有效鉴别提供一定的参考和借鉴。
-
本实验中选取了市场上常见的晨阳(CHENYANG, CY)、华彩士(HUACAISHI, HC)和雀尚(QUESHANG, QS)三大品牌, 其中晨阳样品12个,华彩士样品19个,雀尚样品7个,总共38个样本。表 1是从不同品牌随机抽取两个不同型号,共6个样本的基本信息。其它样本数据略。
Table 1. The details of 6 samples
number brand category manufacturer CY003 CHENYANG water-borne multifunctional paint CHENYANG CY005 CHENYANG water-borne multifunctional paint CHENYANG HC003 HUACAI water-based environmental protection paint CHAOMEIYAQI HC006 HUACAI water-based environmental protection paint CHAOMEIYAQI QS002 QUESHANG water-based anti-rust finish CHANGFENGHUANBAO QS009 QUESHANG waterborne furniture finish CHANGFENGHUANBAO -
主成分分析(pincipal component analysis, PCA)是一种有效的降维方法[22]。其基本思路是将高维度数据的特征映射到低维度上,且映射后的数据特征具有两两正交的特点,是从原有高维特征的基础上根据数据的特点重新构造出来的,所得到正交的低维特征就是主成分。PCA的工作原理就是在原始复杂的数据基础上,将方差最大的方向作为主成分分数的第1维,再以此维度垂直的平面上确定一个方差最大的方向作为第2维,第3维选择与前两维正交的平面中方差最大的坐标轴。同理,再经过多次重新选择,得到新的数据模型。在新的数据模型上发现,前k个方向上的累计方差无限接近100%,余下的方差和几乎为0。于是,对后面影响极小的特征忽略不计,只对前k维特征作为主成分进行保留。
径向基函数(radial basis function, RBF)是一个实值函数,它的值与到中心点的位移有关,一般RBF使用欧几里得度量及高斯函数,令μi为隐藏层中第i个节点的高斯函数中心点,取:
$ {\sigma _i} = {\frac{{\left\| {x - {\mu _i}} \right\|}}{{2{\sigma ^2}}}^2} $
(1) 式中, x为自变量,σ2为方差。
把(1)式代入高斯函数的公式,则有:
$ \varphi (\left\| {x - {\mu _i}} \right\|) = {\rm{exp}}( - {\frac{{\left\| {x - {\mu _i}} \right\|}}{{2{\sigma ^2}}}^2}{\rm{ }}) $
(2) RBF神经网络的基本思想是:将线性不可分的低维数据映射到高维空间中,得到的高维空间数据线性变得可分。在数据中找到能够代表整体数据的中心点,调整部分对输出具有重大影响的权重。径向基函数神经网络选择Z个隐藏层中的基函数, $ {x - {\mu _i}}$越小,输出值就越大。中心点矩阵,其中, m为隐层神经元数,n为输入层的神经元数。各个μi对应的σi使隐层中每个神经元最大程度地反映相应的不同输入信息。
最终的输出结果为:
$ \begin{array}{l} {y_j} = \sum\limits_{i = 1}^m {{w_{ij}}\varphi \left(|| {x-{\mu _i}||{^2}} \right), } \\ \;\;\;\;\;\;\;(j = 1, 2, \ldots , P;P<n) \end{array} $
(3) -
实验中采集的原始光谱数据存在维度较高、部分数据异常(偏离期望值)。为提升数据处理的速度并得到更加容易理解的结果,采用PCA对原始数据进行分析,对高维数据中的重要特征进行保留,降低变量的维度,削弱部分异常数据和噪声的干扰,实现对数据深度挖掘的目的。分析得到38个样品的主成分特征根方差贡献率。
在主成分分析中,一般把特征根大于1,累计方差贡献率大于85%的作为原始变量的主成分分数,特征根是主成分影响力度的重要指标[23],特征根越小,其方差贡献率越低,对数据的整体特征影响可忽略。表 2中是PCA分析后的前20个维度的特征根方差贡献率。PCA 1, PCA 2, PCA 3, …, PCA 14的特征根都大于1,其累计方差贡献率为99.604%,即前14个主成分反映了38个样本99.604%的特征信息,说明PCA分析后的数据可作为特征变量建立分类模型。剩余主成分数据略。
Table 2. Total variance explanation of PCA
component initial eigenvalues extraction sums of squared loadings total variance/% cumulative/% total variance/% cumulative/% PCA 1 443.569 51.758 51.758 443.569 51.758 51.758 PCA 2 262.099 30.583 82.342 262.099 30.583 82.342 PCA 3 59.006 6.885 89.227 59.006 6.885 89.227 PCA 4 34.696 4.049 93.275 34.696 4.049 93.275 PCA 5 13.935 1.626 94.901 13.935 1.626 94.901 PCA 6 10.131 1.182 96.084 10.131 1.182 96.084 PCA 7 8.449 0.986 97.069 8.449 0.986 97.069 PCA 8 7.474 0.872 97.942 7.474 0.872 97.942 PCA 9 3.945 0.460 98.402 3.945 0.460 98.402 PCA 10 3.294 0.384 98.786 3.294 0.384 98.786 PCA 11 3.001 0.350 99.136 3.001 0.350 99.136 PCA 12 1.507 0.176 99.312 1.507 0.176 99.312 PCA 13 1.360 0.159 99.471 1.360 0.159 99.471 PCA 14 1.138 0.133 99.604 1.138 0.133 99.604 PCA 15 0.773 0.09 99.694 PCA 16 0.620 0.072 99.766 PCA 17 0.447 0.052 99.818 PCA 18 0.339 0.040 99.858 PCA 19 0.269 0.031 99.889 PCA 20 0.211 0.025 99.914 -
特征根大于1且累计方差大于85%的主成分可提取并建立分类模型,但并不是绝对的,要根据具体情况进行综合判断。为了检验分类模型的准确度,通过RBF进行验证分析。为保证RBF验证分析的准确性,输入层将主成分分析后前37个主成分PCA 1,PCA 2,PCA 3,……,PCA 37作为变量因子,采用递增方法对隐层的神经元个数进行确定,从零开始,对神经元个数的逐个增加实现最大限度的降低误差,如果不满足网络设计精度则重复上述操作[24],直到满足精度。选择随机生成种子数为229176228,防止过度拟合集合为30.0%,当满足精度或者达到最大神经元个数时,模型终止,构建RBF水性木器漆分类的标准模型。
$准确率 = \frac{正确分类的样本个数}{总样本数} \times 100\% $%;$召回率 = \frac{正确分类的样本个数}{应该被分为此类的样本数} \times 100\% $。正确率与召回率两者之间存在相互制约的关系,一般地,正确率的上浮会导致召回率下沉;召回率上浮同时引起准确率下降,可以认为两者都相对较高情况作为理想分类。表 3中的数据是3维~37维的准确率与召回率,在15维下总体正确率最高,为78.9%。同时发现, 该维度下准确率与召回率符合理想状况,即可以将15维作为数据分类模型的最优维。
Table 3. Precision and recall in different dimensions
dimension precision/% recall/% overall
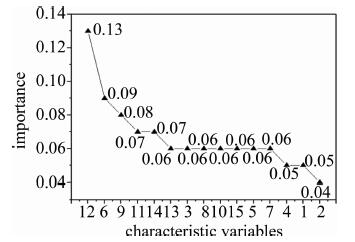
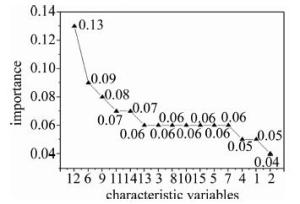
accuracy/%1 2 3 1 2 3 3 91.7 84.2 28.6 73.3 76.2 1.0 76.3 4 58.3 84.2 0.0 50.0 66.7 0.0 60.5 5 58.3 78.9 0.0 46.7 65.2 0.0 57.9 6 58.3 84.2 0.0 50.0 66.7 0.0 60.5 7 50.0 84.2 0.0 50.0 61.5 0.0 57.9 8 50.0 84.2 0.0 50.0 61.5 0.0 57.9 9 50.0 84.2 0.0 46.2 64.0 0.0 57.9 10 50.0 84.2 0.0 46.2 64.0 0.0 57.9 11 91.7 52.6 42.9 68.8 71.4 37.5 63.2 12 75.0 78.9 42.9 64.3 78.9 60.0 71.1 13 91.7 78.9 42.9 73.3 83.3 60.0 76.3 14 75.0 78.9 71.4 75.0 83.3 62.5 76.3 15 75.0 78.9 85.7 75.0 88.2 66.7 78.9 16 50.0 84.2 0.0 50.0 61.5 0.0 57.9 17 50.0 84.2 0.0 50.0 61.5 0.0 57.9 18 91.7 73.7 28.6 61.1 77.8 1.0 71.1 19 50.0 84.2 0.0 50.0 61.5 0.0 57.9 20 50.0 84.2 0.0 50.0 61.5 0.0 57.9 21 50.0 84.2 0.0 50.0 61.5 0.0 57.9 22 50.0 84.2 0.0 50.0 61.5 0.0 57.9 23 50.0 84.2 0.0 50.0 61.5 0.0 57.9 24 50.0 84.2 0.0 50.0 61.5 0.0 57.9 25 50.0 84.2 0.0 50.0 61.5 0.0 57.9 26 50.0 84.2 0.0 50.0 61.5 0.0 57.9 27 83.3 68.4 0.0 50.0 72.2 0.0 60.5 28 83.3 68.4 0.0 50.0 72.2 0.0 60.5 29 83.3 68.4 0.0 50.0 72.2 0.0 60.5 30 83.3 73.7 0.0 50.0 77.8 0.0 63.2 31 83.3 73.7 0.0 52.6 73.7 0.0 63.2 32 83.3 73.7 0.0 50.0 77.8 0.0 63.2 33 83.3 73.7 0.0 50.0 77.8 0.0 63.2 34 83.3 73.7 0.0 50.0 77.8 0.0 63.2 35 83.3 73.7 0.0 50.0 77.8 0.0 63.2 36 83.3 73.7 0.0 50.0 77.8 0.0 63.2 37 83.3 73.7 0.0 50.0 77.8 0.0 63.2 选取最优维度下这15个主成分作为特征变量进行分析。为了清楚地看出哪些特征变量的重要性相对更高,对这些变量的特征重要性展开分析。特征变量重要性是依据决策树中节点的增益来判断的,某个特征作为节点的次数越多,重要性越高[25]。分析得到该维度下的特征变量重要性(见图 1)。
从图 1中容易看出15个特征变量在做分类预测时的重要程度。特征12为区分贡献最大的特征,其重要性达0.13;其次为特征6,重要性为0.09;特征9的重要性为0.08;特征11和特征14重要性相同,都是0.07;特征13、特征3、特征8、特征10、特征15、特征5和特征7的重要性相同,都为0.06;特征4和特征1的重要性同为0.05;特征2的重要性最小,重要性为0.04,对模型区分的贡献最低。
选取特征变量重要性较高的特征12、特征6和特征9做RBF分析,发现正确率也是78.9%,所以只需要对这3个变量构建分类模型,可提升模型的计算速度。为了验证最优变量分类结果的优越性,将基于这3个变量分类结果的准确率与召回率与全波段的进行比较(见表 4)。
Table 4. Classification results of all-band data and optimal variable data
all band optimal variable precision/% recall/% precision/% recall/% CY 75.0 42.9 75.0 75.0 HC 68.4 76.5 78.9 88.2 QS 85.7 0.0 85.7 66.7 从表 4中看出,CY在全波段的准确率为75%,召回率为42.9%,最优变量的准确率不变,召回率相比比全波段高32.1个百分点; HC在全波段的准确率为68.4%,召回率为76.5,最优变量的准确率为78.9%,召回率为88.2%;QS在全波段的准确率为85.7%,召回率为0,最优变量准确率为85.7%,召回率为66.7%,分析认为,最优变量数据的分类模型结果理想,比全波段更有说服力。
通过RBF分析,得到37维下的准确率与召回率,选取最优维度(总体正确率最高)下具有代表性的3个特征变量构建RBF分类模型,再把分类结果与全波段数据的分类结果进行对比,发现最优变量的分类效果更好,科学有效地提高了模型的计算速度和准确率,实现了对37个木器漆样品快速有效分类。
-
本实验中利用傅里叶变换喇曼光谱结合主成分分析和径向基函数神经网络,对水性木器漆进行识别与分类,在快速检验、不损坏检材的前提下,构建RBF分类模型并对获得的数据进行分类鉴别,实现了对水性木器漆的有效分类。同时发现,降维后的总正确率为78.9%,导致正确率较低的原因可能是实验样本量的不足,训练样本集在建立分类模型的过程中不能精准地将相同品牌的特征总结。虽然本实验的样品量有限,但还是为法庭科学领域中水性木器漆的分类研究打开了新的方向。水性木器漆是犯罪现场中常见的物证之一,后期将针对水性木器漆的分类开展进一步研究,从实验方法和数据处理等多个角度寻找突破口,最终实现对水性木器漆的精准分类。
基于径向基函数的水性木器漆喇曼光谱鉴别
Raman spectrum identification of waterborne wood coating based on radial basis function
-
摘要: 水性木器漆是一种犯罪现场常见的微量物证,在法庭科学领域广受关注。为了实现对水性木器漆中复杂化学成分的检测分类,采用具有较高分辨能力和无损检验特点的喇曼光谱,结合主成分分析和径向基函数神经网络两种数据挖掘技术,对3种品牌共38个水性木器漆样本的喇曼光谱进行了数据分析。结果表明,径向基函数模型下可得到准确率为78.9%的分类识别。采用傅里叶变换喇曼光谱结合径向基函数模型实现对水性木器漆的鉴别与分类,为实践中木器漆的分类研究提供新思路。Abstract: Waterborne wood coating is a kind of trace evidence commonly found in crime scenes, and it is widely concerned in the forensic science field. In order to detect and classify the complex chemical components in waterborne wood paints, Raman spectrum, which has high resolving power and non-destructive testing characteristics, were used in this study. Combined with two data mining techniques of principal component analysis and radial basis function neural network, the Raman spectra of 38 waterborne wood lacquer samples from 3 brands were analyzed. The results show that the classification accuracy of 78.9% is obtained under the radial basis function model. Fourier Raman spectroscopy combined with radial basis function model was used to identify and classify waterborne wood coating, which provided new ideas for the classification of wood lacquers in practice.
-
Table 1. The details of 6 samples
number brand category manufacturer CY003 CHENYANG water-borne multifunctional paint CHENYANG CY005 CHENYANG water-borne multifunctional paint CHENYANG HC003 HUACAI water-based environmental protection paint CHAOMEIYAQI HC006 HUACAI water-based environmental protection paint CHAOMEIYAQI QS002 QUESHANG water-based anti-rust finish CHANGFENGHUANBAO QS009 QUESHANG waterborne furniture finish CHANGFENGHUANBAO Table 2. Total variance explanation of PCA
component initial eigenvalues extraction sums of squared loadings total variance/% cumulative/% total variance/% cumulative/% PCA 1 443.569 51.758 51.758 443.569 51.758 51.758 PCA 2 262.099 30.583 82.342 262.099 30.583 82.342 PCA 3 59.006 6.885 89.227 59.006 6.885 89.227 PCA 4 34.696 4.049 93.275 34.696 4.049 93.275 PCA 5 13.935 1.626 94.901 13.935 1.626 94.901 PCA 6 10.131 1.182 96.084 10.131 1.182 96.084 PCA 7 8.449 0.986 97.069 8.449 0.986 97.069 PCA 8 7.474 0.872 97.942 7.474 0.872 97.942 PCA 9 3.945 0.460 98.402 3.945 0.460 98.402 PCA 10 3.294 0.384 98.786 3.294 0.384 98.786 PCA 11 3.001 0.350 99.136 3.001 0.350 99.136 PCA 12 1.507 0.176 99.312 1.507 0.176 99.312 PCA 13 1.360 0.159 99.471 1.360 0.159 99.471 PCA 14 1.138 0.133 99.604 1.138 0.133 99.604 PCA 15 0.773 0.09 99.694 PCA 16 0.620 0.072 99.766 PCA 17 0.447 0.052 99.818 PCA 18 0.339 0.040 99.858 PCA 19 0.269 0.031 99.889 PCA 20 0.211 0.025 99.914 Table 3. Precision and recall in different dimensions
dimension precision/% recall/% overall
accuracy/%1 2 3 1 2 3 3 91.7 84.2 28.6 73.3 76.2 1.0 76.3 4 58.3 84.2 0.0 50.0 66.7 0.0 60.5 5 58.3 78.9 0.0 46.7 65.2 0.0 57.9 6 58.3 84.2 0.0 50.0 66.7 0.0 60.5 7 50.0 84.2 0.0 50.0 61.5 0.0 57.9 8 50.0 84.2 0.0 50.0 61.5 0.0 57.9 9 50.0 84.2 0.0 46.2 64.0 0.0 57.9 10 50.0 84.2 0.0 46.2 64.0 0.0 57.9 11 91.7 52.6 42.9 68.8 71.4 37.5 63.2 12 75.0 78.9 42.9 64.3 78.9 60.0 71.1 13 91.7 78.9 42.9 73.3 83.3 60.0 76.3 14 75.0 78.9 71.4 75.0 83.3 62.5 76.3 15 75.0 78.9 85.7 75.0 88.2 66.7 78.9 16 50.0 84.2 0.0 50.0 61.5 0.0 57.9 17 50.0 84.2 0.0 50.0 61.5 0.0 57.9 18 91.7 73.7 28.6 61.1 77.8 1.0 71.1 19 50.0 84.2 0.0 50.0 61.5 0.0 57.9 20 50.0 84.2 0.0 50.0 61.5 0.0 57.9 21 50.0 84.2 0.0 50.0 61.5 0.0 57.9 22 50.0 84.2 0.0 50.0 61.5 0.0 57.9 23 50.0 84.2 0.0 50.0 61.5 0.0 57.9 24 50.0 84.2 0.0 50.0 61.5 0.0 57.9 25 50.0 84.2 0.0 50.0 61.5 0.0 57.9 26 50.0 84.2 0.0 50.0 61.5 0.0 57.9 27 83.3 68.4 0.0 50.0 72.2 0.0 60.5 28 83.3 68.4 0.0 50.0 72.2 0.0 60.5 29 83.3 68.4 0.0 50.0 72.2 0.0 60.5 30 83.3 73.7 0.0 50.0 77.8 0.0 63.2 31 83.3 73.7 0.0 52.6 73.7 0.0 63.2 32 83.3 73.7 0.0 50.0 77.8 0.0 63.2 33 83.3 73.7 0.0 50.0 77.8 0.0 63.2 34 83.3 73.7 0.0 50.0 77.8 0.0 63.2 35 83.3 73.7 0.0 50.0 77.8 0.0 63.2 36 83.3 73.7 0.0 50.0 77.8 0.0 63.2 37 83.3 73.7 0.0 50.0 77.8 0.0 63.2 Table 4. Classification results of all-band data and optimal variable data
all band optimal variable precision/% recall/% precision/% recall/% CY 75.0 42.9 75.0 75.0 HC 68.4 76.5 78.9 88.2 QS 85.7 0.0 85.7 66.7 -
[1] TANG T, ZHOU G, LU Z G, et al. Effects of dehumidification drying environment on drying speed of one component waterborne wood top coating[J]. Applied Surface Science, 2016, 365(3): 131-135. [2] TANG T, BAI S H, ZHOU G, et al. Effect of dehumidification drying environment on surface gloss of one component waterborne wood top coating[J]. Applied Thermal Engineering, 2016, 102(1): 716-719. [3] UGULINO B, HERNANDEZ R E. Assessment of surface properties and solvent-borne coating performance of red oak wood produced by peripheral planning [J]. European Journal of Wood and Wood Products, 2017, 75(4):581-593. doi: 10.1007/s00107-016-1090-6 [4] GHOLAMIYAN H, TARMIAN A, RANJBAR Z, et al. Silane nanofilm formation by sol-gel processes for promoting adhesion of waterborne and solvent-borne coatings to wood surface[J]. Holzforschung, 2016, 70(5):429-437. doi: 10.1515/hf-2015-0072 [5] ALTGEN M, MILITZ H. Thermally modified Scots pine and Norway spruce wood as substrate for coating systems[J]. Journal of Coatings Technology and Research, 2017, 14(3):531-541. doi: 10.1007/s11998-016-9871-8 [6] MEIJER M, THURICH K, MILITZ H. Comparative study on penetration characteristics of modern wood coatings[J]. Wood Science and Technology, 1998, 32(5): 347-365. doi: 10.1007/BF00702791 [7] MARTINS E M, BORBA P F D S, SANTOS N E D, et al. The relationship between solvent use and BTEX concentrations in occupational environments[J]. Environmental Monitoring and Assessment, 2016, 188(11): 712-720. [8] LI J F, HUANG Y F, DING Y, et al. Shell-isolated nanoparticle-enhanced Raman spectroscopy[J]. Nature, 2010, 464(7287):392-395. doi: 10.1038/nature08907 [9] BUTLER H J, ASHTON L, BIRD B, et al. Using Raman spectroscopy to characterize biological materials[J]. Nature Protocols, 2016, 11(4): 664-687. doi: 10.1038/nprot.2016.036 [10] JERMYN M, MOK K, MERCIER J, et al. Intraoperative brain cancer detection with Raman spectroscopy in humans[J]. Science Translational Medicine, 2015, 7(274): 274ra19. [11] WANG W, XI X X, WANG B, et al. Raman spectrum analysis of forsythia leaves[J]. Laser Technology, 2011, 35(5):672-674(in Chinese). [12] FANG G, YIN L, LIU F, et al. Application research of fluorescence suppression based on differential Raman technique[J]. Laser Technology, 2019, 43(3):359-362(in Chinese). [13] PENIDO F D O, AUGUSTO C, PACHECO T, et al. Raman spectroscopy in forensic analysis: Identification of cocaine and other illegal drugs of abuse[J]. Journal of Raman Spectroscopy, 2016, 47(1): 28-38. doi: 10.1002/jrs.4864 [14] STEPHAN H, LAVEN M, ABDELOUAHID M, et al. Label-free raman spectroscopic imaging monitors the integral physiologically relevant drug responses in cancer cells[J]. Analytical Chemistry, 2015, 87(14): 7297-7304. doi: 10.1021/acs.analchem.5b01431 [15] SHEN B J, JIN L H, LIU Y X, et al. Study of intermolecular interactions between pterostilbene and human serum albumin by fluorescence spectrometry-surface enhanced raman spectroscopy[J]. Chinese Journal of Analytical Chemistry, 2017, 45(11):1613-1620(in Chinese). [16] KLINE N D, TRIPATHI A, MIRSAFAVI R, et al. Optimization of surface-enhanced raman spectroscopy conditions for implementation into a microfluidic device for drug detection[J]. Analytical Chemistry, 2016, 88(21):10513-10522. doi: 10.1021/acs.analchem.6b02573 [17] HU Y, FENG S, GAO F, et al. Detection of melamine in milk using molecularly imprinted polymers-surface enhanced Raman spectroscopy[J]. Food Chemistry, 2015, 176(6): 123-129. [18] LENZ R, ENDERS K, STEDMON C A, et al. A critical assessment of visual identification of marine microplastic using Raman spectroscopy for analysis improvement[J]. Marine Pollution Bulletin, 2015, 100(1): 82-91. doi: 10.1016/j.marpolbul.2015.09.026 [19] BUZZINI P, MASSONNET G. The analysis of colored acrylic, cotton, and wool textile fibers using micro-raman spectroscopy. Part 2: Comparison with the traditional methods of fiber examination[J]. Journal of Forensic Sciences, 2015, 60(3):712-720. doi: 10.1111/1556-4029.12654 [20] ZIEBA-PALUS J, BEATA M T. Application of infrared and raman spectroscopy in paint trace examination[J]. Journal of Forensic Sciences, 2013, 58(5):1359-1363. doi: 10.1111/1556-4029.12183 [21] WU Zh H, CUI X R, HUANG D Zh, et al. Spectral analysis of red blood cells in umbilical cord blood and children with congenital heart disease[J]. Laser Technology, 2012, 36(2):238-242(in Chinese). [22] AIT-SAHALIA Y, XIU D. Principal component analysis of high-frequency data[J]. Journal of the American Statistical Association, 2017, 144(525):1-17. [23] HE X L, WANG J F, WU F L, et al. Identification of the infrared spectra of tire rubber based on chemometrics[J]. Journal of Analytical Science, 2019, 35(3):357-361(in Chinese). [24] CHEN G Q, WEI B L, WANG J, et al. Quantitative determination of melamine by fluorescence spectroscopy and radial basis function neural networks[J]. Spectroscopy and Spectral Analysis, 2010, 30(1):239-242(in Chinese). [25] GONG Y Ch, DU Ch H, ZHANG Y N, et al. Prediction of blood glucose based on principal component and GBDT[J]. Mathematics in Practice and Theory, 2019, 49(14):116-122(in Chinese). -


 网站地图
网站地图

 下载:
下载: