-
双折射光纤环镜(birefringence fiber loop mirror,Bi-FLM)传感器不仅可以作为可调谐光滤波器[1],还广泛应用于应变[2-5]、振动[6-7]、扭矩[8-9]等各类传感器。外界传感量的变化改变Bi-FLM传感器的干涉光谱,Bi-FLM传感器通过监测干涉光谱的变化来感知外界传感量。Bi-FLM传感器通常通过监测干涉光谱波长的变化来反推外界传感量的大小[10-18],即通过波长解调实现传感。波长解调的优点是不受光源强度波动影响,但波长解调的最大缺点是不能实现在线测量。作者根据Bi-FLM干涉光谱任意4个相邻波谷波长相对位置蕴含着应变信息的特点,曾研究通过任意4个相邻波谷波长及双折射光纤初始条件计算应变大小。该方法无需人为判断,有助于促进传感器与计算机有效对接,实现在线测量, 但该方法需要4个相邻波谷的波长,包含3个周期的干涉波形,需要的信息量较多。双折射光纤长度越短,Bi-FLM干涉光谱周期越大[13],在一定的光源波长范围内,光纤长度较短的Bi-FLM可能没有足够的波谷点,导致无法计算。本文中提出通过一组相邻的波峰、波谷波长及双折射光纤初始条件计算应变大小,以此实现Bi-FLM应变传感器在线测量。该方法仅需0.5个周期的干涉波形,需要的信息量小,能够解决传感光纤长度较短的Bi-FLM传感器蕴含的信息量不足的问题。
-
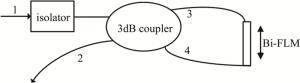
图 1为Bi-FLM传感器原理图。将一根传统的单模3dB耦合器的端口3和端口4熔接一段双折射光纤作为传感元件,即构成Bi-FLM传感器。输入光源经端口1、光隔离器进入3dB耦合器,按1:1分成从端口3顺时针和端口4逆时针相向传输的两束光,由于双折射光纤的双折射效应,最后两束光在端口2相遇并产生干涉。外界传感量的变化导致干涉光谱的变化,根据干涉光谱的变化,反推外界传感量的大小,以此实现传感。
Bi-FLM传感器初始干涉光谱表达式为[19]:
$ T(\lambda ) = \frac{{1 - {\rm{cos}}\left( {\frac{{2\pi {L_0}{B_0}}}{\lambda }} \right)}}{2} = \frac{{1 - {\rm{cos}}\theta }}{2} $
(1) 式中,λ为干涉光谱波长,T(λ)为干涉光谱强度,相角θ=2πL0B0/λ,L0为光纤初始长度,B0为光纤初始双折射率。
当双折射光纤受轴向应变后,相角变化量Δθ为[19]:
$ \Delta \theta = \frac{{2\pi {L_0}}}{\lambda }({B_0} + k){\varepsilon _z} $
(2) 式中,εz=ΔL/L0=(L′-L0)/L0为双折射光纤轴向应变,单位为ε,其中L′为双折射光纤受应变后的长度; k是双折射应变系数,单位为1/ε,即光纤受1ε后双折射率变化大小。
由(2)式可得通过L′表示的Δθ表达式为:
$ \Delta \theta = \frac{{2\pi }}{\lambda }({B_0} + k)({L^\prime } - {L_0}) $
(3) 由(1)式、(2)式可得通过εz表示的受轴向应变后的Bi-FLM干涉光谱表达式为:
$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T^\prime }(\lambda ) = \frac{{1 - {\rm{cos}}(\theta + \Delta \theta )}}{2} = \\ \frac{{1 - {\rm{cos}}\left[ {\frac{{2\pi {L_0}{B_0}}}{\lambda } + \frac{{2\pi {L_0}}}{\lambda }({B_0} + k){\varepsilon _z}} \right]}}{2} \end{array} $
(4) (4) 式是通过双折射光纤所受应变εz描述干涉光谱T′(λ),与参考文献[4]、参考文献[6]、参考文献[20]一致, 用于与下面推导的计算应变的理论表达式对比,以校验本文中推导的表达式正确性。
由(1)式、(3)式可得通过L'表示的受轴向应变后的干涉光谱表达式为:
$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T^\prime }(\lambda ) = \frac{{1 - {\rm{cos}}(\theta + \Delta \theta )}}{2} = \\ \frac{{1 - {\rm{cos}}\left[ {\frac{{2\pi {L_0}{B_0}}}{\lambda } + \frac{{2\pi {L_0}}}{\lambda }({B_0} + k)({L^\prime } - {L^\prime }_0)} \right]}}{2} \end{array} $
(5) 欲使(5)式对应干涉光谱T′(λ)的值最小,则:
$ \frac{{2\pi {L_0}{B_0}}}{{{\lambda _n}}} + \frac{{2\pi }}{{{\lambda _n}}}({B_0} + k)({L^\prime } - {L_0}) = 2n\pi $
(6) 式中,n为整数,λn为整数n对应的波谷波长,其它依此类推。
由(6)式解出:
$ {\lambda _n} = \frac{{{L_0}{B_0} + ({B_0} + k)({L^\prime } - {L_0})}}{n} $
(7) 欲使(5)式对应干涉光谱T′(λ)的值最大,则:
$ \frac{{2\pi {L_0}{B_0}}}{{{\lambda _n}^\prime }} + \frac{{2\pi }}{{{\lambda _n}^\prime }}({B_0} + k)({L^\prime } - {L_0}) = (2n + 1)\pi $
(8) 式中,λn′为整数n对应的波峰波长,其它依此类推。
由(8)式解出:
$ {\lambda _n}^\prime = \frac{{{L_0}{B_0} + ({B_0} + k)({L^\prime } - {L_0})}}{{n + 0.5}} $
(9) 由(7)式可得:
$ \frac{{n{\lambda _n} - {L_0}{B_0}}}{{({B_0} + k)}} + {L_0} = {L^\prime } $
(10) 由(9)式可得:
$ \frac{{(n + 0.5){\lambda _n}^\prime - {L_0}{B_0}}}{{{B_0} + k}} + {L_0} = {L^\prime } $
(11) 由(10)式=(11)式可得:
$ n = 0.5{\lambda _n}^\prime /({\lambda _n} - {\lambda _n}^\prime ) $
(12) 由(12)式代入(10)式可得:
$ {L^\prime } = \frac{{\frac{{0.5{\lambda _n}^\prime {\lambda _n}}}{{{\lambda _n} - {\lambda _n}^\prime }} + {L_0}k}}{{{B_0} + k}} $
(13) 由(13)式可知,双折射光纤受轴向应变后的绝对长度L′可以由任意一组相邻的波峰波长λn′、波谷波长λn、光纤初始长度L0、光纤初始双折射率B0和双折射应变系数k求出,再将L′代入εz=ΔL/L0=(L′-L0)/L0计算双折射光纤所受应变大小。该方法可以由任意一组相邻的波峰波长、波谷波长及光纤初始条件求出双折射光纤所受应变大小。由(13)式可知,该方法与选定的监测点无关,无需进行传感器的校准;该方法无需人为判断干涉光谱左移还是右移,无需人为判断是否是周而复始的干涉光谱,有助于实现在线测量;该方法只需包含0.5个周期的干涉波形,需要的信息量更少,可以实现双折射光纤长度更短的Bi-FLM传感器的在线测量。
根据(7)式、(9)式可得:
$ {{\lambda _n} = \frac{{{L_0}[{B_0} + ({B_0} + k){\varepsilon _z}]}}{n}} $
(14) $ {{\lambda _n}^\prime = \frac{{{L_0}[{B_0} + ({B_0} + k){\varepsilon _z}]}}{{n + 0.5}}} $
(15) 当(14)式、(15)式n值相同时,波谷与波峰相邻。由(14)式可知,当双折射光纤所受应变εz为正时,因为波长必须为正数,故n为正,此时λn>λn′;当双折射光纤所受应变εz为负应变且足够使n为负数时,此时λn′>λn。由(14)式可知,因为波长必须为正数,要使n为负数,则:
$ {B_0} + ({B_0} + k){\varepsilon _z} < 0 $
(16) 由(16)式可得:
$ {\varepsilon _z} < \frac{{ - {B_0}}}{{{B_0} + k}} $
(17) 假设双折射光纤长度L0=0.1m,双折射率B0=2.6×10-4,双折射应变系数k=7.3×0.001/ε,经计算需满足εz < -0.0343915343915344ε,即εz < -34391.5343915344με时,才能使n为负数,该应变是个极大的负应变,一般情况下难于产生如此大的负应变,故一般情况下n为正。
欲使(5)式对应干涉光谱T′(λ)的值最大,则可令:
$ \frac{{2\pi {L_0}{B_0}}}{{{\lambda _n}^\prime }} + \frac{{2\pi }}{{{\lambda _n}^\prime }}({B_0} + k)({L^\prime } - {L_0}) = (2n - 1)\pi $
(18) 由(18)式可得:
$ {\lambda _n}^\prime = \frac{{{L_0}{B_0} + ({B_0} + k)({L^\prime } - {L_0})}}{{n - 0.5}} $
(19) 由(19)式可得:
$ \frac{{(n - 0.5){\lambda _n}^\prime - {L_0}{B_0}}}{{{B_0} + k}} + {L_0} = {L^\prime } $
(20) 由(10)式=(20)式可得:
$ n = \frac{{0.5{\lambda _n}^\prime }}{{{\lambda _n}^\prime - {\lambda _n}}} $
(21) 由(21)代入(10)式可得:
$ {L^\prime } = \frac{{\frac{{0.5{\lambda _n}^\prime {\lambda _n}}}{{{\lambda _n}^\prime - {\lambda _n}}} + {L_0}k}}{{{B_0} + k}} $
(22) 根据(19)式可得:
$ {\lambda _n}^\prime = \frac{{{L_0}[{B_0} + ({B_0} + k){\varepsilon _z}]}}{{n - 0.5}} $
(23) 当(14)式、(23)式中的n值相同时,波谷与波峰相邻。当εz>0时,n为正,满足λn′>λn,应用(22)式计算双折射光纤受轴向应变后的绝对长度L′,并以此计算双折射光纤所受应变大小;εz$ \ll $0且足够使n为负数时,满足λn>λn′,应用(22)式计算L′,并以此计算应变大小。
比较(13)式、(22)式可知:一般情况下n为正,满足λn′ < λn时使用(13)式;满足λn′>λn时使用(22)式。若已知任意一组相邻的波峰波长、波谷波长,无需判断波峰波长λn′、波谷波长λn谁大谁小,(13)式、(22)式统一为(24)式:
$ {L^\prime } = \frac{{\frac{{0.5{\lambda _n}^\prime {\lambda _n}}}{{\left| {{\lambda _n}^\prime - {\lambda _n}} \right|}} + {L_0}k}}{{{B_0} + k}} $
(24) 但当应变εz $ \ll $0且足够使n为负数时,应区分波峰波长、波谷波长的大小,选择合适的公式计算双折射光纤受轴向应变的大小。εz$ \ll $0且足够使n为负数时,满足λn′>λn,应用(13)式; εz$ \ll $0且足够使n为负数时,满足λn>λn′,应用(22)式。由前述可知,一般情况下难于产生足够的大负应变使n为负数,故一般情况下n为正。下面就n为正时展开讨论。
-
为了验证(24)式的正确性,计算如下:假设双折射光纤长度L0=0.1m,双折射率B0=2.6×10-4,双折射应变系数k=7.3×0.001/ε,选取波长范围为典型通讯波长1550nm附近,横坐标λ步长增量设置为0.0001nm,εz=200με时由(4)式绘制的干涉光谱如图 2所示。当εz为确定值时,干涉光谱强度T′(λ)是随λ变化的余弦函数,无量纲。从图 2可以看出,当双折射光纤长度L0=0.1m时,波长在1460nm~1660nm范围内只包含2个相邻波谷波长λn和λn+1、2个相邻波峰波长λn′和λn+1′,不包含4个相邻波谷的波长信息,无法用4个波谷波长信息计算应变。按波长由小到大,分别以图中的λn+1′/λn+1,λn+1/λn′,λn′/λn两两组合为一组,组成3组波峰波长、波谷波长,其中λn+1′ < λn+1,λn′ < λn两组是波峰波长 < 波谷波长,满足(13)式,λn+1 < λn′一组是波峰波长>波谷波长,满足(22)式,但无需判断波峰波长、波谷波长谁大谁小,结合光纤初始长度L0、光纤初始双折射率B0和双折射应变系数k,应用(24)式编程求解双折射光纤受轴向应变后的绝对长度L′,再将L′代入εz=ΔL/L0=(L′-L0)/L0计算双折射光纤所受应变大小。计算应变及误差如表 1所示。表中, $\text { 误差 }=\frac{\text { 计算应变 }-\text { 给定应变 }}{\text { 给定应变 }} \times 100 \% $。
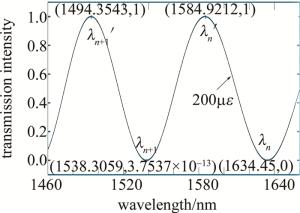
Figure 2. The Bi-FLM interference spectra by a set of adjacent wave-valley and wave-peak wavelengths near 1550nm
Table 1. Calculating strain results by a set of adjacent wave-valley and wave-peak wavelengths near 1550nm
given strain/με wave-peak wavelength/nm wave-valleywavelength/nm calculated strain/με error/% 100 1490.0343 1533.8588 100.0296 0.0296 1580.3394 1533.8588 99.9776 -0.0224 1580.3394 1629.725 100.0044 0.0044 200 1494.3543 1538.3059 199.9981 -0.0010 1584.9212 1538.3059 200.0222 0.0111 1584.9212 1634.45 199.9913 -0.0044 300 1498.6743 1542.7529 300.0431 0.0144 1589.503 1542.7529 299.9903 -0.0032 1589.503 1639.175 299.9782 -0.0073 400 1502.9943 1547.2 400.0116 0.0029 1594.0848 1547.2 400.0349 0.0087 1594.0848 1643.9 399.9651 -0.0087 500 1507.3143 1551.6471 499.9801 -0.0040 1598.6667 1551.6471 500.0075 0.00149 1598.6667 1648.625 500.0240 0.0048 600 1511.6343 1556.0941 600.0251 0.0042 1603.2485 1556.0941 599.9756 -0.0041 1603.2485 1653.35 600.0109 0.0018 700 1514.9543 1560.5412 699.9936 -0.0009 1607.8303 1560.5412 700.0202 0.0029 1607.8303 1658.075 699.9978 -0.0003 800 1520.2743 1564.9882 800.0386 0.0048 1612.4121 1564.9882 799.9883 -0.0015 1612.4121 1662.8 799.9847 -0.0019 900 1524.5943 1569.4353 900.0071 0.0008 1616.9939 1569.4353 900.0329 0.0037 1616.9939 1667.525 899.9716 -0.0034 从表 1可以看出,统一应用(24)式便可计算双折射光纤受轴向应变大小,计算应变与给定应变基本一致。存在一定误差是由于(4)式绘制的Bi-FLM干涉光谱波形横坐标λ步长增量设置为0.0001nm,而非连续步长,导致某些波峰的纵坐标不完全等于1,或某些波谷的纵坐标不完全等于0,只是近似意义上的波峰波谷,如图 2中波谷点(1538.3059,3.7537×10-13)纵坐标不完全等于0。因此, 计算的应变也是近似接近理论值,从而与给定应变存在一定误差。
-
从理论上推导出由1组相邻的波峰波长、波谷波长及其双折射光纤初始长度、初始双折射率和初始双折射应变系数计算双折射光纤所受应变后的绝对长度,从而计算应变的方法, 并进一步通过数值计算验证理论的正确性。
只要图形包含1组相邻的波峰波长λn′、波谷波长λn,一般情况下,无需区分波峰波长、波谷波长的大小,便可计算双折射光纤受轴向应变后的绝对长度,从而计算应变。但当应变εz$ \ll $0且足够大时,应区分波峰波长、波谷波长的大小,选择合适的公式计算双折射光纤受轴向应变的大小。由1组相邻的波峰波长、波谷波长及其双折射光纤初始条件计算应变的方法与选定的监测点无关,无需进行传感器的校准;无需人为判断干涉光谱左移还是右移,无需人为判断是否是周而复始的干涉光谱,有助于实现在线测量;只需包含0.5个周期的干涉波形,需要的信息量更少,可以实现双折射光纤长度更短的Bi-FLM传感器的在线测量。
一组波峰波谷实现光纤环镜传感器在线测量
On-line measurement of a fiber loop mirror sensor using a set of adjacent wave-valley and wave-peak wavelengths
-
摘要: 为了实现传感光纤长度较短的双折射光纤环镜(Bi-FLM)传感器的在线测量,提出通过一组相邻的波峰波谷波长实现Bi-FLM应变传感器在线测量的方法。采用典型通讯波长1550nm附近的波峰波长、波谷波长及其双折射光纤初始条件,计算了应变大小。结果表明,该方法计算应变均与给定应变基本吻合,3组不同的组合方式计算的应变与给定应变的最大误差为0.0296%,最小误差为-0.0003%;该方法无需人为判断,有助于实现计算机在线测量; 与监测点无关,无需校准; 只需0.5个周期的干涉波形,需要的信息量少。这一结果对实现传感光纤长度较短的Bi-FLM传感器在线测量是有帮助的。Abstract: In order to realize the on-line measurement of a birefringence fiber (BF) loop mirror (Bi-FLM) strain sensor with a short BF, the theoretical on-line measurements expression of a Bi-FLM strain sensor using a set of adjacent wave-valley and wave-peak wavelengths was deduced. The adjacent wave-valley and wave-peak wavelengths were near 1550nm and the BF initial conditions were used to calculate strain. The maximum error and minimum error of strain calculated by three different wavelengths combination were 0.0296% and -0.0003%, respectively. The result shows that the calculated strains are basically consistent with the given strains. The method doesn't need human judgment. So it is helpful to realize on-line measurement by computer. The method is unrelated to the monitoring point. So the Bi-FLM sensor isn't calibrated. In addition, the method requires less information and only needs 0.5 period of interference waveform. So it is helpful to realize the on-line measurement of a Bi-FLM sensor with a short BF.
-
Table 1. Calculating strain results by a set of adjacent wave-valley and wave-peak wavelengths near 1550nm
given strain/με wave-peak wavelength/nm wave-valleywavelength/nm calculated strain/με error/% 100 1490.0343 1533.8588 100.0296 0.0296 1580.3394 1533.8588 99.9776 -0.0224 1580.3394 1629.725 100.0044 0.0044 200 1494.3543 1538.3059 199.9981 -0.0010 1584.9212 1538.3059 200.0222 0.0111 1584.9212 1634.45 199.9913 -0.0044 300 1498.6743 1542.7529 300.0431 0.0144 1589.503 1542.7529 299.9903 -0.0032 1589.503 1639.175 299.9782 -0.0073 400 1502.9943 1547.2 400.0116 0.0029 1594.0848 1547.2 400.0349 0.0087 1594.0848 1643.9 399.9651 -0.0087 500 1507.3143 1551.6471 499.9801 -0.0040 1598.6667 1551.6471 500.0075 0.00149 1598.6667 1648.625 500.0240 0.0048 600 1511.6343 1556.0941 600.0251 0.0042 1603.2485 1556.0941 599.9756 -0.0041 1603.2485 1653.35 600.0109 0.0018 700 1514.9543 1560.5412 699.9936 -0.0009 1607.8303 1560.5412 700.0202 0.0029 1607.8303 1658.075 699.9978 -0.0003 800 1520.2743 1564.9882 800.0386 0.0048 1612.4121 1564.9882 799.9883 -0.0015 1612.4121 1662.8 799.9847 -0.0019 900 1524.5943 1569.4353 900.0071 0.0008 1616.9939 1569.4353 900.0329 0.0037 1616.9939 1667.525 899.9716 -0.0034 -
[1] JI Zh J, WU X N, YIN Y, et al. Tunable optical filters based on high birefringence fiber loop mirrors[J]. Laser Technology, 2014, 38(1):54-57(in Chinese). [2] ZHAO C L, ZHAO J, JIN W, et al. Simultaneous strain and temperature measurement using a highly birefringence fiber loop mirror and a long-period grating written in a photonic crystal fiber[J]. Optics Communications, 2009, 282(20):4077-4080. doi: 10.1016/j.optcom.2009.07.002 [3] GONG H, CHAN C C, CHEN L, et al.Strain sensor realized by using low-birefringence photonic-crystal-fiber-based Sagnac loop[J]. IEEE Photonics Technology Letters, 2010, 22(16):1238-1240. doi: 10.1109/LPT.2010.2053025 [4] JIANG Y, ZENG J, LIANG D K, et al. The influences of polarization-maintaining fiber length and sensing length on axial strain sensitivity of polarization-maintaining fiber loop mirror[J]. Journal of Intelligent Material Systems and Structures, 2014, 25(15):1959-1964. doi: 10.1177/1045389X13512905 [5] FRAZAO O, BAPTISTA J M, SANTOS J L. Temperature-independent strain sensor based on a Hi-Bi photonic crystal fiber loop mirror[J]. IEEE Sensors Journal, 2007, 7(10):1453-1455. [6] JIANG Y, LIANG D K, LU J Y. Voltage demodulation and vibration monitoring based on a polarization maintaining fiber loop mirror[J]. Journal of Intelligent Material Systems and Structures, 2017, 28(13):1832-1838. doi: 10.1177/1045389X16679283 [7] LEANDRO D, LOPEZ-AMO M. All-PM fiber loop mirror interferometer analysis and simultaneous measurement of temperature and mechanical vibration[J]. Journal of Lightwave Technology, 2018, 36(4):1105-1111. doi: 10.1109/JLT.2017.2761121 [8] ZU P, CHAN C C, JIN Y X, et al. A temperature-insensitive twist sensor by using low-birefringence photonic-crystal-fiber-based sagnac interferometer[J]. IEEE Photonics Technology Letters, 2011, 23(13): 920-922. doi: 10.1109/LPT.2011.2143400 [9] SILVA R M, FERREIRA M S, FRAZO O. Temperature independent torsion sensor using a high-birefringent Sagnac loop interferometer[J]. Optics Communications, 2012, 285(6): 1167-1170. doi: 10.1016/j.optcom.2011.11.119 [10] NOH T K, RYU U C, LEE Y W. Compact and wide range polarimetric strain sensor based on polarization-maintaining photonic crystal fiber[J]. Sensors and Actuators: Physical, 2014, A213(7): 89-93. [11] WU C, TSE M L V, LIU Z, et al. In-line microfluidic refractometer based on C-shaped fiber assisted photonic crystal fiber Sagnac interferometer[J]. Optics Letters, 2013, 38(17): 3283-3286. doi: 10.1364/OL.38.003283 [12] GONG H P, SONG H F, ZHANG S L. Curvature sensor based on hollow-core photonic crystal fiber Sagnac interferometer[J]. IEEE Sensors Journal, 2014, 14(3): 777-779. doi: 10.1109/JSEN.2013.2283580 [13] JIANG Y, ZHANG C Z, LIANG D K, et al. Optimal research on the strain sensitivity of polarization maintaining fiber loop mirror[J]. Spectroscopy and Spectral Analysis, 2017, 37(5): 1576-1580(in Chinese). [14] ZHANG Y N, PENG H, ZHOU T, et al. Hydrogen sensor based on high-birefringence fiber loop mirror with sol-gel Pd/WO3 coating[J]. Sensors and Actuators: Chemical, 2017, B248:71-76. [15] WANG J, LIANG H, DONG X, et al. A temperature-insensitive relative humidity sensor by using polarization maintaining fiber-based Sagnac Interferometer[J]. Microwave & Optical Technology Letters, 2013, 55(10):2305-2307. [16] ZHAO Ch L, WANG Zh, ZHANG Sh, et al. Phenomenon in an alcohol not full-filled temperature sensor based on an optical fiber Sag-nac interferometer[J]. Optics Letters, 2012, 37(22):4789. doi: 10.1364/OL.37.004789 [17] ZHANG J, QIAO X, GUO T, et al. Highly-sensitive temperature sensor using a Hi-Bi fiber tip probe[J]. IEEE Sensors Journal, 2012, 12(6):2077-2080. doi: 10.1109/JSEN.2012.2183866 [18] JIANG Y, LIANG D K, ZENG J, et al. Research on axial strain sensitivity of high-birefringence fiber loop mirrorr[J]. Spectroscopy and Spectral Analysis, 2012, 32(12): 3367-3371(in Chinese). [19] QIAN W W, ZHAO C L, DONG X Y. Intensity measurement based temperature-independent strain sensor using a highly birefringent photonic crystal fiber loop mirror[J]. Optics Communications, 2010, 283(24): 5250-5254. doi: 10.1016/j.optcom.2010.07.062 [20] JIANG Y, YU M J. Influence of birefringence fibre length on demodulation sensitivity based on a fibre loop mirror sensor[J]. IET Optoelectronics, 2018, 12(5): 254-257. -


 网站地图
网站地图

 下载:
下载:


