-
近年来,在应用市场多元激励的作用下,无人机(unmarned aerial vehide,UAV)的研发经历了前所未有的变革。伴随着各种单一功能和多用途军用无人机实践应用的日益成熟化和产品化,无人机在民事领域的应用前景也越来越广阔。与此同时,用无人机执行任务与反无人机介入的斗争也愈演愈烈。在应用市场、任务背景和应对多重挑战等因素的作用下,无人机的独立性、自主性、实时性要求越来越高。因此,如何快速准确地获取无人机和目标的飞姿信息,并将之高效精准地转化为无人机的飞控参量成为无人机迈向智能化的关键环节[1]。
在无人机领域的研究中,基于视觉图像的位姿信息解算与参量转换研究正逐渐成为无人机自主化研究的热点,其核心是从连续的2维视觉图像及高度信息中获取无人机六自由度信息,利用牛顿力学和动量力矩等定理完成运动方程的构建和位姿信息的转换。参考文献[2]中通过对比无人机输入航迹与自身航迹的偏差,计算方向向量与加速度向量,利用比例-积分-微分(proportion-integration-differentiation, PID)控制算法完成无人机航迹和姿态进行控制。参考文献[3]中提出了一种结合学习特征的图像视觉伺服方法,利用统一投影模型, 分析了虚拟单位球体投影的解耦视觉伺服方法,研究了结合非线性模型预测控制的球体投影约束视觉伺服控制方法,并设计出结合离散化参考轨迹的无标定视觉预测控制算法。参考文献[4]中介绍了神经网络补偿结构的作用和设计方法, 基于无人机非线性姿态运动学和动力学模型设计了基于神经网络补偿的动态逆控制器,并进行了数学仿真实验。本文中主要进行无人机飞行六自由度信息的解算、运动模型转换以及动态跟踪方法的研究,并通过仿真实验对所提出的方法进行验证。
-
经过应用环境的选择和淘汰,无人机主要分固定翼、旋翼和直升机三大类,其中基于视觉导航跟踪及自主控制的研究又以旋翼无人机为主。旋翼无人机包括四旋翼、六旋翼和其它多旋翼无人机,四旋翼无人机又分为“十”型和“X”型两类[5]。作者以“十”型无人机为例, 进行了相关理论研究和仿真实验。
-
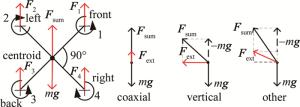
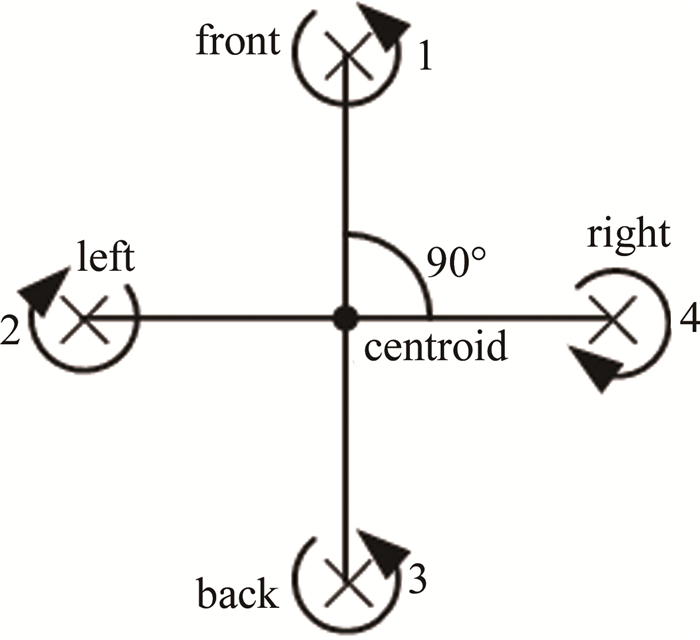
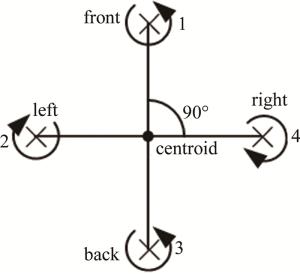
“十”型四旋翼无人机的结构如图 1所示。从图中可以看出两条机臂成90°相交于无人机的质心,1号~4号旋翼和电机分别安装于无人机飞行空间的前后左右4个方位,其结构、大小完全一样,且关于质心对称,每个旋翼和电机距离质心的长度相同,电机控制旋翼转速产生升力。在调整无人机飞行姿态时,通过电机调整旋翼的转速,改变旋翼的总力矩。转速调整越大,总力矩变化越大,无人机飞姿调整就越快。由牛顿定理可知,旋翼在旋转的同时,会向电机施加一个反作用力(又称反扭矩),为了消除这种反作用力,就需要在同一方向上施加另一种反方向的力[6]。因此,四旋翼无人机的4个旋翼中相邻两个旋翼的方向是相反的。在无人机飞行时,1号、3号旋翼和2号、4号旋翼产生的顺时针和逆时针反作用力相互抵消,无人机就可以保持平稳飞行。
-
展开无人机控制原理的分析之前,先介绍无人机飞行的六自由度信息,分为质心的3个沿轴移动自由度和3个绕轴转动自由度,分别对应无人机的空间位置(前后量x,侧向量y,升降量z)和无人机姿态(俯仰角θ,滚转角ϕ,偏航角ψ),即六自由度信息{x, y, z, θ, ϕ, ψ},或六自由度速度信息{$\dot x, \dot y, \dot z, \dot \theta , \dot \phi , \dot \psi $},或六自由度加速度信息{$\ddot{x}, \ddot{y}, \ddot{z}, \ddot{\theta}, \ddot{\phi}, \ddot{\psi}$} [7-8]。
无人机的飞行模式对应其六自由度信息,即前后、侧向、升降、俯仰、滚转和偏航运动。四旋翼无人机的不同飞行模式主要通过调整4个控制参量,使4个旋翼电机产生不同的旋转速度,提供4个不同大小的升力(累计为总升力Fsum)与重力mg(m为质量,g为重力加速度)矢量合成,产生指定方向和角度的外力Fext,控制无人机按照外力的方向飞行,如图 2所示。当外力方向与重力方向同轴时,无人机进行悬停、升降飞行,当外力方向与重力方向垂直时,无人机进行横移、偏航飞行,当外力方向与重力方向成其它角度时,无人机进行俯仰、滚转飞行。
-
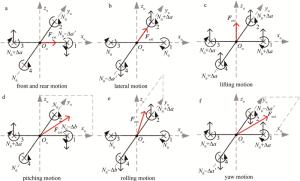
四旋翼无人机可进行6个自由度的飞行运动,但是只有4个独立的控制输入量,因此其是1种欠驱动系统。由牛顿定理可知, 升力随着转速的变化而变化,所以通过调节旋翼电机的转速就可以控制无人机的飞行姿态。无人机处于悬停状态时,4个旋翼提供的合力刚好等于无人机自身的重力,即外力Fext=0,设定此时旋翼的转速为N0,当改变部分或全部旋翼的转速时,外力Fext≠0,无人机就会按照外力的方向进行飞行,如图 3所示。图中Δa, Δb, Δa′为旋翼的转速调整变量,其中Δa, Δa′为一组对应的变量,当同一轴上的旋翼分别为N0+Δa, N0-Δa时,无人机只存在此轴上的外力,此时无人机沿该轴做直线运动,如图 3a~图 3c所示;当同一轴上的旋翼分别为N0+Δa, N0-Δb时,无人机存在该轴与z轴组成平面的外力,此时无人机绕另一轴做绕轴运动,如图 3d~图 3e所示;当不同轴上的旋翼分别为N0+Δa, N0-Δa时,无人机存在Ouxuyu平面的外力,此时无人机绕z运动,如图 3f所示。
-
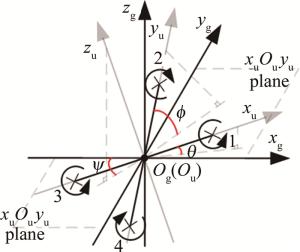
无人机飞行过程中有两个通用的坐标系,即无人机质心坐标u系Ouxuyuzu和地面坐标g系Ogxgygzg[9-10]。与不断变化的质心坐标系不同,地面坐标系是固定的,如图 4所示。为便于理解,必须先将无人机的姿态角进行明确的定义,从图中可以看出,俯仰角θ是质心坐标系xu轴与地面坐标系Ogxgyg平面的夹角,以Ogxgyg平面上方为正;滚转角ϕ是质心坐标系yu轴与地面坐标系Ogxgyg平面的夹角,以Ogxgyg平面上方为正;偏航角ψ是质心坐标系zu轴在地面坐标系Ogxgyg平面的投影与地面坐标系xg轴夹角,角度值以xg轴为起点,以东偏北逆时针方向为正。
-
四旋翼无人机运动方程主要包括物像关系式、质心运动方程和地面坐标运动方程[11-12],如下所示:
$ \left[ {\begin{array}{*{20}{c}} j\\ i\\ 1 \end{array}} \right] = {\mathit{\boldsymbol{C}}_0}\left[ {\begin{array}{*{20}{c}} {{x_{\rm{u}}}}\\ {{y_{\rm{u}}}}\\ 1 \end{array}} \right],{\mathit{\boldsymbol{C}}_0} = \left[ {\begin{array}{*{20}{c}} {f/{\rm{d}}x}&0&{{j_{\mathit{0}}}}\\ 0&{f/{\rm{d}}y}&{{i_{\mathit{0}}}}\\ 0&0&1 \end{array}} \right] $
(1) $ \left[ {\begin{array}{*{20}{c}} {{x_{\rm{g}}}}\\ {{y_{\rm{g}}}}\\ {{z_{\rm{g}}}} \end{array}} \right] = {\mathit{\boldsymbol{L}}_{{\rm{u,g}}}}\left[ {\begin{array}{*{20}{c}} {{x_{\rm{u}}}}\\ {{y_{\rm{u}}}}\\ {{z_{\rm{u}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{x_{{\rm{u,0}}}}}\\ {{y_{{\rm{u,0}}}}}\\ {{z_{{\rm{u,0}}}}} \end{array}} \right] $
(2) $ m\left[ {\begin{array}{*{20}{c}} {{{\ddot x}_{\rm{g}}}}\\ {{{\ddot y}_{\rm{g}}}}\\ {{{\ddot z}_{\rm{g}}}} \end{array}} \right] = mg\left[ {\begin{array}{*{20}{l}} 0\\ 0\\ 1 \end{array}} \right] - {\mathit{\boldsymbol{L}}_{{\rm{u,g}}}}{\mathit{\boldsymbol{F}}_{{\rm{sum}}}}\left[ {\begin{array}{*{20}{l}} 0\\ 0\\ 1 \end{array}} \right] - \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{c}} {{{\dot x}_{\rm{g}}}}\\ {{{\dot y}_{\rm{g}}}}\\ {{{\dot z}_{\rm{g}}}} \end{array}} \right] $
(3) (1) 式为物像关系式,式中, C0为相机已知的内参系数,其中dx, dy为像元素大小,(iO, jO)为质心Ou在像平面的坐标,f为相机的焦距;(2)式为无人机质心运动方程,式中, (xu, 0, yu, o, zu, o)为无人机在g系的初始坐标,(xu, yu, zu)为无人机质心在无人机坐标系下实时坐标,(xg, yg, zg)为无人机质心在地面坐标系的实时坐标,Lu, g为无人机坐标系相对于地面坐标系的转换系数,且满足:
$ {\mathit{\boldsymbol{L}}_{{\rm{u,g}}}} = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\theta {\rm{cos}}\psi }&{{\rm{sin}}\theta {\rm{sin}}\phi {\rm{cos}}\psi - {\rm{cos}}\phi {\rm{sin}}\psi }&{{\rm{sin}}\theta {\rm{cos}}\phi {\rm{cos}}\psi + {\rm{sin}}\phi {\rm{sin}}\psi }\\ {{\rm{cos}}\theta {\rm{sin}}\psi }&{{\rm{sin}}\theta {\rm{sin}}\phi {\rm{sin}}\psi - {\rm{cos}}\phi {\rm{cos}}\psi }&{{\rm{sin}}\theta {\rm{cos}}\phi {\rm{sin}}\psi + {\rm{sin}}\phi {\rm{cos}} \psi }\\ { - {\rm{sin}}\theta }&{{\rm{cos}}\theta {\rm{sin}}\phi }&{{\rm{cos}}\theta {\rm{cos}}\phi } \end{array}} \right] $
(4) 式中, θ, ϕ, ψ为无人机的三轴姿态角;(3)式为地面坐标运动方程,其中,${F_{{\rm{sum}}}} = \sum\limits_1^4 b \mathit{\Omega }_i^2$, b为旋翼电机的升力系数,Ωi为旋翼电机的转速,i为1号~4号电机;K={k1 k2 k3},分别为无人机在地面坐标系x轴、y轴、z轴3轴的空气阻力系数,综上可得,在地面坐标系下,无人机运动方程为:
$ \left[ {\begin{array}{*{20}{c}} {{{\ddot x}_{\rm{g}}}}\\ {{{\ddot y}_{\rm{g}}}}\\ {{{\ddot z}_{\rm{g}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{\mathit{\boldsymbol{F}}_{{\rm{sum}}}}}}{m}({\rm{sin}}\theta {\rm{cos}}\phi {\rm{cos}}\psi + {\rm{sin}}\phi {\rm{sin}}\psi ) - \frac{{{k_1}}}{m}{{\dot x}_{\rm{g}}}}\\ { - \frac{{{\mathit{\boldsymbol{F}}_{{\rm{sum}}}}}}{m}({\rm{sin}}\theta {\rm{cos}}\phi {\rm{sin}}\psi - {\rm{sin}}\phi {\rm{cos}}\psi ) - \frac{{{k_2}}}{m}{{\dot y}_{\rm{g}}}}\\ {\mathit{\boldsymbol{g}} - \frac{{{\mathit{\boldsymbol{F}}_{{\rm{sum}}}}}}{m}{\rm{cos}}\theta {\rm{cos}}\phi - \frac{{{k_3}}}{m}{{\dot z}_{\rm{g}}}} \end{array}} \right] $
(5) -
四旋翼无人机的控制参量主要是用来控制无人机的四旋翼电机,给无人机提供特定方向的动力,因此无人机的欠输入参量与无人机的飞行动力紧密相关。由于四旋翼无人机的质心即为其中心,所以其姿态转动可以视为刚体绕质心的定点转动。根据转动力学定理可知,地面坐标系下四旋翼无人机的力学方程[13-15]如下式所示:
$ \frac{{{\rm{d}}\mathit{\boldsymbol{L}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}(\mathit{\boldsymbol{I\omega }})}}{{{\rm{d}}t}} = {\left( {\frac{{{\rm{d}}\mathit{\boldsymbol{L}}}}{{{\rm{d}}t}}} \right)_{\rm{u}}} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{M}} $
(6) 式中, L为角动量,I为转动惯量,ω为角速度,M为无人机的外力矩, (dL/dt)u为无人机质心坐标系下的角动量的变化率。
又因,,,其中, Ix, Iy, Iz为机体坐标系下xyz 3轴向地面坐标系xyz 3轴的转动惯量。所以有:
$ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{l}} {{M_x}}\\ {{M_y}}\\ {{M_z}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_x}\ddot \theta ({I_z} - {I_y})\dot \phi \dot \psi }\\ {{I_y}\ddot \phi ({I_x} - {I_z})\dot \psi \dot \theta }\\ {{I_z}\ddot \psi ({I_y} - {I_x})\dot \theta \dot \phi } \end{array}} \right] $
(7) 无人机转动过程中,作用力主要有旋翼产生的动力和空气阻力。由牛顿定理和欧拉转动定理可知,“十”型四旋翼的转动力矩τ如下式所示:
$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\tau }} = ({\mathit{\boldsymbol{\tau }}_F} - {\mathit{\boldsymbol{\tau }}_{\rm{a}}}) = \left[ {\begin{array}{*{20}{c}} {{\tau _\theta }}\\ {{\tau _\phi }}\\ {{\tau _\psi }} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {Lb({\varOmega _3}^2 - {\varOmega _1}^2) - {\tau _{{\rm{a}},x}}}\\ {Lb({\varOmega _4}^2 - {\varOmega _2}^2) - {\tau _{{\rm{a}},y}}}\\ {d({\varOmega _1}^2 - {\varOmega _2}^2 + {\varOmega _3}^2 - {\varOmega _4}^2) - {\tau _{{\rm{a}},z}}} \end{array}} \right] \end{array} $
(8) 式中, L为旋翼中心距质心的距离,τa(τa, x, τa, y, τa, z)为空气阻力力矩, τF为动力阻力力矩。
继而可得十字型无人机的角运动方程如(9)式所示,考虑到四旋翼无人机飞行速度较小,受到空气阻力作用也较小,可将空气阻力忽略,得到(10)式:
$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{I_x}\ddot \theta + ({I_z} - {I_t})\dot \phi \dot \psi }\\ {{I_y}\ddot \phi + ({I_x} - {I_z})\dot \psi \dot \theta }\\ {{I_z}\ddot \psi + ({I_y} - {I_x})\dot \theta \dot \phi } \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {Lb({\varOmega _3}^2 - {\varOmega _1}^2) - {\tau _{{\rm{a}},x}}}\\ {Lb({\varOmega _4}^2 - {\varOmega _2}^2) - {\tau _{{\rm{a}},y}}}\\ {d({\varOmega _1}^2 - {\varOmega _2}^2 + {\varOmega _3}^2 - {\varOmega _4}^2) - {\tau _{{\rm{a}},z}}} \end{array}} \right] \end{array} $
(9) $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\ddot \theta }\\ {\ddot \phi }\\ {\ddot \psi } \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {Lb({\varOmega _3}^2 - {\varOmega _1}^2)/{I_x} - \dot \phi \dot \psi ({I_z} - {I_y})/{I_x}}\\ {Lb({\varOmega _4}^2 - {\varOmega _2}^2)/{I_y} - \dot \psi \dot \theta ({I_x} - {I_z})/{I_y}}\\ {d({\varOmega _1}^2 - {\varOmega _2}^2 + {\varOmega _3}^2 - {\varOmega _4}^2)/{I_z} - \dot \theta \dot \phi ({I_y} - {I_x})/{I_z}} \end{array}} \right] \end{array} $
(10) 设无人机的四输入控制量的力矩分别为俯仰力矩μ1、滚转力矩μ2、偏航力矩μ3、爬升力矩μ4,可得下式:
$ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\mu }}_1} = Lb({\varOmega _3}^2 - {\varOmega _1}^2)}\\ {{\mathit{\boldsymbol{\mu }}_2} = Lb({\varOmega _4}^2 - {\varOmega _2}^2)}\\ {{\mathit{\boldsymbol{\mu }}_3} = d({\varOmega _1}^2 - {\varOmega _2}^2 + {\Omega _3}^2 - {\Omega _4}^2)}\\ {{\mathit{\boldsymbol{\mu }}_4} = b({\varOmega _1}^2 - {\varOmega _2}^2 + {\varOmega _3}^2 + {\varOmega _4}^2)} \end{array}} \right. $
(11) 忽略空气阻力的作用,由(5)式、(10)式可得无人机的六自由度系统方程[16]如下式所示:
$ \left\{ {\begin{array}{*{20}{l}} {\ddot \theta = {\mathit{\boldsymbol{\mu }}_1}/{I_x} - \dot \phi \dot \psi ({I_z} - {I_y})/{I_x}}\\ {\ddot \phi = {\mathit{\boldsymbol{\mu }}_2}/{I_y} - \dot \psi \dot \theta ({I_x} - {I_z})/{I_y}}\\ {\ddot \psi = {\mathit{\boldsymbol{\mu }}_3}/{I_z} - \dot \theta \dot \phi ({I_y} - {I_x})/{I_z}}\\ {{{\ddot x}_{\rm{g}}} = - \frac{{{\mathit{\boldsymbol{\mu }}_4}}}{m}({\rm{sin}}\theta {\rm{cos}}\phi {\rm{cos}}\psi + {\rm{sin}}\phi {\rm{sin}}\psi )}\\ {{{\ddot y}_{\rm{g}}} = - \frac{{{\mathit{\boldsymbol{\mu }}_4}}}{m}({\rm{sin}}\theta {\rm{cos}}\phi {\rm{sin}}\psi - {\rm{sin}}\phi {\rm{cos}}\psi )}\\ {{{\ddot z}_{\rm{g}}} = - \frac{{{\mathit{\boldsymbol{\mu }}_4}}}{m}{\rm{cos}}\theta {\rm{cos}}\phi + \mathit{\boldsymbol{g}}} \end{array}} \right. $
(12) 无人机实际飞行中,通常只涉及俯仰飞行和偏航飞行,特殊条件下才伴有滚转飞行,因此对滚转角暂不进行研究。本文中基于视觉图像的无人机飞姿控制研究核心内容就是:通过初始状态下无人机的定速定向飞行,识别已知运动状态的特定地面合作目标,通过图像中目标像点位移情况,推算无人机的飞姿信息和高度,并利用无人机航迹与合作目标轨迹的夹角等信息,得出无人机完成跟踪或降落过程所需要的飞控参量。从前面可知,“十”型四旋翼无人机初始高度H0定向飞行时,质心坐标系与地面坐标系只存在一个夹角也即俯仰角θ0,由于此时无人机没有进行滚转飞行即ϕ0=0,因此此时无人机航迹与合作目标的航迹的像平面夹角也即偏航角ψ0,无人机要完成跟踪或降落功能,就需要对航迹进行修正,修正量即为H0, θ0, ψ0。由参考文献[17]和参考文献[18]可知,θn=${array}{l} \arctan \left[ {\Delta a_n^*{H_n}/(fa)} \right], {{\dot \theta }_n} = \left( {{\theta _n} - {\theta _{n - 1}}} \right)/\Delta t, {{\ddot \theta }_n} = \left( {{{\dot \theta }_n} - } \right. \left. {{{\dot \theta }_{n - 1}}} \right)/\Delta t, {\psi _n} = \arctan \left[ {\left( {a_{ni}^*\;{\rm{d}}y} \right)/\left( {a_{nj}^*\;{\rm{d}}x} \right)} \right], {{\dot \psi }_n} = \\ \left( {{\psi _n} - {\psi _{n - 1}}} \right)/\Delta t, {{\ddot \psi }_n} = \left( {{{\dot \psi }_n} - {{\dot \psi }_{n - 1}}} \right)/\Delta t {array}$,其中, a为合作目标外边长度,an*为n时刻外边a的像素值,Δan*为两条相对外边像的长度差,ani*, anj*分别为an*在像素坐标的行宽和列宽。所以基于视觉图像的四旋翼无人机四输入控制量为:
$ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\mu }}_1} = Lb({\varOmega _3}^2 - {\varOmega _1}^2) = \frac{{({\theta _n} + {\theta _{n - 2}} - 2{\theta _{n - 1}})}}{{{{(\Delta t)}^2}}}{I_x}}\\ {{\mathit{\boldsymbol{\mu }}_2} = Lb({\varOmega _4}^2 - {\varOmega _2}^2) = \frac{{({\theta _n} + {\theta _{n - 1}})({\psi _n} - {\psi _{n - 1}})}}{{{{(\Delta t)}^2}}}({I_x} - {I_z})}\\ {{\mathit{\boldsymbol{\mu }}_3} = d({\varOmega _1}^2 - {\varOmega _2}^2 + {\Omega _3}^2 - {\Omega _4}^2) = \frac{{{\psi _n} + {\psi _{n - 2}} - 2{\psi _{n - 1}}}}{{{{(\Delta t)}^2}}}{I_z}}\\ {{\mathit{\boldsymbol{\mu }}_4} = b({\varOmega _1}^2 + {\varOmega _2}^2 + {\varOmega _3}^2 + {\varOmega _4}^2) = \frac{{(fa/a_n^* - {H_0} - \mathit{\boldsymbol{g}})m}}{{{\rm{cos}}{\theta _n}}}} \end{array}} \right. $
(13) -
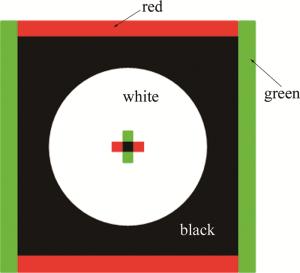
设计了一种具有方向引导功能的多形状组合彩色合作目标,如图 5所示。红色、绿色引导带指示目标移动方向,黑色、白色图形提升目标与周围环境的识别率,圆形、正方形能够提供较为精确地方向和角度信息。根据合作目标独有的灰度特征、几何特征、颜色特征、以及点特征,先后经灰度变换、色相、饱和度明度(hue saturation value, HSV)色彩变换、以及Hu不变距匹配等方法,从机载相机拍摄的连续帧实时图像中准确识别出合作目标,并获取有关的位姿信息。如位移像素xu, yu, zu,外边像素an*,外边像素差Δan*等。同时,在无人机低空和超低空飞行时,颜色导引带可以快速提供准确的目标方向信息,便于无人机快速的识别和跟踪合作目标, 如图 6所示。
-
根据同物不同时像平面像素变化情况,利用无人机物像关系式、质心运动方程和地面坐标方程等,计算出地面坐标系下合作目标相对于无人机的3轴位移变量,再结合第2.3节中θn和ψn的公式以及ϕ0=0,得出无人机的3轴角度,相对时间进行求导,得出无人机三轴线速度信息{$\dot x, \dot y, \dot z$}和角速度信息{$\dot \theta , \dot \phi , \dot \psi $},进而获得无人机的实时高度、坐标转换矩阵Lu, g等。
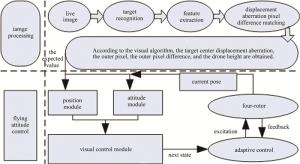
使用基于视觉图像的无人机飞行控制算法如图 7所示。主要通过提取图像中目标特征点的位移信息,获取无人机的实时位姿信息,利用前后两个固定时间段位姿信息对时间的导数,得到无人机的速度信息。以当前时刻无人机与合作目标的位姿差信息,作为下一时刻加速度的控制矢量,直至在地面坐标系下无人机与合作目标的位姿信息差为0,此时无人机完成稳定跟踪功能[19-20],如下式所示:
$ \left\{ {\begin{array}{*{20}{l}} {\Delta {x_{\rm{g}}} = \frac{{\Delta {O_{\rm{c}}}^ * \cdot a}}{{a_n^*}}{\rm{cos}}\theta {\rm{cos}}\psi }\\ {\Delta {y_{\rm{g}}} = \frac{{\Delta {O_{\rm{c}}}^ * \cdot a}}{{{a_n}^ * }}{\rm{cos}}\theta {\rm{sin}}\psi }\\ {\Delta {z_{\rm{g}}} = \frac{{({a_n}^ * - {a_{n - 1}}^ * )}}{f}{\rm{sin}}\theta } \end{array}} \right. $
(14) 式中, ΔOc*为合作目标当前时刻与前一时刻的位移像差。同理,当合作目标中心与无人机质心在像平面保持重合或近似重合时,无人机即可完成自主降落功能。
从(14)式可知,当Δxg, Δyg, Δzg三者出现数值时,表示无人机完成搜索识别阶段,当Δxg, Δyg两者为零时,无人机完成稳定跟踪阶段,当Δxg, Δyg, Δzg都为零时,即完成自主降落功能。
-
为了进一步验证基于视觉图像的无人机控制算法的科学性和可行性,利用MATLAB软件进行了仿真实验,主要研究不同高度不同速度下无人机完成识别跟踪及降落过程的时效性和精准性。
-
表 1中为仿真实验的部分参量。
Table 1. Parameters of simulation experiment
symbol definition size m UAV quality 1kg g gravity acceleration 9.81m/s2 L rotor distance from the center of mass 0.15m H0 UAV height 20m Δt position resolution interval 0.1s vc cooperation target speed 1m/s a target outside 1.2m d inner cross length 0.2m f camera focal length 0.02m dx cell width 6×10-6 m dy cell length 6×10-6 m Fsum, 0 rotor initial lift 9.81N θ0 initial pitch angle 0 ϕ0 initial roll angle 0 ψ0 initial yaw angle π/4 Ix x-axis moment of inertia 5.4×10-3kg·m2 Iy y-axis moment of inertia 5.4×10-3kg·m2 Iz z-axis moment of inertia 1.2×10-3kg·m2 -
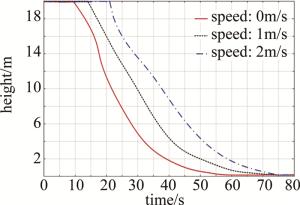
本文中无人机控制系统分为位置控制器和姿态控制器,利用同物不同时像素位移情况,解算出无人机与合作目标的位姿关系作为当前时刻实测值,通过基于视觉图像的无人机飞行控制算法,解算无人机与合作目标位姿差作为下一时刻的期望值,根据期望值不断调整位置与姿态两个控制器,进而控制不同时刻的实测值,当实测值逐渐降为0时,即完成自主降落功能。通过研究同高异初速条件下无人机与合作目标的高度和中心位距离随时间的变换关系,验证算法的可行性和精确性,实验结果如图 8和图 9所示。
通过仿真实验发现,无人机初速对跟踪、靠近、着陆3个阶段的影响是不尽相同的。高度方面:跟踪阶段,初速对合作目标的识别效率有一定影响,初速为0时,识别时间越短,主要因为悬停时姿态角为0,便于无人机搜索识别。靠近阶段:初速小时,无人机z轴方向分量也就小,高度变化就慢,随着期望位姿信息的逐渐变大,z轴方向分量也随之变大,高度变换也随之加大;初速大时,无人机z轴方向分量也就大,高度变化就快,随着期望位姿信息的逐渐变小,z轴方向分量也随之变小,高度变化也随之减小,达到最大值时保持不变,降落曲线则表现为类直线。着陆阶段,由于经过前两个阶段的调整控制,无人机的状态基本一致,所以初速对着陆阶段没有影响,高度随z轴速度一致逐渐减为0。距离差方面:跟踪阶段,中心距离都是逐渐增大,初速越大,距离越大,合作目标运动方向分量大小相同后达最大值。靠近阶段,距离越小,位姿信息变化的期望值越小,距离变化就越缓;距离越大,位姿信息变化的期望值越大,距离变化就越剧烈,同理达到最大值时保持不变直至进入着陆阶段。着陆阶段,初速对距离差同样没有影响,距离随着无人机的降落逐渐减为0。
-
针对无人机跟踪或降落过程中信源易被干扰、环境感知较差问题,利用视觉图像的无源性、实时性特性,在同物不同时物像像素变化关系的基础上,根据牛顿力学定理与刚体转动定理,通过无人机位姿信息的提取与控制参量的转换,确立了无人机六自由度信息与四输入参量之间的关系,提出了基于视觉图像的无人机飞行控制算法,并进行了仿真实验。实验结果表明,所提出的控制系统算法在识别跟踪目标后,可以独立完成无人机自主降落功能,克服了无线电信源易干扰有延时的不足,且动态性能良好。该算法的成熟与应用将有助于真正实现无人机自主化和智能化。
基于视觉图像的四旋翼无人机飞行控制研究
Research on flight control of quadrotor UAV based on visual image
-
摘要: 为了利用视觉图像中信息的无源性、实时性以及机载控制器的自创性等特性,解决无人机信源易干扰、有延时、受制约的问题,分析了“十”字型四旋翼无人机的动力结构、控制原理以及无人机飞行过程中位姿方程、动力方程之间的相互关系,完成了四旋翼无人机六自由度信息和飞行控制四元素输入信息之间的转换,设计了基于合作目标匹配的无人机视觉图像自主控制算法。结果表明,在实测值为零时,即可完成自主降落功能。该算法可以实现简单环境下四旋翼无人机的自主降落。这一研究对无人机的自主化、智能化发展具有一定的帮助作用。Abstract: In order to make full use of the characteristics of the passiveness, real-time nature of the information in the visual image, and the self-creation of the on-board controller, to effectively solve the problems of easy interference, delay, and constraints of the drone signal source, the "十" dynamic structure and control principle of the quad-rotor unmarned aerial vehide(UAV) and the relationship between the posture equation and the dynamic equation during the flight of the UAV were analyzed. The conversion between the six-degree-of-freedom information of the quad-rotor UAV and the four elements of flight control information were completed. An autonomous control algorithm for unmanned aerial vehicle vision images based on cooperative target matching was then designed. The computer simulation verification proves that the algorithm can realize the autonomous landing of a four-rotor drone in a simple environment. This research will help the autonomous and intelligent development of drones.
-
Key words:
- physical optics /
- visual image /
- pose solution /
- autonomous landing /
- unmarned aerial vehide
-
Table 1. Parameters of simulation experiment
symbol definition size m UAV quality 1kg g gravity acceleration 9.81m/s2 L rotor distance from the center of mass 0.15m H0 UAV height 20m Δt position resolution interval 0.1s vc cooperation target speed 1m/s a target outside 1.2m d inner cross length 0.2m f camera focal length 0.02m dx cell width 6×10-6 m dy cell length 6×10-6 m Fsum, 0 rotor initial lift 9.81N θ0 initial pitch angle 0 ϕ0 initial roll angle 0 ψ0 initial yaw angle π/4 Ix x-axis moment of inertia 5.4×10-3kg·m2 Iy y-axis moment of inertia 5.4×10-3kg·m2 Iz z-axis moment of inertia 1.2×10-3kg·m2 -
[1] ZHANG M, ZHAO Y, BU Sh H, et al. Autonomous precision landing system for UAV based on hierarchical identification[J]. Acta Aeronautica Sinica, 2018, 39(10):213-221(in Chinese). [2] YANG J, WANG R. Road control of UAV track based on acceleration input[J]. Automation Technology and Application, 2015, 34(12):15-19(in Chinese). [3] YE G Q. Study on key technologies of feature selection image visual servo[D]. Guangzhou: South China University of Technology, 2017: 34-57(in Chinese). [4] LIU F, WANG H J, HUANG G W, et al. Target tracking algorithm for UAV based on adaptive depth network[J]. Acta Aeronautica Sinica, 2018, 40(3):321-329(in Chinese). [5] DOU J X, KONG X X, WEN B Ch. Fuzzy auto-disturbance rejection attitude control and stability analysis of quadrotor UAV[J]. Journal of Chinese Inertial Technology, 2015, 23(6):824-830(in Chinese). [6] CHEN J. Research on dynamic modeling and control technology of four-rotor unmanned aerial vehicle[D]. Nanjing: Nanjing University of Science and Technology, 2016, 42-56(in Chinese). [7] WANG R, LIU J K. Trajectory tracking control of a 6-DOF quadrotor UAV with input saturation via backstepping[J]. Journal of the Franklin Institute, 2018, 355(7):3288-3309. doi: 10.1016/j.jfranklin.2018.01.039 [8] JIA P Y, PENG X D, ZHOU W G. Research on autonomous moving and falling method of quadrotor UAV[J]. Journal of Computer Science, 2017, 44(s2):520-523(in Chinese). [9] FANG X, LIU J K. Dynamic surface control of four-rotor UAV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(8):1777-1784(in Chinese). [10] KHALIFA A, FANNI M. A new quadrotor manipulation system: Modeling and point-to-point task space control[J]. International Journal of Control, Automation and Systems, 2017, 15(3):1434-1446. [11] LIU J T, WU W H, LI J. Moving target tracking control of four-rotor UAV without speed measurement[J]. System Engineering and Electronics, 2017, 39(2):369-375(in Chinese). [12] AMIRKHANI A, SHIRZADEH M, PAPAGEORGIOU E I, et al. Visual-based UAV control by means of fuzzy cognitive maps[J]. ISA Transactions, 2016, 60(1):128-142. [13] ZHANG Sh G. An attitude tracking control of quadrotor UAV based on neural network[D]. Harbin: Harbin Institute of Technology, 2017: 30-45(in Chinese). [14] GOODARZI F A, LEE D, LEE T. Geometric control of a quadrotor UAV transporting a payload connected via flexible cable[J]. International Journal of Control Automation & Systems, 2015, 13(6):1486-1498. [15] WANG X J, WAN Z J, WANG X, et al. Real-time autonomous vision localization of UAV ground targets[J]. Infrared and Laser Engineering, 2014, 43(2): 615-619(in Chinese). [16] SHAO X, TAO J W. Study on static target location based on mono-cular vision[J]. Acta Photonica Sinica, 2016, 45(10): 1012003(in Chinese). doi: 10.3788/gzxb20164510.1012003 [17] DENG B W. Design and implementation of four-rotor UAV flight control system[D]. Changsha: National University of Defense Technology, 2015: 42-53(in Chinese). [18] SUO W K, HU W G, ZHANG Y, et al. Study on visual positioning method of autonomous landing process of UAV[J]. Laser Technology, 2019, 43(5):371-376(in Chinese). [19] HUANG N N, LIU G X, ZHANG Y Zh, et al. Visual navigation algorithm for drones[J].Infrared and Laser Engineering, 2016, 45(7):0726005(in Chinese). doi: 10.3788/irla201645.0726005 [20] LI Zh P, ZHANG Y G, AI Y, et al. Laser tracking and wireless energy supply system for drones[J]. Laser Technology, 2018, 42(3): 22-26(in Chinese). -


 网站地图
网站地图

 下载:
下载: