-
等效热焦距参量是评估高能固体激光器热效应的核心参量[1-2]。随着固体激光器输出功率的提高,激光材料热效应愈加明显,等效热焦距参量的测量也逐渐受到重视[3-5]。基于泰伯-莫尔条纹长焦距测量技术是广泛应用于长焦距光学元件焦距参量精确测量的方法,也是实现等效热焦距参量精确测量的重要途径之一[6]。它的基本原理是一束平行光束连续通过两个相同周期的Rochi光栅,利用一个光栅的衍射自成像与第2个光栅的叠加形成莫尔条纹,通过莫尔条纹倾角测得被测元件焦距值。此方法具有测量范围大、测量精度高、光路简单、操作方便等优点[7-9]。莫尔条纹倾角求解是该技术的核心之一,是测量系统测量精度和测量速度的主要影响因素。其中莫尔条纹倾角测量误差引起的焦距误差占整个焦距测量误差的90%[10]。为提高莫尔条纹倾角的求解精度,浙江大学HOU等人[11]提出了精确计算莫尔条纹倾角的傅里叶迭代算法;YU在他的基础上提出了基于信息熵的迭代算法[12]。这两种方法均通过傅里叶变换求取莫尔条纹频谱,并通过迭代运算逐步逼近1级频谱的精确坐标,进而求解莫尔条纹倾角。算法突破数字图像像素的限制,显著提高莫尔条纹的测量精度,倾角求解精度可达10-4rad量级。
迭代运算的引入在提高测量精度的同时也降低了测量速度,当迭代次数为10次时,采用常规配置计算机完成一次测量用时15s左右;基于信息熵的迭代算法在迭代20次时完成一次测量用时47s[12]。对于光学元件焦距的测量,测量时间不是主要问题,但激光材料热效应等效热焦距参量随抽运时间快速变化,单次测量时间过长将无法反应热效应的变化过程,需要以大于1Hz的频率进行测量[13-15]。为提高激光材料热效应等效热焦距参量的测量速度,本文中在对频域迭代法测量速度影响因素分析的基础上,基于迭代运算坐标位置的相似性,将离散傅里叶变换公式进行变形,将频谱坐标中包含小数值坐标点进行公共项分离,公共部分采用傅里叶变换系数进行滤波,不同部分在提取相似项的基础上进行组合运算,将2维条纹图像降为1维数据进行处理,整体上减少运算复杂度。同时坐标点的分离将不同部分限定在极小的可知范围,极大地方便了查表运算和位运算的采用,提高了算法执行效率。编写软件,通过实验验证了快速求解算法的可行性和运算速度,结果表明,在保证测量精度的前提下完成一次测量耗时为0.4s,很大地提高了莫尔条纹倾角的求解速度,满足了等效热焦距参量测量对测量速度的需求。
-
莫尔条纹是由两块等间隔排列的直线族或曲线族叠加产生的周期性条纹图像。在基于泰伯-莫尔条纹长焦距测量技术中由一个光栅的衍射自成像与第2个光栅的叠加形成,其倾角是莫尔条纹与图像坐标轴的夹角,直接反映被测元件的焦距值。在莫尔条纹频谱域中,条纹倾角与其频谱±1级的连线存在π/2的夹角,因此, 莫尔条纹倾角的求解可通过求解频谱的±1级坐标求解。对莫尔条纹图像进行傅里叶变换即可得到莫尔条纹频谱。但CCD采集到的莫尔条纹图像为数字图像,受CCD分辨率的限制,仅进行快速离散傅里叶变换只能求解整数像素点坐标,若条纹数量为N,则算法测量精度仅为(1/N)rad,测量精度无法达到要求。
-
为方便莫尔条纹倾角求解,一般CCD采集的莫尔条纹行列方向像素相同,设为M,则可采用离散傅里叶变换公式在整数点坐标的基础上求解单个像素内含分数点坐标(u, v)的频谱值。将坐标点的求解精度提高到亚像素级别,进而可将莫尔条纹倾角的求解精度提高100倍左右。
$ F\left( {u, v} \right) = \frac{1}{{{M^2}}}\sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{M - 1} {f\left( {x, y} \right)} } \times \exp \left[ { - {\rm{i}}2{\rm{ \mathsf{ π} }}\left( {\frac{{ux + vy}}{M}} \right)} \right] $
(1) 式中,f(x, y)为条纹图像灰度值,F(u, v)为条纹图像频谱。
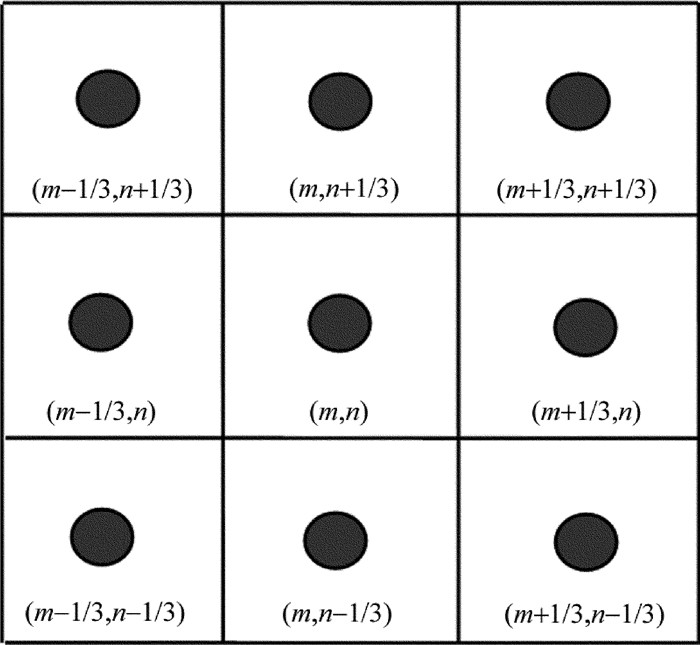
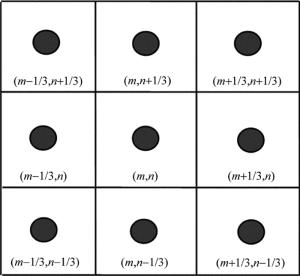
由于坐标值(u, v)存在小数部分,无法采用快速傅里叶变换算法,运用(1)式计算像素内各位置的频谱就需要庞大的计算量,计算速度必然很慢。莫尔条纹图像是按一定规律分布的标准余弦图像,由于系统误差的存在,其频谱图的+1级在整像素内是按以最大值为中心的2维高斯分布。这个特点说明可以通过迭代逐渐逼近的方法找到其最大值,从而减少运算量。基于此频域迭代算法采用像素分割,比较定位的方法逼近最大值。首先对莫尔条纹进行快速傅里叶变换得到其频谱图,确定频谱图的+1级坐标点,也即对频域的+1最大值进行整数像素点初定位,得到其序列值,设其序列值为(m, n);然后以频域的+1级点为中心,把最大值点所在像素按九宫格进行分割,九宫格像素分割法如图 1所示。
九宫格内各宫格的坐标值为:(m+1/3, n+1/3),(m+1/3, n),(m+1/3, n-1/3),(m, n+1/3),(m, n),(m, n-1/3),(m-1/3, n+1/3),(m-1/3, n),(m-1/3, n-1/3)。采用(1)式求解各宫格中心处的频谱值,比较各个频谱值,确定最大值的坐标值(u0, v0);重复上述方法,以每次得到的最大值的坐标值为中心,按步长1/3k进行九宫格分割完成第k次迭代运算,再求解最大值,这样经过多次分割后逐渐逼近+1级频谱最大值,达到提高测量精度的目的。算法覆盖了整像素内的整个区域,也相当于求解了整个区域频谱值。
-
采用频域迭代法完成莫尔条纹倾角测量,当迭代10次需要计算90个频谱值,减少了很多次计算,但由于最大值坐标点包含小数部分,频谱功率值计算只能采用指数运算,算法执行效率很低,完成一次测量仍然需要花费十几秒的时间。
为进一步提高莫尔条纹倾角求解速度,本文中从频谱值的求解上寻找方法。分析频域迭法频谱值的计算过程知,9个坐标点均是由上次迭代频谱值最大值点坐标(u0, v0)与步长1/3k的和差,因此对于本次迭代运算,上次迭代最大值点坐标是公共部分,步长为不同部分。将每一个频谱点坐标(u, v)写为u=u0+uk, v=v0+vk,其中(u0, v0)为上次迭代频谱值最大值点坐标,(uk, vk)为本次运算的迭代步长,因此可将(1)式改写为:
$ \begin{array}{l} F\left( {u, v} \right) = \frac{1}{{{M^2}}}\sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{M - 1} {f\left( {x, y} \right)} } \times \\ \exp \left[ { - {\rm{i}}2{\rm{ \mathsf{ π} }}\left( {\frac{{{u_0}x + {v_0}y}}{M}} \right)} \right] \times \\ \exp \left[ { - {\rm{i}}2{\rm{ \mathsf{ π} }}\left( {\frac{{{u_k}x + {v_k}y}}{M}} \right)} \right] \end{array} $
(2) 若设:
$ \left\{ {\begin{array}{*{20}{c}} {f'\left( {x, y} \right) = f\left( {x, y} \right)\exp \left[ { - {\rm{i}}2{\rm{ \mathsf{ π} }}\left( {\frac{{{u_0}x + {v_0}y}}{M}} \right)} \right]}\\ {w\left( {x, y} \right) = \exp \left[ { - {\rm{i}}2{\rm{ \mathsf{ π} }}\left( {\frac{{{u_k}x + {v_k}y}}{M}} \right)} \right]} \end{array}} \right. $
(3) 则(2)式可变为:
$ F\left( {u, v} \right) = \frac{1}{{{M^2}}}\sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{M - 1} {f'\left( {x, y} \right)w\left( {x, y} \right)} } $
(4) 基于(4)式对迭代运算中各点频谱值进行求解,f′(x, y)为一次迭代公共部分,采用傅里叶变换指数项对莫尔条纹图像进行滤波运算完成。迭代运算中,w(x, y)的坐标点(uk, vk)分别为(1/3k, 1/3k), (1/3k, 0), (1/3k, -1/3k), (0, 1/3k), (0, 0), (0, -1/3k), (-1/3k, 1/3k), (-1/3k, 0), (-1/3k, -1/3k),其中k为迭代次数。对于坐标点(1/3k, 1/3k), (-1/3k, -1/3k),若x+y相同,则w(x, y)相等,因此可先计算相同点f′(x, y)的和,将M×M 2维数据降为长度为2M的1维数据参与计算。同理,对于(1/3k, 0), (-1/3k, 0)可先计算x相同点f′(x, y)的和;对于(0, 1/3k), (0, -1/3k)可先计算y相同点f′(x, y)的和;对于(1/3k, -1/3k), (-1/3k, 1/3k)可先计算x-y相同点f′(x, y)的和,将M×M 2维数据降为4组1维数据参与计算。因此(4)式可变为:
$ \left\{ {\begin{array}{*{20}{c}} {E\left( n \right) = \exp \left( { - {\rm{i2 \mathsf{ π} }}\frac{n}{{{3^k}M}}} \right)}\\ {F\left( {u, v} \right) = \frac{1}{{{M^2}}}\sum\limits_{n = 0}^{2M} {H\left( n \right)} \times E\left( n \right)} \end{array}} \right. $
(5) 式中, H(n)为f′(x, y)满足坐标关系的条纹灰度值和。E(n)为长度为2M的指数项,对于每次迭代运算E(n)的值固定,可建立数据表,在计算F(u, v)过程中采用查表运算和位运算,极大地提高了算法运算效率。
快速求解算法基于迭代运算坐标位置的相似性,将离散傅里叶变换公式进行变形,将频谱坐标分为公共项和不同部分,公共部分采用傅里叶变换系数进行滤波,不同部分在提取相似项的基础上进行组合运算,将2维条纹图像降为1维数据,同时坐标点的分离将不同部分限定在极小的可知范围,极大地方便了查表运算和位运算的采用。算法整体上提高了莫尔条纹倾角的求解速度。快速求解算法流程如图 2所示。步骤如下:(1)在测量开始前建立20次迭代运算中所有指数项E(n)的数据表;(2)对莫尔条纹图像进行快速傅里叶变换(fast Fourier transform, FFT),求解零频坐标(m0, n0)和+1级频谱整像素点坐标值(m, n);(3)代入整像素点坐标(m, n),求解一次迭代运算公共部分f′(x, y)的值,同时求解满足x+y, x, y, x-y相等坐标点f′(x, y)的值和H(n);(4)分别求解九宫格中各坐标点的频谱值,并求解频谱最大值的坐标(mk, nk);(5)代入坐标(mk, nk), 求解k+1次迭代运算公共部分f′(x, y)的值,重复步骤(3)和步骤(4),求解第n次迭代运算坐标点计算莫尔条纹倾角。
-
构建了仿真实验和等效热焦距测量实验,分别对快速求解算法的测量精度和测量速度进行验证。其中,通过仿真实验模拟不同角度莫尔条纹,采用传统频域迭代算法和快速求解算法对模拟莫尔条纹的倾角进行测量,三者进行对比验证快速求解算法的测量精度;通过等效热焦距测量实验采集莫尔条纹,对两种测量算法的测量速度进行对比,验证快速求解算法的测量速度,同时验证快速求解算法对激光材料热效应等效热焦距参量测量的适用性。
-
基于MATLAB软件构建了理想莫尔条纹模拟程序和算法仿真程序。模拟了倾角为5°, 15°, 30°, 45°, 60°, 75°, 85°, 90°的莫尔条纹,其中倾角为45°的模拟莫尔条纹如图 3所示。
分别采用传统频域迭代算法和快速求解算法对莫尔条纹倾角进行求解,迭代10次,测量结果如表 1所示。
Table 1. Results with different algorithms
simulate angle/(°) traditional algorithm/(°) fast algorithm/(°) 5 5.001 5.001 15 15.002 15.002 30 30.001 30.001 45 45.000 45.000 60 59.999 59.999 75 74.998 74.998 85 85.001 85.001 90 89.999 89.999 由表 1可知,传统算法和快速求解算法的测量结果完全一致,而且和模拟角度均小于0.002°。排除图像离散化过程引入的测量误差,两种算法均可精确求解莫尔条纹倾角,测量误差小于0.002°,证明了快速求解算法的测量精度。
-
采用实验室基于泰伯-莫尔条纹技术研制的长焦距测量仪对500J钕玻璃激光器激光材料热效应等效热焦距参量进行测量。测量算法以长焦距测量仪测量软件为基础,采用Visual Studio 2008编码实现,计算机为CPU Intel i3处理器(主频3.5GHz)及内存4GB的工控机。通过对比两种测量算法的测量时间验证快速求解算法的测量速度,并验证测量算法对等效热焦距参量的测量的有效性。CCD采集的莫尔条纹见图 4。
采集任意状态下12幅莫尔条纹图,采用传统频域迭代算法和快速求解算法对条纹倾角进行求解,测量时间如表 2所示。
Table 2. Measurement time results with different algorithms
number traditional algorithm/s fast algorithm/s 1 15.62 0.33 2 14.31 0.42 3 13.48 0.43 4 16.26 0.33 5 17.12 0.38 6 13.61 0.32 7 15.45 0.48 8 14.33 0.49 9 15.26 0.45 10 14.42 0.43 11 14.81 0.37 12 16.03 0.36 mean 15.0 0.4 由表 2可知,采用传统算法完成一次测量平均测量时间为15.0s,采用快速求解算法完成一次测量平均测量时间为0.4s,前者测量时间是后者的38倍,直接说明快速求解算法测量速度相对于传统算法得到很大的提高,验证了快速求解算法的测量速度。
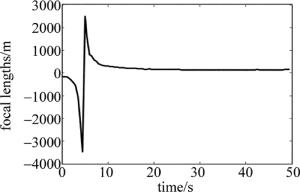
对实验室500J钕玻璃激光器在完成单次脉冲发射过程中激光材料热效应等效热焦距参量进行测量,测量间隔时间设置为0.5s,测量结果分布曲线见图 5。
由图 5可知,等效热焦距参量随时间快速变化,在脉冲发射后10s内,等效热焦距参量由-158.4m快速减小到-3400m然后变为2400m后再次快速减小到293.3m;10s以后等效热焦距变换相对缓慢,逐渐减小至130m后逐渐增大,到50s时增大到165m。从测量结果知,采用快速求解算法将测量时间间隔设置为0.5s得到的测量结果很好地反映了脉冲发射后等效热焦距参量的变化过程,从而证明了快速求解算法对激光材料热效应等效热焦距参量测量的适用性。
-
针对基于泰伯-莫尔条纹长焦距测量技术在测量激光材料热效应等效热焦距时对测量速度的需求,提出了一种莫尔条纹倾角快速求解算法,并对该算法的原理和流程进行了分析,整体上减少了算法复杂度,提高了莫尔条纹倾角的测量速度。建立了仿真实验,通过与模拟倾角和传统测量算法测量结果进行对比验证了快速求解算法的测量精度。建立物理实验,采用相同配置计算机,在保证测量精度的前提下传统测量算法平均测量时间为15s,快速求解算法的平均测量时间为0.4s,测量速度提高了38倍,证明了该算法的测量速度。对实验室500J钕玻璃激光器在完成单次脉冲发射过程中激光材料热效应等效热焦距参量进行了测量,测量结果证明快速求解算法满足等效热焦距参量的测量需求。
莫尔条纹倾角快速求解算法及应用
Fast algorithm for solving Moiré fringe angle and its application
-
摘要: 为了满足基于泰伯-莫尔条纹长焦距测量技术在测量激光材料热效应等效热焦距时对测量速度的需求,提出了一种莫尔条纹倾角快速求解算法。在对传统频域迭代法测量速度影响因素分析基础上,基于迭代运算坐标值相似性和离散傅里叶变换可分离性,将频谱值求解过程中包含小数值的坐标点进行公共项分离, 公共部分采用傅里叶变换指数项进行滤波,不同部分在提取相似项的基础上进行组合运算,将2维条纹图像傅里叶变换降为1维进行处理;同时相关指数项被限定在极小的可知范围,极大地方便了查表运算和位运算的采用。结果表明,采用相同配置计算机,在保证测量精度的前提下,将完成一次测量的测量时间从15s降低到0.4s,测量速度提高了38倍。该算法很好地满足了激光材料热效应等效热焦距参量快速测量的应用需求。Abstract: In order to meet the measurement speed requirement when measuring the equivalent thermal focal length of laser material thermal effect based on the Talbot interferometer, a fast algorithm for solving the Moiré fringe angle was proposed. The influence factors of measuring speed by traditional frequency iterative method were analyzed. Based on the similarity of the iterative computing coordinate value and the separability of discrete Fourier transform, the common points of the coordinate points containing decimal are separated from coordinate operation of the spectrum value solution process. The common is filtered by the Fourier transform exponential term, and the different parts are combined operation on the basis of extracting similarity. The 2-D image is reduced to 1-D, and the index items of different parts are limited to the minimal knowable range, which greatly facilitates the use of table-referring and bit-wise operation. The experimental results show that the measurement time with the same configuration computer is reduced from 15s to 0.4s on the premise of ensuring the measurement accuracy, and the measurement speed is increased by 38 times. The application requirement of the equivalent thermal focal length measurement was well satisfied.
-
Key words:
- measurement and metrology /
- angle solving /
- Fourier transform /
- Moiré fringe /
- thermal focus
-
Table 1. Results with different algorithms
simulate angle/(°) traditional algorithm/(°) fast algorithm/(°) 5 5.001 5.001 15 15.002 15.002 30 30.001 30.001 45 45.000 45.000 60 59.999 59.999 75 74.998 74.998 85 85.001 85.001 90 89.999 89.999 Table 2. Measurement time results with different algorithms
number traditional algorithm/s fast algorithm/s 1 15.62 0.33 2 14.31 0.42 3 13.48 0.43 4 16.26 0.33 5 17.12 0.38 6 13.61 0.32 7 15.45 0.48 8 14.33 0.49 9 15.26 0.45 10 14.42 0.43 11 14.81 0.37 12 16.03 0.36 mean 15.0 0.4 -
[1] ZOU J, ZHAO Sh Zh, YANG K J, et al. A simple method to determine the thermal focal length of solid-state lasers with rate equation[J]. Optics & Laser Technology, 2007, 39(4): 778-781. [2] HAN Y F, ZHANG R F, YANG H R, et al. Time-variable thermal effect in side-pump high power pulsed Nd:YAG laser[J]. High Power Laser and Particle Beams, 2015, 27(6): 24-31(in Chinese). [3] EL-AZAB J M, NADA Y S, MAIZE S M. Thermal focal length control in passively Q-switched end pulsed-pumped ceramics and single crystal Yb3+:YAG/ Cr4+:YAG microchip laser[J]. Nonlinear Optics, Quantum Optics, 2017, 48(2):113-122. [4] OU Q F, FENG G Y, LIU D P, et al. Simulation and experimental study on thermal effects of Nd:YAG lasers[J]. Laser Technology, 2002, 26(1): 15-16 (in Chinese). [5] EL-DAHER M S. Finite element analysis of thermal effects in diode end-pumped solid-state lasers[J]. Advances in Optical Technologies, 2017(2):1-15. [6] NAKANO Y, MURATA K. Talbot interferometry for measuring the focal length of a lens[J]. Applied Optics, 1985, 24(19):3162-3166. doi: 10.1364/AO.24.003162 [7] SINGH P, FARIDI M S, SHAKHER C. Measurement of focal length with phase-shifting Talbot interferometry[J]. Applied Optics, 2005, 44(9):1572-1576. doi: 10.1364/AO.44.001572 [8] ZHANG H, DAI H, FAN H Y, et al.Calibration and design of long focal length measurement instruments based on Talbot-Moiré effect[J].Laser Technology, 2019, 43(4):527-531(in Chinese). [9] CHEN H, HE Y, LI J X, et al.Measurement of long focal lengths with a double-grating interferometer[J]. Applied Optics, 2013, 52(27):6696-6702. doi: 10.1364/AO.52.006696 [10] HOU Ch L. Research on long focal length measurement system based on Talbot effect[D]. Hangzhou: Zhejiang University, 2005: 89-95 (in Chinese). [11] HOU Ch L, BAI J, HOU X Y, et al.The accurate measurement of angle based on Talbot effect of Ronchi grating[J].Optical Instruments, 2004, 26(1):11-14(in Chinese). [12] YU H L. The application and analysis of sub-pixel technology in processing moiré fringes in long focal length measurement system[D]. Hangzhou: Zhejiang University, 2013: 22-48 (in Chinese). [13] LUO K, WANG F, CHE Y, et al.Dynamic thermal focus length of solid state laser measured by polarization conversion[J].Infrared and Laser Engineering, 2016, 45(10):10170031(in Chinese). [14] DAI Q. Analysis of thermal effect in solid state lasers with heat capacity mode[J]. Optics and Precision Engineering 2008, 16(6) :1025-1030(in Chinese). [15] LI L, DONG W W, SHI P, et al. Thermal effect of diode bar side-pumped Nd:YAG slab[J]. Optics and Precision Engineering, 2008, 16(11):2120-2126(in Chinese). -


 网站地图
网站地图

 下载:
下载: