-
数字图像相关方法[1-4](digital image correlation,DIC)作为一种高效、实用的全场变形测量技术,已被广泛应用于实验力学等领域[5-8]。该方法通过对变形前后图像子区的唯一准确识别进行变形测量,被测物体表面需具备一定程度随机分布的灰度信息(或散斑),这些随机分布的灰度信息便是位移或变形的载体。国内外研究人员对DIC方法位移测量精度进行了大量研究[9-12],指出影响DIC方法位移测量精度的因素主要包括搜索算法、散斑图质量、亚像素插值方法、子区位移模式、光学镜头畸变等。VENDROUX等人[13]对牛顿-拉普森(Newton-Raphson, N-R)算法中的Hessian矩阵进行了近似处理,大大提高了该算法的计算效率。SCHREIER等人[14]研究了不同亚像素插值方法对位移测量精度的影响; 他们还曾分析了图像子区位移模式(形函数)对测量精度的影响。PAN等人[16]研究了不同的亚像素匹配算法在位移测量精度中的表现。WANG等人[17]研究了散斑尺寸对散斑图质量的影响。SATURU等人[18]研究了光学镜头的镜头畸变对DIC位移测量精度的影响。
在实际实验中,散斑图质量对位移测量精度有着十分重要的影响,在众多散斑图质量研究文献中,参考文献[17]和参考文献[19]中分别从散斑颗粒尺寸角度对散斑图质量进行了研究,并提出了最优散斑尺寸范围。参考文献[20]中从数字图像相关测量误差角度进行了理论分析,并提出了平均灰度梯度(mean intensity gradient,MIG)这一概念对散斑图质量进行评价。然而,在实际实验过程中,不同人或不同方法所制作出的散斑场的灰度分布千差万别,因此,仅从颗粒大小(部分人工制备的散斑图和物体表面的天然纹理并非具有明显的颗粒分布特征)角度或平均灰度梯度概念并不能准确表征散斑图质量。本文中通过对散斑图灰度信息分布形式进行分析,指出散斑图平均灰度2阶导数(mean intensity of second derivative,MISD)与散斑图灰度分布形式之间的关系,利用这一参量对散斑图质量进行评价并通过相关实验验证了该参量的有效性。
-
平均灰度梯度(用δf表示)这一概念是PAN等人[20]提出的对散斑图质量进行有效评价的全局参量,其公式如下:
$ \delta_{\mathrm{f}}=\frac{\sum\limits_{i=1}^{W} \sum\limits_{j=1}^{H}\left|\nabla f\left(x_{i j}\right)\right|}{W \times H} $
(1) 式中, W和H(以像素为单位)是图像的宽度和高度; $\left|\nabla f\left(x_{i j}\right)\right|=\sqrt{f_{x}\left(x_{i j}\right)^{2}+f_{y}\left(x_{i j}\right)^{2}} $是像素点xij处灰度梯度矢量的模, fx(xij)和fy(xij)分别为像素点xij在x和y两个方向的灰度导数, 其可利用梯度算子进行计算。
PAN等人的研究结果显示, 位移测量结果的均值误差和标准差均与散斑图的平均灰度梯度有关,散斑图具有高的平均灰度梯度对应较低的测量误差。对于散斑图而言,δf越大,对整个散斑图意味着该散斑图含有更多的信息量(或者说更多更明显的灰度特征),这将有利于DIC方法子区的准确识别,尤其适合于大变形或“退相关”明显的情况。另一方面,δf越大,对散斑图局部而言表示灰度的对比度越强烈,或者说相邻像素间的灰度级差越大。
尽管平均灰度梯度在散斑图质量评价中具有一定的有效性,但作者研究发现,具有相同平均灰度梯度的散斑图依然表现出完全不同的测量精度,在平均灰度梯度相同的情况下,测量误差与平均灰度2阶导数(用ωf表示)呈现出一定的规律,因此本文中提出平均灰度2阶导数这一新的散斑图质量评价参量结合平均灰度梯度对散斑图进行综合评价,其表达式为:
$ \omega_{\mathrm{f}}=\frac{\sum\limits_{i=1}^{W} \sum\limits_{j=1}^{H}\left|\nabla^{2} f\left(x_{i j}\right)\right|}{W \times H} $
(2) 式中, $ \left|\nabla^{2} f\left(x_{i j}\right)\right|=\sqrt{f_{x x}\left(x_{i j}\right)^{2}+f_{y y}\left(x_{i j}\right)^{2}} $是每个像素点灰度2阶导数矢量的模(因此图像灰度重建是在x和y两个方向进行插值,所以这里不考虑交叉项fxy), fxx(xij),fyy(xij)为像素点xij处在x和y两个方向的灰度2阶导数,可利用如下2阶差分算子进行计算:
$ \left\{\begin{array}{l} f_{x x}\left(x_{i j}\right)=f(i, j-1)-2 f(i, j)+f(i, j+1) \\ f_{y y}\left(x_{i j}\right)=f(i-1, j)-2 f(i, j)+f(i+1, j) \end{array}\right. $
(3) -
DIC方法的位移测量误差来自两个方面:系统误差和随机误差。系统误差一般是指由亚像素插值方法所导致的位移测量误差;随机误差是指由图像采集设备(如CCD, CMOS等)暗电流引起的图像噪声所导致的位移测量误差。DIC方法为了得到亚像素测量精度,在利用N-R等迭代算法使互相关系数达到极值过程中,图像亚像素位置的灰度及灰度导数信息需通过具体插值来获取,而通常所采用的插值算法均存在一定的相位误差,使得DIC方法在利用具体插值算法获取图像亚像素位置的灰度及灰度导数过程中不可避免地带入了系统误差(插值误差),参考文献[14]中给出了三次Lagrange插值算法的系统误差表达式:
$ \begin{array}{c} e_\text{s}=\frac{1}{\pi k} \cdot \\ \arctan \left[\frac{\left(\frac{9}{4} \delta-\delta^{3}\right) \sin \left(\frac{\pi k}{2}\right)-\left(\frac{\delta}{12}-\frac{\delta^{3}}{3}\right) \sin \left(\frac{3 \pi k}{2}\right)}{\left(-\frac{\delta^{2}}{2}+\frac{9}{8}\right) \cos \left(\frac{\pi k}{2}\right)+\left(\frac{\delta^{2}}{2}-\frac{1}{8}\right) \cos \left(\frac{3 \pi k}{2}\right)}\right]- \\ \delta \end{array} $
(4) 式中, es为系统误差,k为归一化波数(周期为T的正弦波,归一化波数与周期T之间的关系为k=2/T),δ为亚像素位移。由(4)式可知,系统误差与图像信号频率和亚像素位移值有直接关系,图像的信号频率越高系统误差也越大,系统误差在亚像素位置上呈正弦函数形式分布。
本文中的研究结果显示,散斑图质量的好坏在一定程度上跟散斑图具有的平均灰度梯度有关系,但并非取决于平均灰度梯度,具有相同平均灰度梯度的散斑图可以表现出完全不一样的测量精度。平均灰度梯度在一定程度上只反映了散斑图所包含的信息量或特征量,而无法体现特征信息的灰度分布形式,这就需要其它新的参量来表征散斑图的灰度分布形式。
图 1a和图 1b分别为两个灰度子区(或特征子区),其大小均为9pixel×9pixel。图 1a中有17个灰度级(8bit图),灰度分布按一定规律排列,其中任意位置灰度值与其相邻位置的灰度值相差均为15,并且在两个方向上呈递减或递增趋势。图 1b与图 1a具有相同的灰度信息(即具有相同数量的灰度级,且每一个灰度级对应相同数量的像素个数),但每一像素位置的灰度信息呈随机分布。表 1中给出了通过计算得到的图 1a、图 1b两个灰度子区的平均灰度梯度和平均灰度2阶导数。从图 1b可以看出,由于相邻像素之间的灰度级差较大且灰度波动剧烈,使得图 1b图具有很高的平均灰度梯度和平均灰度2阶导数,因此,灰度2阶导数反映了灰度梯度的变化程度。图 1a中,由于灰度分布按一定规律排列,相邻像素间具有一定灰度梯度而灰度梯度的变化保持不变,使图 1a具有一定的平均灰度梯度和为零的平均灰度2阶导数,因此, 平均灰度2阶导数在一定程度上反映了散斑图的灰度分布形式。
Table 1. MIG and MISD of two image subsets produced by computer simulation
由(4)式可知,为了降低系统误差,应使用频率较低的图像,频率较低的图像可以带来较小的插值误差。本文中图像的信号频率、平均灰度梯度、平均灰度1阶导数虽属于3个不同的概念,但它们之间又存在着一定的联系。一般而言,图像信号频率高意味着相邻像素间的灰度梯度大,图像灰度波动剧烈,导致高的平均灰度2阶导数;图像信号频率低意味着相邻像素间的灰度梯度小,图像灰度波动平缓,导致低的平均灰度2阶导数。DIC方法通过唯一识别特征子区来进行位移测量,因此特征子区必须具有一定的灰度梯度,因此, 可以利用具有一定灰度梯度而灰度波动(或灰度梯度变化)平缓的图像作为散斑图,而平均灰度2阶导数可以很好地量化图像灰度波动(或灰度梯度变化)的情况。
-
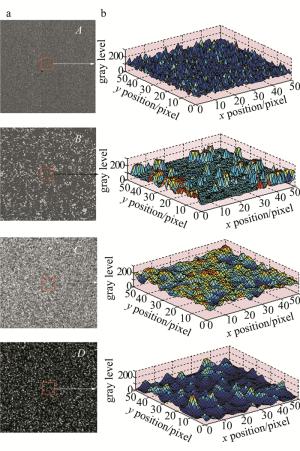
验证实验分两组进行,两组实验中分别选取了4幅散斑图进行亚像素平移实验。第1组实验中,为了研究散斑图平均灰度2阶导数对DIC方法位移测量精度的影响,因此选取了4幅几乎具有相同平均灰度梯度的散斑图,其分辨率均为401pixel×401pixel,这4幅散斑图的灰度分布及局部灰度3维分布如图 2所示。其中,散斑图A, B, C是实际实验中通过CCD拍摄得到,散斑图D为计算机仿真图,具体数学表达式[19]如下:
$I(\boldsymbol{r})=\sum\limits_{k=1}^{S} I_{0} \exp \left(-\frac{\left|\boldsymbol{r}-\boldsymbol{r}_{k}\right|}{R^{2}}\right) $
(5) 式中,S是散斑颗粒的总数目,I0是散斑颗粒中心的随机分布光强,r表示图像坐标位置,rk=(xk, yk)T是随机分布散斑颗粒中心的位置坐标,R是随机分布散斑颗粒的大小。
实验过程中,利用傅里叶变换对图 2所示的4幅散斑图施加位移精确可控的平移。每一幅图像连续平移20次,最大位移平移量为1pixel,相邻两幅散斑图之间的平移量为0.05pixel,将连续平移20次的图像序列作为变形后图像,然后利用N-R方法对参考图像(未变形图像)中3721(61×61)个均匀分布点的亚像素位移进行计算,计算子区大小均为41pixel×41pixel。图 3所示为计算得到的各散斑图对应亚像素位移下的位移均值误差和标准差。从计算结果可以看出,虽然4幅散斑图具有几乎相同的平均灰度梯度,但计算结果中无论位移均值误差还是标准差各不相同且差异较大,因此, 不能仅从平均灰度梯度这一统计量来对散斑图质量进行有效评价。从表 2和图 3可以明显看出,对于4幅不同的散斑图,位移计算均值误差和标准差也不同,具有较小平均灰度2阶导数散斑图的计算均值误差和标准差也较小。散斑图平均灰度2阶导数与图像灰度梯度变化程度(或图像灰度波动剧烈程度)有关系,灰度波动越剧烈其平均灰度2阶导数也越高。图像灰度波动程度反映出图像中信号频率的高低,而图像中信号频率的高低又导致图像插值误差的大小,因此,平均灰度2阶导数这一概念可以反映DIC方法的系统误差。
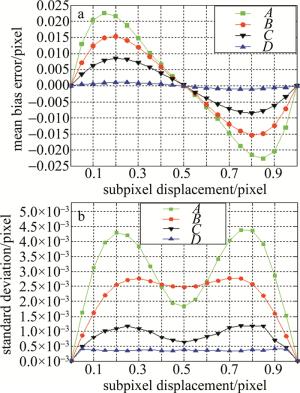
Figure 3. Mean bias errors and standard deviation of subpixel displacement for speckle patterns A, B, C, D
Table 2. MISD and MIG of speckle patterns A, B, C, D
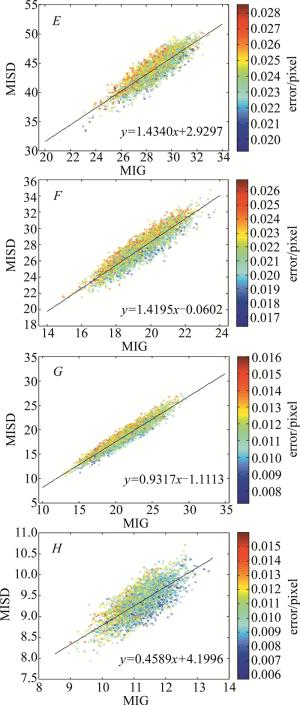
speckle pattern A B C D MIG 20.11 20.87 20.29 20.30 MISD 62.00 47.42 29.37 17.78 为了进一步研究平均灰度2阶导数在散斑图质量评价中的有效性,进行了第2组实验。第2组实验中综合考虑了平均灰度梯度和平均灰度2阶导数的情况。选取4幅(E, F, G, H)散斑颗粒大小基本接近、散斑颗粒分布均匀且平均灰度梯度和平均灰度2阶导数各异(如表 3所示)的散斑图,4幅散斑图分辨率均为701pixel×701pixel。实验中同样对4幅散斑图进行亚像素平移,平移量为0.2pixel(因为图 3中在0.2pixel左右位置测量均值误差最大,所以本实验中取该位置)。对每幅散斑图中均匀分布的3721(61×61)个点的位移进行计算,计算子区大小为21pixel×21pixel,同时计算图像子区的平均灰度2阶导数及平均灰度梯度,并采用双三次和双三次B样条两种插值方法。
Table 3. MISD and MIG of speckle patterns E, F, G, H
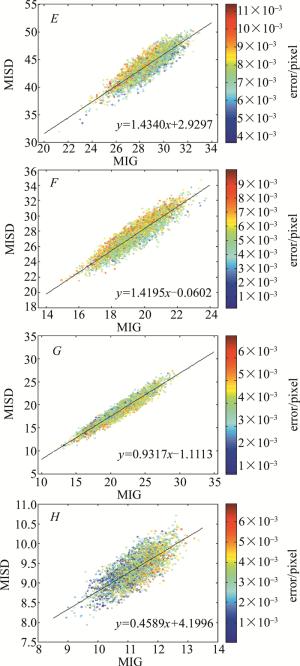
speckle pattern E F G H MIG 28.38 19.05 21.04 11.16 MISD 44.09 27.26 18.57 9.33 图 4中给出了4幅散斑图及其中心区域(51pixel×51pixel)局部放大图及对应y方向的fy和fyy分布图。图 5、图 6所示为4幅散斑图各计算点对应计算子区的平均灰度梯度、平均灰度2阶导数及位移计算误差散点分布图。从图 5、图 6计算结果可以得出如下结论:散斑图的平均灰度梯度和平均灰度2阶导数具有一定相关性,具有较高平均灰度梯度的图像子区,其平均灰度2阶导数也较高。对于某一固定的平均灰度梯度,从图 5、图 6可以看出,位移计算误差较大的计算点基本分别在左上侧,说明图像子区的平均灰度2阶导数越大位移计算误差也越大;其次,本文中通过对离散点进行线性回归,得到了各散斑图计算均值误差与回归系数之间的关系(见图 7),结果显示:回归系数越小,位移测量均值误差越小;回归系数越大,位移测量均值误差也越大;而且本文中所采用的两种插值方法表现出基本相同的上述规律,只是不同的插值方法对应不同的计算误差。
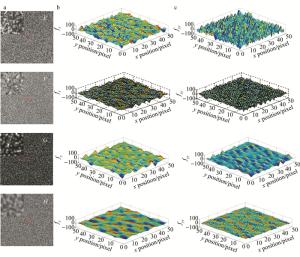
Figure 4. Speckle patterns E, F, G, H and distribution diagram of fy and fyy in the corresponding rectangular regions
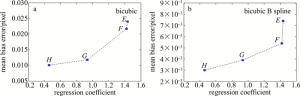
Figure 7. Relationship between mean bias error and regression coefficient of speckle pattern E, F, G, H
上述实验表明,平均灰度梯度和平均灰度2阶导数均与位移测量误差有关系,其原因在于平均灰度梯度反映了散斑图所包含灰度信息的量及灰度信息的明显程度,子区灰度信息量越大特征越明显,越有利于子区被唯一识别;平均灰度2阶导数反映了散斑图所包含灰度信息的分布形式(灰度波动情况),一般而言,对于具有一定平均灰度梯度的散斑图,其灰度曲面越光滑,平均灰度2阶导数越小,位移测量误差也越小。因此,实际实验中高质量散斑图的制备与选取应该使散斑图具有明显的特征信息(高的平均灰度梯度)、平缓的灰度过渡或灰度波动(低的平均灰度2阶导数)。同一散斑图其平均灰度梯度和平均灰度2阶导数对散斑图质量的影响看似矛盾,其实高质量散斑图是平均灰度梯度和平均灰度2阶导数的某一平衡。
-
散斑图作为物体表面变形信息的载体,其质量对数字图像相关方法位移测量精度有着十分重要的影响,本文中基于数字图像相关方法位移测量精度基本理论,分析了位移测量误差与图像灰度信息分布之间的关系,提出平均灰度2阶导数这一概念对实际散斑图质量进行评价。利用相关实验进行验证,实验结果显示, 位移测量精度不仅与散斑图具有的平均灰度梯度有关,而且与平均灰度2阶导数有着直接关系,对于具有相同平均灰度梯度的散斑图,其平均灰度2阶导数越小,位移测量误差也越小。因此,在实际应用中,散斑图质量的评价应综合考虑平均灰度2阶导数和平均灰度梯度两个参量对散斑图质量的影响。另外,在实际应用中还应考虑实验环境(噪声、高温等)、图像采集设备分辨率、物体变形大小等因素对散斑图进行合理的选取。
数字图像相关法散斑图质量评价方法
Assessment method of speckle pattern quality in digital image correlation
-
摘要: 为了研究数字图像相关方法中散斑图质量的有效评价问题, 采用散斑图质量表征参量——平均灰度2阶导数对散斑图质量进行了有效评价。通过分析图像插值误差与图像灰度信息分布形式之间关系, 指出散斑图平均灰度2阶导数与散斑图灰度信息分布形式之间的关系; 为了验证该散斑图质量表征参量的有效性, 利用傅里叶变换对散斑图进行平移实验, 通过Newton-Raphson(N-R)方法对平移前后的散斑图进行亚像素位移计算, 由位移计算结果可知, 具有低的平均灰度2阶导数的散斑图对应小的位移测量误差。结果表明, 平均灰度2阶导数在散斑图质量评价中具有一定的有效性; 在实际应用中, 应结合散斑图平均灰度2阶导数和平均灰度梯度对散斑图质量进行综合有效的评价。该研究为高质量散斑图的制备与选取提供了参考。Abstract: In order to study the effective evaluation of speckle image quality in digital image correlation method, the quality of speckle pattern was effectively evaluated by means of the second derivative of average gray level of quality characterization parameter of speckle pattern. By analyzing the relationship between image interpolation error and the distribution of image gray information, the relationship between the second derivative of average gray level of speckle pattern and the distribution form of gray level information of speckle pattern was pointed out. In order to verify the validity of the quality characterization parameters of the speckle pattern, Fourier transform was used to translate the speckle pattern. The sub-pixel displacement of speckle pattern before and after translation was calculated by Newton-Raphson method. According to the displacement calculation results, speckle pattern with low average gray second derivative corresponded to small displacement measurement error. The results show that, the second derivative of average gray level is effective in the quality evaluation of speckle pattern. In practical application, the quality of speckle pattern should be evaluated comprehensively and effectively by combining the second derivative of average gray level and average gray gradient of speckle pattern. This study provides a reference for the preparation and selection of high quality speckle patterns.
-
Table 1. MIG and MISD of two image subsets produced by computer simulation
Table 2. MISD and MIG of speckle patterns A, B, C, D
speckle pattern A B C D MIG 20.11 20.87 20.29 20.30 MISD 62.00 47.42 29.37 17.78 Table 3. MISD and MIG of speckle patterns E, F, G, H
speckle pattern E F G H MIG 28.38 19.05 21.04 11.16 MISD 44.09 27.26 18.57 9.33 -
[1] BRUCK H A, MCNEIL S R, SUTTON M A, et al. Digital image co-rrelation using Newton-Raphson method of partial differential correction[J]. Experimental Mechanics, 1989, 29(3):261-267. doi: 10.1007/BF02321405 [2] LIU Y, XIAO Sh D, ZHANG R, et al. Initial estimation of digital image correlated deformation based on genetic algorithms [J].Laser Technology, 2020, 44(1): 130-135 (in Chinese). [3] ZHANG H J, LI G H, LIU Ch, et al. Reliable initial guess based on SURF feature matching in digital image correlation[J]. Acta Optica Sinsca, 2013, 33(11):1112005(in Chinese). doi: 10.3788/AOS201333.1112005 [4] XIE J Y, XU Y J, WANG X G. Vision measurement method based on Bayesian model and digital image correlation [J]. Laser Technology, 2016, 40(6): 866-870(in Chinese). [5] PETERS W H, RANSON W F. Digital imaging techniques in experimental stress analysis[J]. Optical Engineering, 1982, 21(3):427-432. [6] RONG W X, QIAN X F, LIU B, et al. Algorithm of in-plane displacement measured by speckle photography based on phase of Fourier transform[J]. Laser Technology, 2017, 41(4):473-478(in Chin-ese). [7] LIANG Zh J, WANG K F, GU G Q, et al. Digital speckle image correlation method base on particle swarm optimization algorithm[J]. Laser Technology, 2014, 38(5): 603-607(in Chinese). [8] DONG Sh, DAI Y T, DONG E L, et al. Three-dimensional reconstruction of dental impression based on multi-camera three-dimensional digital image correlation method[J]. Acta Optica Sinsca, 2015, 35(8):0812006(in Chinese). doi: 10.3788/AOS201535.0812006 [9] LECOMPTE D, SMITS A, BOSSUYT S, et al. Quality assessment of speckle patterns for digital image correlation[J]. Optics and Lasers in Engineering, 2006, 44(11):1132-1145. doi: 10.1016/j.optlaseng.2005.10.004 [10] ZHAO J Q, ZENG P, LEI L P, et al. Initial guess by improved population-based intelligent algorithms for large inter-frame deformation measurement using digital image correlation[J]. Optics and Lasers in Engineering, 2012, 50(3):473-490. doi: 10.1016/j.optlaseng.2011.10.005 [11] CRAMMOND G, BOYD S W, DULIEU-BARTON J M. Speckle pattern quality assessment for digital image correlation[J]. Optics and Lasers in Engineering, 2013, 51(12):1368-1378. doi: 10.1016/j.optlaseng.2013.03.014 [12] WANG Y Q, SUTTON M A, BRUCK H A, et al. Quantitative error assessment in pattern matching: Effects of intensity pattern noise, interpolation, strain and image contrast on motion measurements[J]. Strain, 2009, 45(2):160-178. doi: 10.1111/j.1475-1305.2008.00592.x [13] VENDROUX G, KNAUSS W G. Submicron deformation field mea-surements(Ⅱ): Improved digital image correlation[J]. Experimental Mechanics, 1998, 38(2):86-92. doi: 10.1007/BF02321649 [14] SCHREIER H W, BRAASCH J R, SUTTON M A. Systematic errors in digital image correlation caused by intensity interpolation[J]. Optical Engineering, 2000, 9(11):2915-2921. [15] SCHREIER H W, SUTTON M A. Systematic errors in digital image correlation due undermatched subset shape functions [J]. Experimental Mechanics, 2002, 42(3):303-310. doi: 10.1007/BF02410987 [16] PAN B, XIE H M, XU B Q, et al. Performance of sub-pixel registration algorithms in digital image correlation[J]. Measurement Science & Technology, 2006, 17(6):1615-1621. [17] WANG Zh Y, WANG L, GUO W, et al. Optimal size of speckle spot in digital image correlation method[J]. Journal of Tianjin University, 2010, 43(8):674-678(in Chinese). [18] SATURU Y, HISAO K. Lens distortion correction for digital image correlation by measuring rigid body displacement [J]. Optical Engineering, 2006, 45(2):023602. doi: 10.1117/1.2168411 [19] ZHOU P, GOODSON K E. Sub-pixel displacement and deformation gradient measurement using digital image/speckle correlation (DISC) [J]. Optical Engineering, 2001, 40(8):1613-1620. doi: 10.1117/1.1387992 [20] PAN B, LU Z X, XIE H M. Mean intensity gradient: An effective global parameter for quality assessment of the speckle patterns used in digital image correlation [J]. Optics and Lasers in Engineering, 2010, 48(4):469-477. doi: 10.1016/j.optlaseng.2009.08.010 -


 网站地图
网站地图


 下载:
下载: