-
跳动误差指被测实体表面绕基准轴线连续回转时所允许的最大跳动量。在生产加工中,轴类零件的径向跳动会引起机器振动、噪声增大等影响[1]。目前国内对主轴径向跳动测量方法大多使用千分尺或者是三坐标测量机等,人工操作不仅效率低而且误差较大,而三坐标测量机尺寸较大,使用成本高[2]。随着当前传感器技术,尤其是光电类传感器的发展,轴类零件的径向跳动测量开始由原先的接触式测量逐步转变为智能化的非接触式测量[3]。目前的非接触检测法有激光位移传感器测量和基于机器视觉的CCD面阵测量法等[4-5]。本文中提出一种基于激光测量的全光纤光路测量方法,利用声光效应布喇格衍射产生两级测量光形成光外差检测法,具有抗干扰能力强、稳定性好的优点,理论上有较高的测量精度。
-
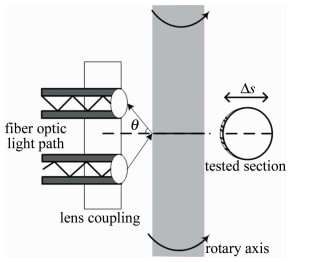
测量示意图如图 1所示。激光通过光纤透镜耦合的测量探头照射在被测轴的表面,组成了反射式光纤位移传感器的形式[6]。转动轴在工作状态下的径向跳动会在光路的2维平面内形成位移差Δs,其速度变化表示为vs,由于测量距离的变化,入射光和反射光发生多普勒频移现象[7],vs通过光路的频移转化为混频器中的电信号,再经过电信号的处理即可换算为轴的径向跳动量。
-
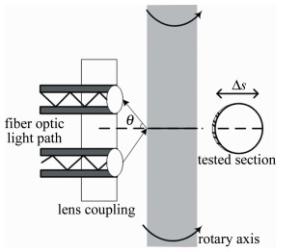
为解决测量前激光测量光路需要大量调试的问题,在全部测量光路上使用光纤进行光路的传导,在测量装置前端的光路准直性较好,所以激光器和光纤的耦合采用直接耦合的方式,布喇格盒与光纤选择透镜耦合的方式[8-10],将0级光和-1级光分别耦合到两个光纤光路,示意图如图 2所示。
选择Coning公司的SMF-28型光纤,纤芯半径a=4.07μm;纤芯折射率n1=1.45205;包层折射率n2=1.44681。选择的He-Ne激光器波长λ=632.8nm。根据光纤的导光原理[11],光纤的截止波长λc=2πan1×$\sqrt {2\Delta } $/2.405,其中Δ=(n1-n2)/n1,代入可得λ>λc,因此光路在此光纤中为单模传输,不存在模式色散现象,光路传输可靠。
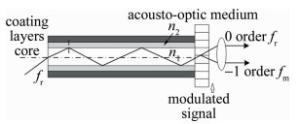
激光器产生的激光频率为fr的激光束,直接耦合到光纤,经全反射后再进入布喇格盒,调整布喇格晶体角度产生只有0级光fr和-1级光fm的布喇格衍射,再经过透镜耦合的方式分别进入两路单模光纤[12-13],示意图如图 3所示。此种设计降低了空气光路中的外界光干扰。耦合装置与布喇格盒相对固定,只需调整晶体的角度改变入射角即可得到布喇格衍射[14],降低了调试难度,提高了测量效率。
-
采用SO2000型声光器件,大量的声光实验表明, 采用100MHz的调制频频率可以得到输出较为稳定的布喇格衍射[15],所以本系统的调制频率fb=100MHz。
总体测量原理如图 4所示。为实现同一轴线上的差动测量,0级光fr经分光器后分为fr, 1和fr, 2两束光作为参考光;布喇格衍射后-1级光fm经分光器后分为fm, 1和fm, 2两束光作为测量光,其通用表达为fm=fr-fb,fb为声光调制频率;测量光经过光纤透镜耦合射出,在被测面经散射后得到两束散射光fm, 1′和fm, 2′,其通用表达为fm′=fm±fD,fD为转轴上的多普勒频移[16]。
根据激光多普勒测速原理可得:
$ {f_{\rm{D}}} = 2{v_{\rm{s}}}\cos \theta /\lambda $
(1) 式中, θ为反射光线和物体垂直方向的夹角。两路散射光经光纤透镜采集后分别进入两个光电探测器和参考光混频[17-18]:根据混频原理,可以响应的频率Δf为参考光的频率和散射光频率之差,即:
$ \begin{array}{*{20}{c}} {\Delta f = {f_{\rm{r}}} - f_{\rm{m}}^\prime = {f_{\rm{r}}} - {f_{\rm{m}}} \pm {f_{\rm{D}}} = }\\ {{f_{\rm{r}}} - \left( {{f_{\rm{r}}} - {f_{\rm{b}}}} \right) \pm {f_{\rm{D}}} = {f_{\rm{b}}} \pm {f_{\rm{D}}}} \end{array} $
(2) 式中,fb-fD和fb+fD分别为两路差分频移。
具体的混频推导为:参考光fr和反射测量光fm′照射到以雪崩二极管为核心的探测器上,两路光的初相位分别为φ1和φ2,其合成电场强度为:
$ E = {E_1}\cos \left( {2{\rm{ \mathsf{ π} }}{f_{\rm{r}}}t + {\varphi _1}} \right) + {E_2}\cos \left( {2{\rm{ \mathsf{ π} }}f_{\rm{m}}^\prime t + {\varphi _2}} \right) $
(3) 由于雪崩二极管的非线性特性,场强的混频展开式E(t)为:
$ \begin{array}{*{20}{c}} {E(t) = {k_0} + {k_1}E + {k_2}{E^2} = }\\ {{k_0} + {k_1}{E_1}\cos \left( {2{\rm{ \mathsf{ π} }}{f_{\rm{r}}}t + {\varphi _1}} \right) + {k_1}{E_2}\cos \left( {2{\rm{ \mathsf{ π} }}f_{\rm{m}}^\prime t + {\varphi _2}} \right) + }\\ {{k_2}E_1^2{{\cos }^2}\left( {2{\rm{ \mathsf{ π} }}{f_{\rm{r}}}t + {\varphi _1}} \right) + {k_2}E_2^2{{\cos }^2}\left( {2{\rm{ \mathsf{ π} }}f_{\rm{m}}^\prime t + {\varphi _2}} \right) + }\\ {{k_2}{E_1}{E_2}\cos \left[ {2{\rm{ \mathsf{ π} }}\left( {{f_{\rm{r}}} + f_{\rm{m}}^\prime } \right)t + \left( {{\varphi _1} + {\varphi _2}} \right)} \right] + }\\ {{k_2}{E_1}{E_2}\cos \left[ {2{\rm{ \mathsf{ π} }}\left( {{f_{\rm{r}}} - f_{\rm{m}}^\prime } \right)t + \left( {{\varphi _1} - {\varphi _2}} \right)} \right]} \end{array} $
(4) 式中, k0, k1, k2是与光电探测器有关的常数。激光器的频率数量级为1014,光电探测器无法响应这样的高频,因此频率成分为fr,fm′和fr+fm′的均无法响应,再使用电容隔去直流分量,因此探测器输出E1(t)仅为:
$ {E_1}(t) = {k_2}{E_1}{E_2}\cos \left[ {2{\rm{ \mathsf{ π} }}\left( {{f_{\rm{r}}} - f_{\rm{m}}^\prime } \right)t + \left( {{\varphi _1} - {\varphi _2}} \right)} \right] $
(5) 可以看出, 上式就是(2)式所表示的Δf的交变信号。将上式简写为:
$ {E_1}(t) = {A_1}\cos (2{\rm{ \mathsf{ π} }}\Delta ft + \Delta \varphi ) $
(6) 由(2)式可知,Δf为调制信号和多普勒频移的和差项,用相敏检波器将多普勒频移从调制信号Eb(t)=Abcos(2πfb+φb)中选出,其中Ab为调制信号幅值,φb为调制信号相位,即:
$ \begin{array}{*{20}{c}} {{E_0}(t) = {E_1}(t){E_{\rm{b}}}(t) = {A_1}\cos (2{\rm{ \mathsf{ π} }}\Delta ft + \Delta \varphi ) \cdot }\\ {{A_{\rm{b}}}\cos \left( {2{\rm{ \mathsf{ π} }}{f_{\rm{b}}} + {\varphi _{\rm{b}}}} \right) = }\\ {\frac{1}{2}{A_1}{A_{\rm{b}}}\cos \left[ {2{\rm{ \mathsf{ π} }}\left( {2{f_{\rm{b}}} + {f_{\rm{D}}}} \right)t + \Delta \varphi + {\varphi _{\rm{b}}}} \right] + }\\ {\frac{1}{2}{A_1}{A_{\rm{b}}}\cos \left( {2{\rm{ \mathsf{ π} }}{f_{\rm{D}}}t + \Delta \varphi - {\varphi _{\rm{b}}}} \right)} \end{array} $
(7) 使用低通滤波器滤除高频项,最终的多普勒频移项ED(t)为:
$ {E_{\rm{D}}}(t) = {A_{\rm{D}}}\cos \left( {2{\rm{ \mathsf{ π} }}{f_{\rm{D}}}t + {\varphi _{\rm{D}}}} \right) $
(8) 式中, AD=A1Ab/2,φD=Δφ-φb。将(8)式经频率/电压转换可得电压为:U(t)=K·fD, 其中K转换系数。把fD代入(1)式可得:
$ {v_{\rm{s}}} = \frac{\lambda }{{2K\cos \theta }}U(t) $
(9) 积分得径向跳动量:
$ \Delta s = \frac{\lambda }{{2K\cos \theta }}\int_0^t U (t){\rm{d}}t $
(10) 由上式,对频压转换的电压值取积分运算即可得到一路位移量。两路差动信号的最终径向跳动量Δx=(Δs1+Δs2)/2;在同一轴线上的两路数据取其平均值Δx即为径向跳动值。
-
径向跳动的现场测量是检测垂直于轴径方向上的位移峰峰值Δs。为了检验系统的测量精度,选取特鲁斯T-20跳动测量仪和设计的测量系统进行对比实验。为了先验证全光纤测量光路声光调制理论本身的测量精度,使用单测量头对一主轴多个截面进行测量,结果如表 1所示。
Table 1. Comparison of single measurement head
1 2 3 4 5 6 7 Δs of T-20/μm 1.486 1.453 1.398 1.427 1.378 1.436 1.441 Δs of system/
μm1.4725 1.4654 1.4013 1.4179 1.3759 1.4248 1.4486 T-20跳动仪测量数据的平均值x1=1.4313μm,系统测量数据的平均值为x2=1.4295μm,则相对误差为:
$ e = \frac{{\left| {\overline {{x_2}} - \overline {{x_1}} } \right|}}{{\overline {{x_1}} }} \times 100\% = 0.1258\% $
(11) 上述实验中得出使用单测量头对7个截面分别测量,平均跳动误差为1.4295μm,和跳动测量仪的相对误差为0.1258%。
因为使用全光纤光路的优越性,在现场实验可以容易做到同一轴线上的差分测量,这是传统空气光路难以做到的。在理论上是可以消除测量系统的共模干扰。使用双测量头差分测量结果如表 2所示。
Table 2. Comparison of dual-probe differential measurement results
1 2 3 4 5 6 7 Δs of T-20/μm 1.475 1.443 1.386 1.413 1.392 1.449 1.467 Δs of system
1/μm1.4615 1.4547 1.3923 1.3986 1.3789 1.4238 1.4546 Δs of system
2/μm1.4793 1.4362 1.3786 1.4227 1.4125 1.4675 1.4728 Δx/μm 1.4704 1.4454 1.3854 1.4106 1.3957 1.4457 1.4637 使用双探头差分测量的径向跳动平均跳动量Δx=1.4309μm,相对误差为0.0838%,相对误差减小了0.042%。上述数据表明,双探头差分测量的方法可以显著提高测量精度,使测量的相对误差小于0.1%,达到了系统设计的要求。
-
本系统中采用632.8nm波长的He-Ne激光器,光纤中声光调制的光波稳定性小于0.05%,用矩形分布估计其不确度为3.45×10-4。
-
在进行数据处理时假定在耦合透镜处的入射光线和反射光线与传感器振动方向的夹角不变。实际上由于距离原因,该夹角在(θ-Δθ)~(θ+Δθ)之间变化,最大误差限为0.06%,用三角分布可估算其不确定度为2.45×10-4。
-
本系统中选择的雪崩二极管光电探测器的波长范围为600nm~1200nm,扩展不确定度为0.09%,置信概率p=99%,包含因子k=2.576,所以可得由光电探测器导致的标准不确定度为3.12×10-4。
-
使用全光纤光路和声光调制使系统信噪比得到有效的改善,经实验验证这一部分产生的误差实验测量得电路产生的误差不高于0.05%,用正态分布估计其不确定度为1.67×10-4。
-
由于系统受到外界温度、湿度、振动噪声等干扰,实验结果表明, 这部分误差总体小于0.08%,用正态分布估计其不确定度为2.67×10-4。
因此,合成标准不确定度为:
$ \begin{array}{*{20}{c}} {{u_{\rm{c}}} = \sqrt {u{{\left( \lambda \right)}^2} + u{{(\theta )}^2} + u{{(d)}^2} + u{{(i)}^2} + u{{(o)}^2}} = }\\ {0.06129\% < 0.1\% } \end{array} $
(12) 由此可得系统的不确定度小于0.1%,达到设计要求。
-
在对径向跳动测量进行了一系列的理论推导后,设计了测量系统并进行了实验。实验的横向对比和纵向对比均表明,系统可以进行实用高效的径向跳动检测。相较于其它激光类测量装置,全光纤光路的使用大大提高了光路传输效率,提高了测量精度;光外差法测量原理的灵活运用也使系统达到了纳米级的测量精度;利用光纤的几何形状易于调整的特性,在光路测量终端提出同一轴线上的差分测量方法,抑制了系统本身的共模干扰,进一步地提高了测量信噪比。实验和不确定度评定表明, 系统可以进行高精度、非接触式的纳米级径向跳动测量,在生产加工现场的应用有广阔的前景。
全光纤声光调制径向跳动差分测量技术研究
Research of radial run-out differential measurement technology with all fiber acousto-optic modulation
-
摘要: 为了实现机床在加工状态下主轴径向跳动非接触、高精度的测量,采用光外差法光路的激光多普勒差分检测方法,进行了理论分析和实验验证。直接耦合和透镜耦合的全光纤光路的应用,降低了布喇格衍射光路的调节难度,提高了测量分辨率和抗干扰能力,减小了噪声;光纤分光器实现了同一轴线上的差分测量,抑制了因测量光路本身的振动带来的干扰。得到了相对误差为0.0838%的主轴径向跳动测量结果,实现了纳米级跳动误差测量。结果表明,系统的相对误差和测量不确定度均小于0.1%。该研究对主轴径向跳动的实时测量有一定的指导意义。Abstract: In order to realize non-contact and high-precision measurement of the radial run-out of the spindle in the machining state, the laser Doppler differential detection method based on the optical heterodyne method was used for theoretical analysis and experimental verification. The application of direct coupling and lens-coupling all-fiber optical path reduces the adjustment difficulty of the Bragg diffraction optical path, improves the measurement resolution and anti-interference ability, and reduces the noise; the optical fiber splitter realizes the differential measurement on the same axis, suppressing interference caused by the vibration of the measuring optical path itself. The radial run-out measurement result of the spindle with a relative error of 0.0838% is obtained, and the nanometer run-out error measurement is realized. The results show that the relative error and measurement uncertainty of the system are less than 0.1%. This study has a certain guiding significance for the real-time measurement of the radial run-out of the main shafts.
-
Table 1. Comparison of single measurement head
1 2 3 4 5 6 7 Δs of T-20/μm 1.486 1.453 1.398 1.427 1.378 1.436 1.441 Δs of system/
μm1.4725 1.4654 1.4013 1.4179 1.3759 1.4248 1.4486 Table 2. Comparison of dual-probe differential measurement results
1 2 3 4 5 6 7 Δs of T-20/μm 1.475 1.443 1.386 1.413 1.392 1.449 1.467 Δs of system
1/μm1.4615 1.4547 1.3923 1.3986 1.3789 1.4238 1.4546 Δs of system
2/μm1.4793 1.4362 1.3786 1.4227 1.4125 1.4675 1.4728 Δx/μm 1.4704 1.4454 1.3854 1.4106 1.3957 1.4457 1.4637 -
[1] ZHAO Y P. Design of pump rotor static deflection and radial run-out detection system[D]. Shenyang: Shenyang University of Technology, 2018: 2-19(in Chinese). [2] SI Zh Y, YU Y J, MA W, et al. Simulation analysis of radial run-out of cylindrical roller bearings[J]. Bearing, 2019, 470(1):23-27(in Chinese). [3] WANG Zh J, SHENG W T, XIE J Y, et al. Study on the positioning measurement of cylindrical objects based on linear laser triangulation[J/OL].(2018-09-30)[2019-03-18].http://kns.cnki.net/kcms/detail/51.1125.TN.20180930.1150.010.html(in Chinese). [4] LIU X B, TANG J, LI M Q. Non-same frequency component of laser measurement radial run-out under turning conditions[J]. Machine Tool & Hydraulics, 2018, 46(22): 116-119(in Chinese). [5] YU P, SHAN D R. Study on three-point measurement of radial round jump error of shaft parts[J].Machine Tool & Hydraulics, 2018, 46(7):35-37(in Chinese). [6] LI M H, CHENG L, LI Y M, et al. Design of U-wound fiber bending loss displacement sensor[J]. Journal of Optics, 2018, 38(6):94-101(in Chinese). [7] XING B, YU Z J, XU X N, et al. Defect monitoring based on laser doppler shift[J].China Optics, 2018, 11(6):991-1000(in Chin-ese). doi: 10.3788/co.20181106.0991 [8] JIANG S C. Development and optimization of fiber Bragg grating monitoring system and its application in slope engineering [D].Ji'nan: Shandong University, 2016: 54-68(in Chinese). [9] ZHOU M W, REN S Y, ZHU Y Q, et al. Study on the fusion cone type broadband fiber coupler[J/OL]. (2019-03-07)[2019-03-18].http://kns.cnki.net/kcms/detail/51.1125.TN.20190307.1126.006.html (in Chinese). [10] WANG Ch, FAN X B, TONG Sh F, et al. Coupling efficiency and influencing factors of spatial light to less mode fiber[J]. Acta Photonica Sinica, 2018, 47(12): 1206001 (in Chinese). doi: 10.3788/gzxb20184712.1206001 [11] LI J. Experimental study of non-tracking solar fiber light guiding system [D]. Nanning: Guangxi University, 2018: 25-34(in Chinese). [12] ZHU Zh J, XUE J W, WANG Y K, et al. 1064nm single-frequency fiber laser based on MOPA structure[J/OL]. (2019-03-07)[2019-03-18].http://kns.cnki.net/kcms/detail/51.1125.TN.20190307.1128.010.html (in Chinese). [13] ZHANG W D, LI X, BAI J H, et al. Light field generation and application of optical fiber structure[J/OL].(2018-10-07)[2019-03-13].http://kns.cnki.net/kcms/detail/31.1252.O4.2018.1007.1419.044.html (in Chinese). [14] WANG X Y, XU G K.A novel fiber coupling structure design for space communication[J].Laser Journal, 2019, 40(2):20-23(in Chinese). [15] DU Zh J. Research on fiber optic acousto-optic modulation vibration measurement technology [D]. Zibo: Shandong University of Technology, 2016: 7-18(in Chinese). [16] WANG H L, LIU Ch H. Research on laser roughness measurement technology based on acousto-optic modulation[J].Piezoelectrics & Acoustooptics, 2013, 35(6):797-800(in Chinese). [17] LIU B, CAO Ch D, YU X L, et al. Experimental experiment of laser coherent Doppler velocity measurement[J].Laser & Infrared, 2018, 48(12):1486-1490(in Chinese). [18] LIU K, WANG H L, SUN Sh Q. Study on electron modulation laser coherent shaft vibration measurement technology[J].Laser Technology, 2018, 42(4):466-469(in Chinese). [19] CAO M, WANG E, LI B, et al. Analysis of calibration and uncertainty of FBG displacement sensor[J]. Sensors and Microsystems, 2016, 35(4): 35-37(in Chinese). [20] LUO L M, LI A X, LIU J. Evaluation of uncertainty in measurement results of chassis dynamometer[J].China Metrology, 2019, 44(2):113-114(in Chinese). -


 网站地图
网站地图

 下载:
下载: