-
近年来,超短超强飞秒激光技术得到飞速发展,峰值功率由太瓦(TW,1012W)提高到几拍瓦(PW,1015W)甚至是数十拍瓦量级[1-2]。与此相应,激光脉冲的聚焦峰值功率密度也得到迅速提高,可达1020W·cm-2以上,远远大于相对论激光强度[3]。由于超强飞秒激光脉冲极高的峰值功率密度、电场强度、以及磁场强度等,它与物质相互作用时能够提供极端高温、高压等物理条件,使得超强飞秒激光脉冲在强场物理研究领域发挥了重要作用,甚至可以模拟天体物理中一些重要的过程。利用超短超强飞秒激光与固体靶或者气体靶相互作用,可以获得高品质的电子束、质子束、中子束等[4],可以研究极端高温、高压等物理条件下的材料特性。
在上面提到的超强飞秒激光脉冲与物质相互作用过程中,激光脉冲的聚焦特性对物理作用过程和作用结果起着非常重要甚至是决定性的影响,比如在激光尾波场电子加速中,聚焦光斑会影响电子束的稳定性、单能性、以及产额等[5-6]。因此在进行物理实验之前,必须对超强激光的聚焦特性进行精确测量,并给出相应的分析和评估[7-8]。原则上,在很多飞秒激光与物质相互作用的实验以及飞秒激光精密加工中,研究人员期望获得近衍射极限大小、高能量集中度的聚焦光斑,从而提高飞秒脉冲的聚焦峰值功率密度[9-11]。然而由于光学系统失调、光学镜片面形误差、以及镀膜缺陷等因素的影响,会给飞秒脉冲引入不利的相位畸变或者波前像差,如球差、慧差等,进而严重影响飞秒脉冲的聚焦特性。2011年,GONZÁLEZ-GALICIA等人基于赛德尔(Seidel)像差理论对超短飞秒激光脉冲通过消色差双透镜的聚焦特性进行了详细研究[12-13]。2015年,LI等人对高数值孔径下初级像差对高斯光束的聚焦特性进行了初步研究[14];同年,SUN等人对径向偏振飞秒脉冲的紧聚焦特性进行了数值模拟和实验研究[15-16]。然而这些研究均没有系统地给出不同波前像差情况下, 飞秒脉冲在聚焦焦平面处直观的2维强度场分布,以及光强分布随光束传输轴如何演化的过程。事实上,通过飞秒脉冲在焦平面处直观的2维强度场分布以及强度传输演化过程,一方面可以初步判断是否存在波前像差,另一面也能够为波前像差的补偿提供直接参考[17]。
本文中将基于瑞利-索末菲标量衍射理论,对比研究在各类波前像差下,包括场曲、像散、慧差、三叶形像差以及球差等,对具有均匀强度分布和高斯强度分布的超短飞秒激光脉冲聚焦特性的影响。该研究结果对超短飞秒激光束的光束质量评估及聚焦特性分析具有实际的指导意义。
-
Zernike多项式是定义在单位圆域上的正交多项式,因为它易与Seidel像差建立联系的特点,常被用作基底函数系对光束的波前像差进行拟合[18]。比如在激光系统中,利用Zernike多项式可以描述因腔镜失调、面形误差以及激光窗口热透镜效应等导致的波前畸变。Zernike多项式表示为[19]:
$ \left\{ \begin{array}{l} {Z_{{k_{\rm{e}}}}}(\rho ,\theta ) = \sqrt {2(n + 1)} {R_{n,m}}(\rho )\cos (m\theta ),(m > 0)\\ {Z_{{k_{\rm{o}}}}}(\rho ,\theta ) = - \sqrt {2(n + 1)} {R_{n,m}}(\rho )\sin (m\theta ),(m < 0)\\ {Z_k}(\rho ,\theta ) = \sqrt {n + 1} {R_{n,0}}(\rho ),(m = 0) \end{array} \right. $
(1) 式中,Z代表Zernike多项式,k为多项式阶数,下标ke代表k为偶数,下标ko代表k为奇数;n为径向自由度;m为角向频率,变化范围为-n, -n+2, …,n-2,n;ρ为单位圆上的半径,取值范围为[0, 1];极角θ的取值范围为[0,2π]。径向多项式Rn, m定义为:
$ \begin{array}{*{20}{c}} {{R_{n,m}}(\rho ) = }\\ {\sum\limits_{s = 0}^{\left( {n - \left| m \right|} \right)/2} {\frac{{{{( - 1)}^s}(n - s)!{\rho ^{n - 2s}}}}{{s!\left[ {\frac{{n + |m|}}{2} - s} \right]!\left[ {\frac{{n - |m|}}{2} - s} \right]!}}} } \end{array} $
(2) 基于Zernike多项式,则飞秒脉冲的波前像差φ(ω, r, θ)可以表示为[20]:
$ \varphi (\omega ,r,\theta ) = \sum\limits_{k = 1}^\infty {{c_k}} (\omega ){Z_k}(r/R,\theta ) $
(3) 式中,ω为激光角频率,r为径向坐标,ck为模式系数,R为激光光斑半径。由于飞秒脉冲的宽光谱特性,每个光谱元对应的模式系数可以表示为[20]:
$ {c_k}(\omega ) = {c_k}\left( {{\omega _0}} \right)\frac{\omega }{{{\omega _0}}} $
(4) 式中,ω0代表激光的中心频率。各阶Zernike多项式及对应的波前像差如表 1所示[19]。
Table 1. Zernike polynomial and the corresponding primary aberration
k n m Zk(ρ, θ) aberration 4 2 0 $\sqrt{3}$(2 ρ2-1) defocus 5 2 -2 $\sqrt{6}$ ρ2sin(2 θ) astigmatism 6 2 2 $\sqrt{6}$ ρ2cos(2 θ) astigmatism 7 3 -1 $\sqrt{8}$(3ρ2-2ρ)sin θ coma 8 3 1 $\sqrt{8}$(3ρ2-2ρ)cos θ coma 9 3 -3 $\sqrt{8}$ ρ3sin(3 θ) trefoil 10 3 3 $\sqrt{8}$ ρ3cos(3 θ) trefoil 11 4 0 $\sqrt{5}$ (6ρ4-6ρ2+1) spherical -
由于飞秒脉冲具有极高的峰值功率,因此对飞秒脉冲聚焦通常采用反射式的离轴抛物面镜进行。离轴抛物面镜无色散、色差,同时消除了光学非线性效应对超短脉冲激光的影响;而当入射光与光轴严格平行时,反射光可无球差的聚焦于焦点。离轴抛物面镜的面形误差以及调节精度对飞秒脉冲的聚焦特性具有重要影响[21],在本文中将离轴抛物面镜等效于理想的消色差透镜,从而可以利用瑞利-索末菲标量衍射理论重点讨论不同像差对飞秒脉冲聚焦特性的影响。
考虑两种情况:(1)入射飞秒脉冲具有均匀的强度分布;(2)入射脉冲具有高斯强度分布。这两种情况下的入射脉冲电场频域复振幅E可以分别表示为[21]:
$ \begin{array}{*{20}{c}} {E(\omega ,x,y,z = 0) = {E_0}\exp \left[ { - \frac{{{\tau ^2}{{\left( {\omega - {\omega _0}} \right)}^2}}}{4}} \right] \times }\\ {u(x,y)\exp [{\rm{i}}\varphi (\omega ,x,y,z = 0)]} \end{array} $
(5) $ \begin{array}{*{20}{c}} {E(\omega ,x,y,z = 0) = }\\ {{E_0}\exp \left[ { - \frac{{{\tau ^2}{{\left( {\omega - {\omega _0}} \right)}^2}}}{4}} \right]\exp \left( { - \frac{{{x^2} + {y^2}}}{{{R^2}}}} \right) \times }\\ {\exp [{\rm{i}}\varphi (\omega ,x,y,z = 0)]} \end{array} $
(6) 其中,
$ u(x,y) = \left\{ {\begin{array}{*{20}{l}} {1,\left( {\sqrt {{x^2} + {y^2}} \le R} \right)}\\ {0,\left( {\sqrt {{x^2} + {y^2}} > R} \right)} \end{array}} \right. $
(7) 式中, E0为常数,x, y, z为空间坐标,τ为脉冲持续时间(1/e2半宽),ω0为中心频率,R为光斑半径(高斯强度分布下为1/e2半径),φ为波前像差。对(5)式和(6)式进行傅里叶逆变换,可得入射脉冲的时域形状。模拟表明,波前像差φ(ω, x, y, z=0)项对飞秒脉冲时域分布的影响几乎可以忽略,故聚焦前脉冲的持续时间可直接对(5)式和(6)式中的exp[-τ2(ω-ω0)2/4]项进行傅里叶逆变换求解,其傅里叶逆变换为exp[-t2/τ2],式中t为时间,因此时域强度分布为exp[-2t2/τ2],可见τ即为脉冲持续时间(1/e2半宽)。根据瑞利-索末菲标量衍射理论,聚焦后飞秒脉冲场演化可以表示为[20]:
$ \begin{array}{*{20}{c}} {E\left( {\omega ,{x^\prime },{y^\prime },z} \right) = \frac{1}{{{\rm{i}}\lambda }}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } E } (\omega ,x,y,z = 0) \times }\\ {\exp \left[ { - \frac{{{\rm{i}}k\left( {{x^2} + {y^2}} \right)}}{{2f}}} \right]\frac{{\exp \left( {{\rm{i}}k{r_{\rm{d}}}} \right)}}{{{r_{\rm{d}}}}}\cos {\theta _{\rm{d}}}{\rm{d}}x{\rm{d}}y} \end{array} $
(8) 式中,(x′, y′)为传输距离z处的空间坐标,f为抛物面镜焦距,λ为激光波长,k为激光波数(2π/λ),rd为衍射距离,θd为衍射角,它们分别表示为:
$ {r_{\rm{d}}} = \sqrt {{{\left( {{x^\prime } - x} \right)}^2} + {{\left( {{y^\prime } - y} \right)}^2} + {z^2}} $
(9) $ \cos {\theta _{\rm{d}}} = z/{r_{\rm{d}}} $
(10) 对(8)式进行数值求解,可求得衍射距离z处的频域复振幅分布E(ω, x′, y′, z),再对其进行傅里叶逆变换,可得时域电场:
$ \begin{array}{*{20}{c}} {E\left( {t,{x^\prime },{y^\prime },z} \right) = }\\ {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_{ - \infty }^{ + \infty } E \left( {\omega ,{x^\prime },{y^\prime },z} \right)\exp ( - {\rm{i}}\omega t){\rm{d}}\omega } \end{array} $
(11) 因此, 衍射距离z处在一个光周期T的平均强度分布为:
$ I\left( {{x^\prime },{y^\prime },z} \right) = \frac{1}{T}\int_T {{{\left| {E\left( {t,{x^\prime },{y^\prime },z} \right)} \right|}^2}} {\rm{d}}t $
(12) 而I(x′, y′, z)正是所关心的聚焦强度分布。特别的,当z=f时,即为焦平面处的强度分布。
-
数值模拟中假定入射脉冲E0=1,脉冲持续时间τ=30fs,中心波长λ0=800nm(对应中心频率ω0=2.36rad·fs-1),光斑半径R=5mm,透镜焦距f=200mm,模式系数ck(ω0)=1,并且只考虑单个波前像差对聚焦光斑的影响。图 1中计算了均匀强度分布的飞秒脉冲在不同波前像差下焦平面处的光强分布。由图 1可见,在无像差的情况下,可获得半径约10μm的近衍射极限光斑。注意到图 1中即使在无像差情况下,聚焦光斑的外围也存在较弱的对称背景噪声,这是因为在数值模拟中,假定了入射脉冲的光强度均匀分布在直径10mm的范围内,因此入射光斑在透镜边缘存在较强的边缘衍射效应。可以预见,当入射脉冲具有高斯强度分布时,由于电场振幅1/e的衰减特性,当聚焦透镜尺寸足够大时,其边缘衍射效应几乎可以忽略,从而减小聚焦光斑外围由于衍射效应带来的强度噪声。从图 1可知,各类像差对均匀强度飞秒脉冲的聚焦光斑具有非常明显的不利影响,聚焦光斑的扭曲变形会导致聚焦峰值功率密度的降低。另外,注意到不同波前像差对应不同的聚焦光斑形态,比如k为7和8时的慧差与k为9和10时的三叶形像差,这也为聚焦光场是否存在像差或者何种像差占主导地位提供初步参考。

Figure 1. Intensity distribution at focal plane (f=200mm, z=f) of femtosecond pulse with homogenous intensity distribution under different kinds of aberration
图 2中计算了具有高斯强度分布的飞秒脉冲在不同波前像差下焦平面处的光强分布。与图 1相比,除了k=11的球差外,其它各类像差对焦平面处的光强分布影响很小。从图 2可知,当入射飞秒脉冲具有高斯强度分布时,即使存在一定量的波前像差,在焦平面处仍然有可能获得较好的聚焦光斑(当然这与波前像差的绝对量大小有关,即与模式系数ck(ω)的大小有关)。在k=11的球差情况下,焦平面处的聚焦光斑尺寸远大于其它像差情况下的光斑尺寸。后面的计算表明,在k=11的球差情况下,最小聚焦光斑并非位于焦平面,而在焦平面前约1mm的距离。

Figure 2. Intensity distribution at focal plane (f=200mm, z=f) of femtosecond pulse with Gaussian intensity distribution under different kinds of aberration
尽管相对于均匀强度分布的飞秒脉冲,波前像差对具有高斯强度分布的飞秒脉冲在焦平面处的光强分布形态影响要小,但计算表明,在不同的波前像差下,高斯强度飞秒脉冲的聚焦光斑光强分布形态在焦平面之前和焦平面之后还是具有比较明显的区别。图 3和图 4中分别计算了当聚焦焦距f=200mm时,聚焦光斑在焦平面前1mm和焦平面后1mm处的光强分布情况。为了与图 1和图 2进行对比,图 3和图 4的水平和竖直长度均与图 1、图 2一样,仍为60μm,这样可以对光斑的相对大小进行直接对比。从图 3和图 4可以明显地看出不同波前像差对光斑形态的影响。特别是在k为5和6的像散情况下,焦平面前的光斑形态与焦平面后对称位置处的光斑形态呈90°夹角,比如k=6时,焦平面前1mm处为水平椭圆光斑,而焦平面后1mm处变为竖直椭圆光斑,这也为聚焦时存在像散的情况提供了直接判断(对于大口径离轴抛物面镜聚焦飞秒脉冲时通常会存在像散)。

Figure 3. Intensity distribution before focal plane of 1mm (f=200mm, z=199mm) for femtosecond pulse with Gaussian intensity distribution under different kinds of aberration

Figure 4. Intensity distribution after focal plane of 1mm (f=200mm, z=201mm) for femtosecond pulse with Gaussian intensity distribution under different kinds of aberration
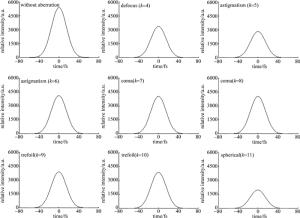
值得指出的是,针对数值模拟中采用的30fs(1/e2半宽度)脉冲,无论是均匀强度还是高斯强度分布,波前像差对脉冲持续时间(脉冲时域宽度)的影响都几乎可以忽略。图 5中给出了不同波前像差下,均匀强度分布的飞秒脉冲在聚焦焦平面中心位置处(对应图 1中x′=0, y′=0的中心位置)的脉冲时域强度波形(E(t, x′=0, y′=0, z=f)|2),图中横坐标为时间(单位为fs),纵坐标为相对强度。从图中可以看出,不同波前像差下与在没有像差情况下的脉冲持续时间几乎一样。而相对强度的大小表明只有在无像差的情况下,脉冲才具有最大的聚焦峰值功率。因此, 波前像差导致的聚焦峰值功率降低主要来自于对聚焦光强分布(光斑形态)的影响,而非来自于对脉冲持续时间的影响。
-
研究了在不同波前像差下具有均匀强度分布和高斯强度分布的飞秒脉冲的聚焦特性。对比焦平面处的光强分布,波前像差对均匀强度分布飞秒脉冲聚焦特性的影响比高斯强度分布的飞秒脉冲要明显。对于高斯强度分布的飞秒脉冲,计算表明,各类波前像差对焦平面前和焦平面后的光强分布具有较为明显的影响,使光强分布形态变差。因此对于高斯强度分布的飞秒脉冲,即使在焦平面处有可能获得较好的聚焦光斑,波前像差的存在也不利于在焦点处获得稳定的、较长的光束传播距离。尽管在实际的聚焦光学系统中,可能会同时存在多种波前像差,使飞秒光束的聚焦特性变得更为复杂,但是本文中的研究仍然对超短飞秒激光束的光束质量评估及聚焦特性分析具有实际的参考和指导意义。
波前像差对超短飞秒激光脉冲聚焦特性的影响
Effect of wavefront aberration on focusing characterisitics of ultrashort femtosecond laser pulses
-
摘要: 为了研究波前像差对超短飞秒激光脉冲聚焦特性的影响, 基于瑞利-索末菲标量衍射理论, 对比研究了在散焦、像散、慧差、三叶形像差以及球差等各类波前像差下, 均匀强度分布和高斯强度分布的超短飞秒激光脉冲的聚焦特性。结果表明, 波前像差对均匀强度分布的飞秒脉冲在焦平面处的光强分布具有明显的不利影响, 从而降低飞秒脉冲的聚焦峰值功率, 而对高斯强度分布的飞秒脉冲影响相对较小, 即在高斯强度分布下, 在焦平面处仍然有可能获得较好的、近衍射极限的聚焦光斑; 在非焦平面处, 即使初始脉冲具有高斯强度分布, 非焦平面处的光强分布受各类波前像差的影响也较为明显; 对于所研究的30fs(1/e2半宽度)超短脉冲, 波前像差对脉冲持续时间的影响几乎可以忽略。此研究结果对超短飞秒激光束的光束质量评估及聚焦特性分析具有实际的指导意义。Abstract: In order to study effect of wavefront aberration on focusing characteristics of ultrashort femtosecond laser pulses, based on Rayleigh-Sommerfeld scalar diffraction theory, focusing characteristics of ultrashort femtosecond laser pulses with uniform intensity distribution and Gaussian intensity distribution were compared and studied under different wavefront aberration, such as defocusing, astigmatism, coma aberration, trilobe aberration and spherical aberration. The results show that, wavefront aberration has an obvious adverse effect on intensity distribution of femtosecond pulses with uniform intensity distribution at the focal plane. The peak power of focusing femtosecond pulses is reduced. However, the influence of femtosecond pulses with Gaussian intensity distribution is relatively small. Under Gaussian intensity distribution, it is still possible to obtain better focusing spot near diffraction limit at focal plane. At the non-focal plane, even if the initial pulse has Gaussian intensity distribution, intensity distribution at the non-focal plane is also affected by various wavefront aberration. For 30fs (1/e2 half width) ultrashort pulse in this paper, the effect of wavefront aberration on pulse duration is almost negligible. The results are of practical significance for the evaluation of beam quality and the analysis of focusing characteristics of ultrashort femtosecond laser beams.
-
Key words:
- ultrafast optics /
- focusing /
- wavefront aberration /
- pulse duration /
- diffraction theory
-
Table 1. Zernike polynomial and the corresponding primary aberration
k n m Zk(ρ, θ) aberration 4 2 0 $\sqrt{3}$(2 ρ2-1) defocus 5 2 -2 $\sqrt{6}$ ρ2sin(2 θ) astigmatism 6 2 2 $\sqrt{6}$ ρ2cos(2 θ) astigmatism 7 3 -1 $\sqrt{8}$(3ρ2-2ρ)sin θ coma 8 3 1 $\sqrt{8}$(3ρ2-2ρ)cos θ coma 9 3 -3 $\sqrt{8}$ ρ3sin(3 θ) trefoil 10 3 3 $\sqrt{8}$ ρ3cos(3 θ) trefoil 11 4 0 $\sqrt{5}$ (6ρ4-6ρ2+1) spherical -
[1] YU T J, LEE S K, SUNG J H, et al. Generation of high-contrast, 30fs, 1.5PW laser pulses from chirped-pulse amplification Ti:sapphire laser [J]. Optics Express, 2012, 20(10): 10807-10815. doi: 10.1364/OE.20.010807 [2] CHU Y X, GAN Z B, LIANG X Y, et al. High-energy large-aperture Ti:sapphire amplifier for 5PW laser pulses [J]. Optics Letters, 2015, 40(21): 5011-5014. doi: 10.1364/OL.40.005011 [3] MOUROU G A, TAJIMA T, BULANOV S V. Optics in the relativistic regime [J]. Review of Modern Physics, 2006, 78(2): 309-371. doi: 10.1103/RevModPhys.78.309 [4] DAIDO H, NISHIUCHI M, PIROZHKOV A S. Review of laser-driven ion sources and their applications [J]. Reports on Progress in Physics, 2012, 75(5): 056401. doi: 10.1088/0034-4885/75/5/056401 [5] HAFZ N M, CHOI I W, SUNG J H, et al. Dependence of the electron beam parameters on the stability of laser propagation in a laser wakefield accelerator [J]. Applied Physics Letters, 2007, 90(15): 151501. doi: 10.1063/1.2721119 [6] THOMAS A G R, NAJMUDIN Z, MANGLESS S P D, et al. Effect of laser-focusing conditions on propagation and monoenergetic electron production in laser-wakefield accelerators [J]. Physics Review Letters, 2007, 98(9): 095004. doi: 10.1103/PhysRevLett.98.095004 [7] CHENG J, QIN X W, CHENG B, et al. Experimental investigation on focal spot measurement by schlieren method [J]. High Power Laser and Particle Beams, 2006, 18(4): 612-614 (in Chinese). [8] WU Y Ch, HE Y L, ZHU B, et al. Measurement of femtosecond laser focusing spot by optical imaging and pinhole method [J]. High Power Laser and Particle Beams, 2010, 22(12): 2871-2874 (in Chinese). doi: 10.3788/HPLPB20102212.2871 [9] JING Ch R, WANG Zh H, CHENG Y. Three dimensional micro-and nano-machining based on spatio temporal focusing technique of femtosecond laser [J]. Laser & Optoelectronic Progress, 2017, 54(4): 040005 (in Chinese). [10] LIANG D Zh, WANG M, DU Ch L, et al. Research on microchannel of silica glass fabricated by laser-induced backside wet etching [J]. Laser Technology, 2017, 41(2): 174-177 (in Chinese). [11] ZHANG W, ZHANG X B, FENG Q, et al. Effect of lens and gas on femtosecond laser machining in a nickel-based surperalloy [J]. Aeronautical Science & Technology, 2015, 26(11): 109-113 (in Chinese). [12] GONZÁLEZ-GALICIA M A, ROSETE-AGUILA M, GARDUÑO-MEJÍA J, et al. Effects of primary spherical aberration, coma, astigmatism and field curvature on the focusing of ultrashort pulses: Homogenous illumination [J]. Journal of the Optical Society of America, 2011, A28(10): 1979-1989. [13] GONZÁLEZ-GALICIA M A, GARDUN~O-MEJÍA J, ROSETE-AGUILA M, et al. Effects of primary spherical aberration, coma, astigmatism, and field curvature on the focusing of ultrashort pulses: Gaussian illumination and experiment [J]. Journal of the Optical Society of America, 2011, A28(10): 1990-1994. [14] LI H F, XIE H M, ZHANG Ch, et al. Studying the combined effects of primary aberraions on gaussian beam in high NA focusing system [J]. Acta Photonica Sinaca, 2015, 44(9): 0912001(in Chinese). doi: 10.3788/gzxb20154409.0912001 [15] SUN W Ch, YI W J, ZHANG Y D, et al. Experimental research on tight focus of femtosecond radially polarized light [J]. Acta Photonica Sinaca, 2015, 44(4): 0426001(in Chinese). doi: 10.3788/gzxb20154404.0426001 [16] ZHANG Y D, LI X J, JIA H, et al. Numeirical modelling of the focusing features for few-cycle radially polarized femtosecond pulses [J]. Acta Photonica Sinaca, 2015, 44(4): 0426002(in Chinese). doi: 10.3788/gzxb20154404.0426002 [17] SHELDAKOVA J, KUDRYASHOV A, CHEREZOVA T Y. Femtosecond laser beam improvement:Correction of parabolic mirror aberrations by means of adaptive optics[J]. Proceedings of the SPIE, 2008, 6872: 687203. doi: 10.1117/12.774089 [18] CHEN L X, HU X Ch, HAN K, et al. Improvement method for fitting high-frequency phase by zernike polynomials [J]. Acta Optica Sinica, 2016, 36(3): 0314001(in Chinese). doi: 10.3788/AOS201636.0314001 [19] NOLL R J. Zernike polynomials and atmosphere turbulence [J]. Journal of the Optical Society of America, 1976, 66(3): 207-211. doi: 10.1364/JOSA.66.000207 [20] SUN B Sh, SALTER P S, BOOTH M J. Effects of aberrations in spatiotemporal focusing of ultrashort laser pulses [J]. Journal of the Optical Society of America, 2014, A31(4): 765-772. [21] LIU Z Y, LI L, HU B T. Focusing property for ultra-short pulse laser reflected by off-axis parabolic mirrors [J]. Laser Technology, 2012, 36(5): 657-661(in Chinese). -


 网站地图
网站地图

 下载:
下载: