-
雪崩光电二极管(avalanche photodiode,APD)因其重量轻、体积小、能耗低、灵敏度高、响应速度快等优点而被广泛应用于各类激光探测设备。在APD激光主动探测系统的工作过程中,激光在大气中的传输过程及APD对激光的探测过程都影响着系统最终输出电流的特征[1-2]。BARRIOS和DIOS提出用指数威布尔(exponential Weibull,EW)分布描述大气在各种湍流条件下并存在孔径平均效应时接收光功率的概率密度分布,并验证了其准确性[1]。PEPPAS利用gamma-gamma分布描述了在各种湍流下点接收机接收光强的起伏,取得了较好的效果[3]。LAFORCE研究了噪声对APD探测过程造成的影响以及APD探测器噪声的影响因素,通过冷却方式降低了等效噪声功率,提高了系统探测性能[4]。
国内外学者已对激光在大气中传输及APD对激光的探测分别进行了广泛研究,但目前为止,未见一个模型可将这两个过程综合考虑。针对该问题,从激光在大气中传输、APD对激光的探测两个过程入手,进行研究,建立了指数威布尔-高斯双重随机过程模型,并利用该模型对APD输出电流概率密度分布及其影响因素进行了研究。
-
APD探测系统的噪声主要来源有:背景光散粒噪声、信号光散粒噪声、暗电流噪声、热噪声、放大器噪声[5-6]。其中暗电流噪声又分为经过倍增的体漏电流散粒噪声和未经过倍增的表漏电流噪声[7]。APD探测系统的噪声可由下式表示:
$ \begin{array}{l} {{\bar I}_{\rm{n}}} = \left[ {2e{M^2}{F_{\rm{m}}}B\left( {\frac{{\eta e}}{{h\nu }}{P_{\rm{s}}} + \frac{{\eta e}}{{h\nu }}{P_{\rm{b}}} + {i_{\rm{d}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;2e{i_1}B + \left( {\frac{{4{k_{\rm{B}}}TB}}{R}} \right) + {i_{\rm{a}}}{]^{1/2}} \end{array} $
(1) 式中,e是电子电荷;M为APD的倍增因子;Fm为噪声因子;Ps为探测器接收的信号功率;B为接收系统带宽;Pb为入射背景光功率;η为APD的量子效率;h为普朗克常数;ν为光波频率;kB为玻尔兹曼常数;T为绝对温度;R为等效负载电阻;id为体漏电流;il为表面漏电流;ia为放大器噪声。其中,等式右边第1项为信号光、背景光、体漏电流的散粒噪声,第2项为表漏电流噪声,第3项为探测系统热噪声,第4项为放大电路噪声。
从微观量子角度分析,直接探测型探测器输出噪声可用泊松分布进行准确描述[8]。而在光量子极限工作条件下,系统接收大量光子并产生大量电子时,可按照经典的统计分布来描述。根据上述条件,结合中心极限定理,APD探测系统输出的噪声与信号电流之和呈高斯分布。假设APD接收端面接收的信号为稳定信号Is,有激光回波时噪声电流均方根为In,则信号和噪声之和为:
$ I = {I_{\rm{s}}} + {I_{\rm{n}}} $
(2) 其概率密度函数为:
$ {f_{\rm{c}}}(I) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {I_{\rm{n}}}}}\exp \left( { - \frac{{I - {I_{\rm{s}}}}}{{2{I_{\rm{n}}}^2}}} \right) $
(3) -
激光在大气中传输受到激光大气传输效应的影响。激光传输大气传输效应主要包括:湍流效应、衰减效应、热晕效应[9-10]。对于激光主动探测装备,大气湍流和大气衰减都会对装备出射的激光在大气中的传输效果产生明显影响。
大气对激光的衰减主要表现在吸收和散射两个方面。对于大气中传输的激光,米氏散射是造成其衰减的主要原因。当气象条件为晴朗、霾、雾时,大气的综合衰减系数一般可表示为[11]:
$ \omega = \left( {\frac{{3.91}}{{{R_{\rm{v}}}}}} \right){\left( {\frac{\lambda }{{0.55}}} \right)^{ - q}}{\rm{k}}{{\rm{m}}^{ - 1}} $
(4) 式中,Rv为大气能见度,单位是km;λ是入射光波长,单位为μm;q是与波长有关的常数。
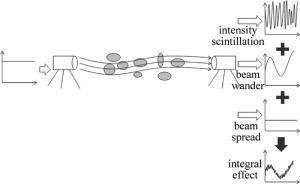
大气湍流运动是由大气密度随机变化导致的大气折射率变化而引起的[12]。大气湍流会使光斑空间位置随时间变化、接收端面光强随时间起伏、光斑面积和半径变化,主要表现为光束漂移、光强闪烁和光束扩展等大气湍流效应,严重影响装备对激光的探测[13]。
如图 1所示,光强闪烁导致接收机探测到的光强在时间、空间上随机起伏,光束漂移导致的对准误差将会加剧这种起伏,光束扩展会使接收的光功率减小。
-
由gamma-gamma分布模型可知,接收光的功率是由符合gamma分布的大尺度起伏与小尺度起伏联合调制的结果。归一化光强Ig=IxIy,Ix和Iy分别为大尺度湍流和小尺度湍流引起光强随机起伏过程,两者统计独立,且都服从gamma分布[3]。光强Ig的概率密度函数可表示为:
$ {f_{{\rm{GG}}}}\left( {{I_{\rm{g}}}} \right) = \frac{{2{{(\alpha \beta )}^{\frac{{\alpha + \beta }}{2}}}}}{{\Gamma (\alpha )\Gamma (\beta ){I_{\rm{g}}}}}{{\rm{K}}_{\alpha - \beta }}\left( {2\sqrt {\alpha \beta {I_{\rm{g}}}} } \right) $
(5) 式中,α, β分别为与大尺度湍流、小尺度湍流相关的系数;Γ(x)是gamma函数;Kμ(x)为μ阶第2类修正贝塞尔函数。
-
当接收光功率起伏服从指数威布尔分布时,其概率密度函数为[14]:
$ \begin{array}{l} {f_{{\rm{EW}}}}\left( {{I_{\rm{g}}}} \right) = \frac{{{\alpha ^\prime }{\beta ^\prime }}}{{{\eta ^\prime }}}{\left( {\frac{{{I_{\rm{g}}}}}{{{\eta ^\prime }}}} \right)^{{\beta ^\prime } - 1}}\exp \left[ { - {{\left( {\frac{{{I_{\rm{g}}}}}{{{\eta ^\prime }}}} \right)}^{{\beta ^\prime }}}} \right] \times \\ \;\;\;\;\;{\left\{ {1 - \exp \left[ { - {{\left( {\frac{{{I_{\rm{g}}}}}{{{\eta ^\prime }}}} \right)}^{{\beta ^\prime }}}} \right]} \right\}^{{\alpha ^\prime } - 1}}, \;\left( {{I_{\rm{g}}} > 0} \right) \end{array} $
(6) 式中,α′, β′为形状参量,决定分布曲线的形状;η′为尺度参量,主要决定曲线的陡峭度。
$ {\alpha ^\prime } = 3.931{\left( {\frac{D}{{{\rho _0}}}} \right)^{ - 0.519}} $
(7) $ {\beta ^\prime } = {\left( {{\alpha ^\prime }{\sigma _I}^2} \right)^{ - 6/11}} $
(8) $ {\eta ^\prime } = \frac{1}{{{\alpha ^\prime }\Gamma \left( {1 + \frac{1}{{{\beta ^\prime }}}} \right)g\left( {{\alpha ^\prime }, {\beta ^\prime }} \right)}} $
(9) $ g\left( {{\alpha ^\prime }, {\beta ^\prime }} \right) = \sum\limits_{i = 0}^\infty {\frac{{{{( - 1)}^i}{{(i + 1)}^{ - \frac{{1 + {\beta ^\prime }}}{{{\beta ^\prime }}}}}\Gamma \left( {{\alpha ^\prime }} \right)}}{{i!\Gamma \left( {{\alpha ^\prime } - i} \right)}}} $
(10) 式中,D为接收口径;ρ0为大气相干半径;σI2为闪烁指数。因此可知,指数威布尔分布的参量可以通过探测器参量、大气参量、闪烁指数直接计算获得。
大气相干半径ρ0的表达式如下:
$ {\rho _0} = {\left( {1.46{C_n}^2{k^2}L} \right)^{ - 3/5}} $
(11) 式中,Cn2为大气折射率结构常数,k为波数,L为探测距离。当探测器对激光进行探测时,将ρ0>D时的接收情形看作点接收情况,当ρ0<D时则考虑孔径平均效应。点接收情况下,探测器接收光功率起伏的概率密度分布可用gamma-gamma较好地进行描述。而当孔径平均效应存在时,指数威布尔分布则对于各种强度的湍流下的概率密度分布具有较好描述效果[15]。
-
当强度在时间与空间上稳定不变的激光入射到探测器时,探测器输出的电流概率密度分布可用高斯函数描述。但在实际应用中,任何强度随机涨落的影响因素都将导致入射到探测器表面上激光强度具有随机性。因此,必须将(3)式中的高斯分布fc(I)看作条件概率分布fc(I|Is),并且一般激光主动探测设备对激光探测时都存在孔径平均效应,所以Is的先验概率密度分布可用指数威布尔分布表示。
探测器对经过湍流大气的激光进行探测并输出电流的过程包含两个随机过程,且其中一个随机过程中的某一参量以另一随机过程为条件,这与Mandel公式成立条件极为相似[16]。Mandel公式为:
$ P(K) = \int_0^\infty {\frac{{{{\left( {a{I_{\rm{g}}}} \right)}^K}}}{{K!}}} \exp \left( { - a{I_{\rm{g}}}} \right)P\left( {{I_{\rm{g}}}} \right){\rm{d}}{I_{\rm{g}}} $
(12) 式中,P(K)为光电事件出现K次的概率,K为光电事件个数,a为常数。Mandel公式是根据光与物质作用的半经典理论提出的,描述光电事件出现概率的公式。该公式中包含的两个随机过程为:光强的随机起伏的随机过程,光与光敏物质作用释放出电子的泊松随机过程,并且Ig的先验概率为P(Ig)。虽然Mandel公式描述的一个离散过程,求解出来的是一个概率值,APD对激光探测并输出电流描述的是一个连续过程,需解出概率密度分布,但两者基于相同的数学条件,因此参考Mandel公式提出的思想与形式,建立指数威布尔-高斯双重随机过程,将探测器输出电流的无条件概率密度函数表示为:
$ f(I) = \int_0^\infty {{f_{\rm{c}}}} \left( {I|{I_{\rm{s}}}} \right){f_{{\rm{EW}}}}\left( {{I_{\rm{s}}}} \right){\rm{d}}{I_{\rm{s}}} $
(13) 将(3)式、(6)式带入(13)式可得:
$ \begin{array}{l} f(I) = \int_0^\infty {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {I_n}}}} \exp \left( { - \frac{{I - {I_{\rm{s}}}}}{{2{I_{\rm{n}}}^2}}} \right)\frac{{{\alpha ^\prime }{\beta ^\prime }}}{{{\eta ^\prime }}}{\left( {\frac{{{I_{\rm{s}}}}}{{{\eta ^\prime }}}} \right)^{{\beta ^\prime } - 1}} \times \\ \;\;\;\exp \left[ { - {{\left( {\frac{{{I_{\rm{s}}}}}{{{\eta ^\prime }}}} \right)}^{{\beta ^\prime }}}} \right]{\left\{ {1 - \exp \left[ { - {{\left( {\frac{{{I_{\rm{s}}}}}{{{\eta ^\prime }}}} \right)}^{{\beta ^\prime }}}} \right]} \right\}^{{\alpha ^\prime } - 1}}{\rm{d}}{I_{\rm{s}}} \end{array} $
(14) 通过(14)式即可将激光在大气中的传输过程及APD对激光的探测过程两个随机过程放在一个模型中进行分析。
-
在APD探测系统对目标的探测过程中,APD输出信噪比、大气折射率结构常数、探测器口径、探测距离等因素都会对APD输出电流的概率分布产生影响。
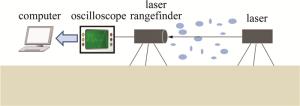
在某一大气条件下,通过如图 2所示的实验装置对APD探测经大气传输的激光后输出的电流进行测量。将某型激光测距机进行改装,通过外置电源仅对其APD探测系统供电,使其偏压恒定,利用示波器采集其输出电流,并将电流数据传入计算机,利用数学软件计算输出电流的概率密度分布。同时,通过对某时刻激光在大气中传输的光强起伏方差进行记录,测量该时刻的大气折射率结构常数[17],由此计算相关大气参量,并对双随机过程进行仿真计算,与实验中所得数据进行对比。实验中所用激光波长为1064nm,出射能量80mJ,发散角0.7mrad,初始半径25mm,激光测距机所用APD型号为C30950E,探测口径40mm,接收光学系统视场0.95mrad,实验距离730m,同时为方便计算,将Is进行标准化处理,即令I=Is/〈Is〉,使〈I〉=1,其中〈〉表示取平均值。
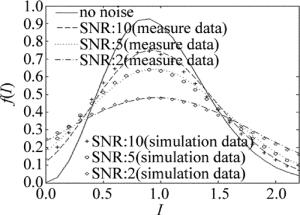
在激光器前放置不同衰减片,使APD电流输出信噪比(signal-to-noise ratio,SNR)不同,同时用示波器采集APD探测系统的输出电流,通过数学软件计算电流的概率密度,并与仿真数据进行对比。图 3为不同信噪比下APD输出电流概率密的曲线。保持APD接收的信噪比不变,在不同时刻测量APD输出电流的概率密度分布,同时测量相应时刻下的大气折射率结构常数,对双随机探测过程进行仿真。图 4即为不同大气折射率结构常数下的APD输出电流的概率密度曲线。表 1中为实验相关参量及计算所得数据。其中β02为Rytov指数,x为平均值,D(x)为归一化输出电流的方差,偏移量为x-1。

Figure 4. Probability density curve of APD output current at different atmospheric refractive index structure constants
Table 1. Experiment related parameters and the calculated data
No. SNR Cn2/m2/3 σI2 ρ0/mm β02 x D(x) 1 10 3×10-14 0.1742 14.67 0.5432 1.0029 0.2781 2 5 3×10-14 0.1742 14.67 0.5432 1.0109 0.3565 3 2 3×10-14 0.1742 14.67 0.5432 0.9500 0.5354 4 10 2.5×10-15 0.0181 65.14 0.0472 1.0002 0.1198 5 10 3×10-14 0.1742 14.67 0.5432 1.0029 0.2781 6 10 4.9×10-14 0.3034 10.81 0.9049 1.0039 0.4035 由图 3、图 4可看出,仿真数据与实验测量结果基本一致,其中存在的误差主要是由于测量大气折射率结构常数时的误差导致。
结合表 1,由图 3可知,当APD输出的信噪比不同时,其输出电流的概率密度将产生很大变化。当信噪比降低时,概率密度的峰值会减小,强度较小和较大的I概率将会增大,同时输出电流平均值偏离信号电流程度增大,方差增大,数据离散程度将会加剧。结合表 1,由图 4可知,大气折射率结构常数变化时,闪烁系数、大气相干半径等参量都会发生变化,进而使光强在接收端上的起伏的概率密度发生改变,最终导致APD输出的电流发生变化。随着大气折射率结构常数的增大,概率密度曲线峰值减小并稍向左移,曲线趋于平缓,平均值偏离信号程度增大,数据离散程度加大。
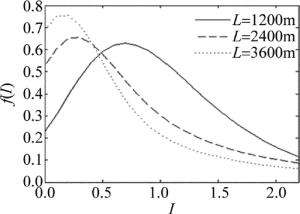
由于实验条件限制,对不同接收口镜、不同探测距离下APD的双重随机探测过程仅进行了仿真分析。表 2为相关仿真参量。图 5为不同接收口径下APD输出电流的概率密度曲线。图 6为不同距离下APD输出电流的概率密度曲线。
Table 2. The related parameters of numerical simulation
parameters value λ 1064mm SNR 10 D 40mm Cn2 3×10-14m2/3 在仿真所选取的大气条件下,大气相干半径ρ0=0.014mm,当接收口径D<ρ0时, 可看作点接收情况; 当D>ρ0时,则应该考虑孔径平均效应。由图 5可知,随着接收口径的增大,概率密度曲线峰值会增大并右移。但是接收口径在一定范围内变化时,无论有无孔径平均效应,对概率密度曲线影响都不大。由图 6可知,探测距离改变对电流的概率密度曲线影响显著,随着探测距离增大,输出电流偏离信号程度逐渐增大。
-
通过对激光在大气中的传输及APD对激光探测两个过程进行研究,构建了可将大气湍流及APD特性同时考虑的指数威布尔-高斯双重随机过程模型。通过实验测量了不同信噪比、不同湍流下APD输出电流的概率密度曲线,并对不同口径、不同探测距离下APD的输出进行了仿真。实验结果表明,信噪比及湍流的变化会使输出电流的平均值偏移增大,离散程度加剧,同时实验数据与仿真数据具有较好一致性,仿真数据表明,探测口径变化时概率密度曲线变化不明显,而探测距离改变时输出电流离散程度虽未明显变大,但偏移现象明显。因此得出结论:APD接收信噪比、大气折射率结构常数、探测距离的变化对APD的双重随机探测过程影响明显,而接收口径的变化对APD的双重随机探测过程的影响则较弱。
APD对湍流大气中激光的双重随机探测过程
Dual stochastic detection process for APD receiving laser in turbulent atmosphere
-
摘要: 为了研究雪崩光电二极管(APD)对大气传输后的激光进行探测时, 所受大气湍流效应及APD噪声的影响, 分析了激光在湍流大气中传输、APD对激光探测两个过程, 结合APD的探测原理, 建立了指数威布尔-高斯双重随机过程模型。通过实验测量了不同信噪比、不同大气湍流下APD输出电流的概率密度, 对探测距离不同、接收口径不同的情况进行了仿真。结果表明, 接收信噪比为2, 5, 10时, 光强分布方差分别为0.5354, 0.3565, 0.2781, 偏移量分别为0.05, 0.0109, 0.0029;大气折射率结构常数为2.5×10-15, 3×10-14, 4.9×10-14时, 方差分别为0.1198, 0.2781, 0.4035, 偏移量分别为0.0002, 0.0029, 0.0039;双重随机过程模型可准确描述经过大气传输的激光被APD探测的过程; 探测器口径的变化对APD输出电流的概率密度影响不大, 而接收信噪比、探测距离、大气折射率结构常数的增大会使APD输出电流平均值较信号电流产生较大偏移、且离散程度加剧。该模型的建立对激光探测技术研究具有一定的参考价值。Abstract: In order to study effect of atmospheric turbulence and avalanche photodiode (APD) noise when an APD receiving laser transmitted in turbulent atmosphere, both processes, i.e., laser propagation in turbulent atmosphere and laser detection by APD were analyzed. Then, combined with the detection principle of APD, the exponential Weibull-Gauss dual stochastic process model was established. The probability density of APD output current under different signal-to-noise ratios and atmospheric turbulence was measured. Different detection distances and receiving apertures were simulated. The results show that, when the received signal-to-noise ratio is 2, 5 and 10, the variances of light intensity distribution are 0.5354, 0.3565 and 0.2781, respectively and the offsets are 0.05, 0.0109 and 0.0029, respectively. When the structure constants of atmospheric refractive index are 2.5×10-15, 3×10-14, 4.9×10-14, the variances are 0.1198, 0.2781 and 0.4035, respectively and the offsets are 0.0002, 0.0029 and 0.0039, respectively. The dual stochastic process model can accurately describe the process for APD detecting laser transmitting in turbulent atmosphere. The change of detector aperture has little effect on the probability density of APD output current. With the increase of the received signal-to-noise ratio, detection distance and atmospheric refractive index structure constant, the average output current of APD is larger than that of signal current. And the degree of dispersion is aggravated. The establishment of this model has a certain reference value for the research of laser detection technology.
-
Table 1. Experiment related parameters and the calculated data
No. SNR Cn2/m2/3 σI2 ρ0/mm β02 x D(x) 1 10 3×10-14 0.1742 14.67 0.5432 1.0029 0.2781 2 5 3×10-14 0.1742 14.67 0.5432 1.0109 0.3565 3 2 3×10-14 0.1742 14.67 0.5432 0.9500 0.5354 4 10 2.5×10-15 0.0181 65.14 0.0472 1.0002 0.1198 5 10 3×10-14 0.1742 14.67 0.5432 1.0029 0.2781 6 10 4.9×10-14 0.3034 10.81 0.9049 1.0039 0.4035 Table 2. The related parameters of numerical simulation
parameters value λ 1064mm SNR 10 D 40mm Cn2 3×10-14m2/3 -
[1] BARRIOS R, DIOS F. Exponentiated Weibull distribution family un-der aperture averaging for Gaussian beam waves [J]. Optics Express, 2012, 20(12): 13055-13064. doi: 10.1364/OE.20.013055 [2] WANG Y, LÜ Y, WANG Y, et al. Noise characterization of geiger-mode 4H-SiC avalanche photodiodes for ultraviolet single-photon detection[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2017, 24(2):3800305. [3] PEPPAS K P. A simple, accurate approximation to the sum of gamma-gamma variates and applications in MIMO free-space optical systems[J].IEEE Photonics Technology Letters, 2011, 23(13):839-841. doi: 10.1109/LPT.2011.2135342 [4] LAFORCE F. Low noise optical receiver using Si-APD[J]. Proceedings of the SPIE, 2009, 7212:523-534. [5] MEGIE G. Laser remote sensing: Fundamentals and applications[J]. Eos Transactions American Geophysical Union, 2013, 66(40):686. [6] WANG W, BAO X Y, CHEN L, et al. High detection efficiency CMOS single photon avalanche diode device[J]. Acta Photonica Sinica, 2016, 45(8): 0823001(in Chinese). doi: 10.3788/gzxb [7] ZHANG J H, ZHENG Y Ch, SHANG W D, et al. Research of space-based photon counting laser detection for space debris[J]. Laser Technology, 2017, 41(3):312-317(in Chinese). [8] DAI Y J. Lidar principle[M]. Beijing: National Defense Industry Press, 2002:49-50 (in Chinese). [9] RAO R Zh. Modern atmospheric optics [M]. Beijing: Science Press, 2012: 76-77(in Chinese). [10] ZHANG L, LI B, ZHAO X, et al. Influence of atmospheric turbulence on space laser communication tracking system[J]. Acta Photonica Sinica, 2017, 46(9): 0901001(in Chinese). doi: 10.3788/gzxb [11] LIU M, WANG H X, WANG Q, et al. Modified model for calculation of atmospheric attenuation under rain and fog coexistence weather[J].Journal of Chinese Lasers, 2011, 38(10): 1005002(in Ch-inese). doi: 10.3788/CJL [12] XU G Y, WU J, YANG Ch P, et al. Numerical simulation and intensity fluctuation of Gaussian beam in atmospheric turbulence[J]. Laser Technology, 2008, 32(5): 548-550 (in Chinese). [13] PIERCE J. Optical channels: Practical limits with photon counting[J]. IEEE Transactions on Communications, 1978, 26(12):1819-1821. doi: 10.1109/TCOM.1978.1094043 [14] VETELINO F S, YOUNG C, ANDREWS L, et al. Aperture averaging effects on the probability density of irradiance fluctuations in moderate-to-strong turbulence[J]. Applied Optics, 2007, 46(11):2099-2108. doi: 10.1364/AO.46.002099 [15] YAN Y H, WEN Y, LIU B Q. Probability distribution characteristics of received power scintillation in laser atmosphere transmission[J]. Laser and Infrared, 2016, 46(4): 400-405(in Chinese). [16] MANDEL L. Fluctuations of photon beams and their correlations[J]. Proceedings of the Physical Society, 1958, 72(6):1037-1048. doi: 10.1088/0370-1328/72/6/312 [17] CHEN C Y, YANG Y M, GENG Sh F, et al. Experiment and analysis of laser refractive index structure constant measurement[J]. Infrared and Laser Engineering, 2006, 35(s1): 422-426(in Ch-inese). -


 网站地图
网站地图

 下载:
下载: