-
高光谱图像具有光谱分辨率高、波段数量多、光谱信息丰富等特点,被广泛应用于军事[1]、农业[2]、矿业[3]、渔业[4]、林业[5]等领域。在高光谱图像的众多应用中,分类是前提,其目标是给图像中的每个像元赋以唯一的类别标识。高光谱图像在为地物分类和识别提供了细致丰富的光谱信息的同时,其数据的高维性与谱间存在的大量冗余信息也给分类带来了困难。如果直接用高光谱数据对地物进行分类,容易产生Hughes现象,且计算量大、耗时长。为了克服这些困难,经常采用数据降维技术。
对于数据降维,学者们提出了许多方法,这些方法通常依据某种准则,将高维的谱向量投影到低维的特征空间,然后在低维特征空间进行分类。经典的线性降维方法有主成分分析(principal component analysis, PCA)和线性判别式分析(linear discriminant analysis, LDA)。PCA和LDA都是在高光谱数据满足全局线性的假设下通过寻找不同的线性模型进行降维,但高光谱数据往往是非线性的,因此,采用线性的PCA和LDA无法揭示其非线性结构。为了在提取的特征中揭示高光谱数据的非线性结构,研究者通过核函数将低维的线性空间映射到高维的非线性空间,然后进行数据降维。这些方法包括核主成分分析(kernel principal component analysis,KPCA)[6-7]、核Fisher判别式分析[8]、广义判别式分析[9]和支持向量机(support vector machines,SVM)。流形学习算法是另一种揭示样本非线性结构的方法。与基于核函数的方法相比较,流形学习算法通过邻接图的嵌入能够有效保留数据的局部结构信息[10-13]。
近来,稀疏表示分类器(sparse representation cla-ssification, SRC)被广泛应用[14-16]。与其它的分类器相比较,SRC不需要训练过程,而是用所有的训练样本组成一个字典,并通过稀疏最小化重构误差实现对测试样本的分类。由于对每一个测试样本都需要进行复杂的编码过程,因此,在数据量较大时,SRC的算法复杂度是巨大的。ZHANG等人[17]的研究表明,在对测试样本进行分类时,起主要作用的是所有样本对测试样本的协同表示而不是稀疏性约束,并提出一种基于l2范数编码的协同表示分类方法(collaborative representation based classification, CRC)。与基于l1范数编码的SRC相比较,这种基于l2范数的编码方法能够得到解析解,因此具有更小的计算复杂度,且在人脸识别与高光谱分类方面具有较高的识别性能[18-21]。最近,CAI等人从概率的角度出发,分析了CRC的机理并提出概率协同表示分类方法(probabilistic collaborative representation based classifier, ProCRC)[22],在MNIST数据库与AR数据库上取得了较好的识别结果。
上述方法在分类时仅仅考虑了像元的光谱信息,而从空间的角度来看,空间相邻的像元最有可能属于同一类,即具有空间一致性。为了充分利用像元的空间信息,近年来,研究者提出了许多空谱联合的高光谱图像的分类方法。这些方法在相似性度量和特征提取时考虑了像元的空间相关性,取得了优于纯光谱特征的分类精度[23-24]。因此,如何充分利用空间信息与光谱信息进行像元的分类,是高光谱图像分类的研究热点。
现有的大多数基于空谱信息的高光谱分类方法仅利用的是单个像元的光谱数据,而事实上高光谱遥感数据是通过光谱技术与成像技术相结合得到的,最终的光谱数据中可能存在高光谱传感器噪声、无光照时仪器自身带的暗电流、大气校正时的偏差等;在反射率计算时,混合像元、地形、光照等问题也会影响到最终的数据。由此可见,每个像元的光谱数据易受到噪声污染且不是孤立的,而是与其邻域其它像元紧密相关的。为了降低单个像元光谱数据对噪声的敏感性并充分利用近邻像元的光谱相似特点,本文中对每个像元的光谱数据用半径为r的圆形邻域内像元光谱数据生成的邻域谱代替,这样可有效克服噪声影响并充分利用空间信息。生成邻域谱后,再采用概率协同表示分类器进行分类。
-
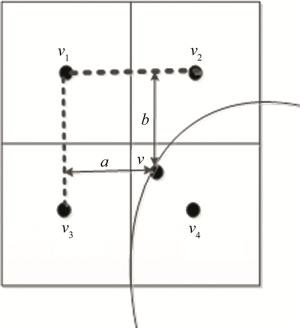
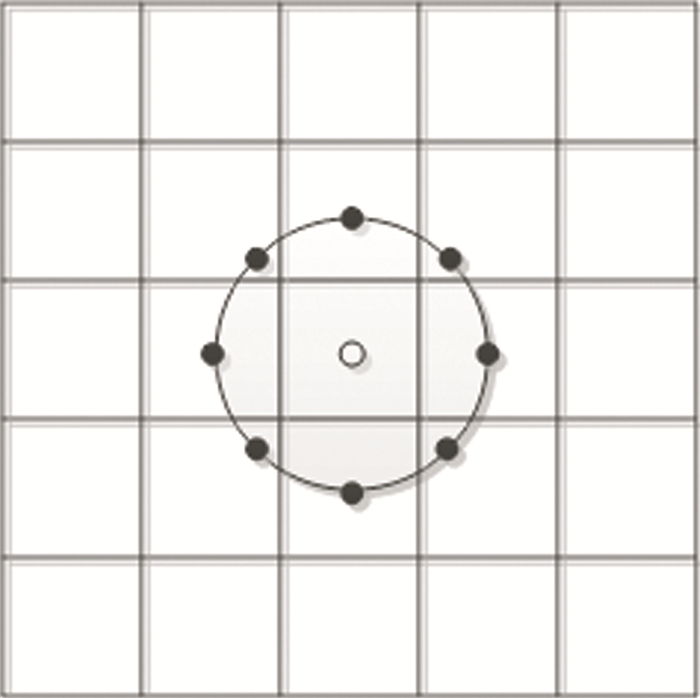
以坐标(i, j)为中心点的像元,图 1中给出了其半径为r的P个像元构成的邻域,表示为G(r, P)。P个邻域像元中,第m(m=1, …, P)个邻域点的坐标位置可通过下式计算:
$ \left\{ {\begin{array}{*{20}{l}} {{i_m} = i - r\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}m}}{P}} \right)}\\ {{j_m} = j - r\cos \left( {\frac{{2{\rm{ \mathsf{ π} }}m}}{P}} \right)} \end{array}} \right. $
(1) 当邻域点未落在像元中心位置时,其谱向量可通过双线性插值计算得到,如图 2所示。假定像元(i, j)的某个邻域像元为v,距离v最近的4个像元分别是v1, v2, v3和v4,且它们的谱向量分别为s1, s2, s3和s4,各点之间的距离为1个像素。假定像元v到点v1和点v3的水平距离为a,到点v2的垂直距离为b,则v的谱向量g可由下式计算得到:
$ \begin{array}{l} \mathit{\boldsymbol{g}} = {\mathit{\boldsymbol{s}}_1} \cdot (1 - a) \cdot (1 - b) + {\mathit{\boldsymbol{s}}_2} \cdot a \cdot (1 - b) + \\ \;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{s}}_3} \cdot (1 - a) \cdot b + {\mathit{\boldsymbol{s}}_4} \cdot a \cdot b \end{array} $
(2) 在计算得到像元(i, j)所有P个领域点的谱向量gi(i=1, …, P)后,若像元(i, j)谱向量为s,则其邻域谱$\mathit{\boldsymbol{\hat s}}$可由下式得到:
$ \mathit{\boldsymbol{\widehat s}} = \frac{1}{{P + 1}}\left( {\mathit{\boldsymbol{s}} + \sum\limits_{i = 1}^P {{\mathit{\boldsymbol{g}}_i}} } \right) $
(3) -
假定第i类训练样本表示为矩阵Xi=[xi, 1, xi, 2, …, xi, ni],向量xi, j∈Rd是第i类的第j个样本,则训练基共有N=c×n个样本,所有的训练样本集可表示为矩阵X=[X1, X2, …, Xc],Rd表示d子维空间,c是样本的类别数量,lX={1, 2, …, c}表示样本标签集合,并将全体训练样本张成的子空间S称为协同子空间。S空间中的样本向量x可表示为$\mathit{\boldsymbol{x}} = \mathit{\boldsymbol{X\alpha }} = \sum\limits_{i = 1}^c {{\mathit{\boldsymbol{X}}_i}} {\mathit{\boldsymbol{\alpha }}_i}$,其中向量α=[α1, α2, …, αc],αi是对应于Xi的编码。若l(x)表示样本x的标签,则样本x可由训练集中的样本协同地表示为$\mathit{\boldsymbol{x}} = \mathit{\boldsymbol{X\alpha }} = \sum\limits_{i = 1}^c {{\mathit{\boldsymbol{X}}_i}} {\mathit{\alpha }_i}$,其属于第i类的概率可表示为[22]:
$ \begin{array}{*{20}{c}} {P(l(\mathit{\boldsymbol{x}}) = i|l(\mathit{\boldsymbol{x}})) \in {l_\mathit{\boldsymbol{X}}} \propto }\\ {\exp \left( { - \mathit{\varepsilon }{{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{X}}_i}{\alpha _i}} \right\|}_2}^2} \right)} \end{array} $
(4) 式中,ε是一个常数。
对于待测样本y,其属于第i类的概率可表示为[22]:
$ \begin{array}{*{20}{c}} {P(l(\mathit{\boldsymbol{y}}) = i) \propto \exp \left[ { - \left( {{{\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{X\alpha }}} \right\|}_2}^2 + } \right.} \right.}\\ {\lambda {{\left\| \mathit{\boldsymbol{\alpha }} \right\|}_2}^2 + \gamma {{\left\| {\mathit{\boldsymbol{X\alpha }} - {\mathit{\boldsymbol{X}}_i}{\alpha _i}} \right\|}_2}^2)]} \end{array} $
(5) 式中, λ和γ是常数。α可由下式计算得到[22]:
$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\widehat \alpha }} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{\alpha }} \left\{ {\frac{\gamma }{c}\sum\limits_{k = 1}^c {{{\left\| {\mathit{\boldsymbol{X\alpha }} - {\mathit{\boldsymbol{X}}_k}{\alpha _k}} \right\|}_2}^2} + } \right.}\\ {\left. {\lambda {{\left\| \mathit{\boldsymbol{\alpha }} \right\|}_2}^2 + {{(\mathit{\boldsymbol{X\alpha }} - \mathit{\boldsymbol{y}})}^{\rm{T}}}{\mathit{\boldsymbol{W}}_x}(\mathit{\boldsymbol{X\alpha }} - \mathit{\boldsymbol{y}})} \right\}} \end{array} $
(6) 式中,Wx为对角矩阵,其对角元素为:
$ {\mathit{\boldsymbol{W}}_x}(i, i) = 1/\left( {\sum\limits_{j = 1}^N {{\mathit{\boldsymbol{X}}_{i, j}}} {\mathit{\alpha }_j} - {y_i}} \right) $
(7) 式中,Xi, j表示矩阵X的第i行第j列元素。
-
在得到解向量α后,可由(5)式得到样本y属于第i(i=1, …, c)类的概率:
$ \begin{array}{*{20}{c}} {P(l(\mathit{\boldsymbol{y}}) = i) \propto \exp \left[ { - \left( {{{\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{X}}\mathit{\boldsymbol{\widehat \alpha }}} \right\|}_2}^2 + } \right.} \right.}\\ {\left. {\left. {\lambda {{\left\| {\mathit{\boldsymbol{\widehat \alpha }}} \right\|}_2}^2 + \gamma {{\left\| {\mathit{\boldsymbol{X}}\mathit{\boldsymbol{\widehat \alpha }} - {\mathit{\boldsymbol{X}}_i}{{\hat \alpha }_i}} \right\|}_2}^2} \right)} \right]} \end{array} $
(8) 由(8)式可知,对所有的类,${\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{X}}\mathit{\boldsymbol{\widehat \alpha }}} \right\|_2}^2 + \lambda {\left\| {\mathit{\boldsymbol{\widehat \alpha }}} \right\|_2}^2$是相同的,因此,样本y属于第i类的概率可表示为:
$ {P_i} = \exp \left( { - {{\left\| {\mathit{\boldsymbol{X}}\mathit{\boldsymbol{\widehat \alpha }} - {\mathit{\boldsymbol{X}}_i}{{\hat \alpha }_i}} \right\|}_2}^2} \right) $
(9) 这样,样本y的类别归属由下式表示的规则决定:
$ l(\mathit{\boldsymbol{y}}) = \mathop {\max }\limits_i \left\{ {{P_i}} \right\} $
(10) -
实验中选取美国印第安纳西北地区的Indian Pines高光谱图像和美国加州的萨利纳斯山谷的高光谱图像Salinas scene,利用总体识别率和kappa值作为分类性能的评价指标,并和主成分分析(PCA)、支持向量机(SVM)、基于稀疏表示的分类器(SRC)、基于协同表示的分类器(CRC)方法进行性能比较。
-
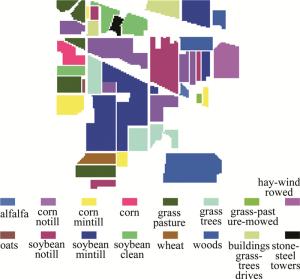
Indian Pines图像大小为145pixel×145pixel,波长范围为400nm~2500nm,光谱分辨率为10nm。原始波段数为224个,去除坏波段和和水体吸收波段,用剩余的200个波段进行分类实验,图 3显示了真实的地物分布情况。
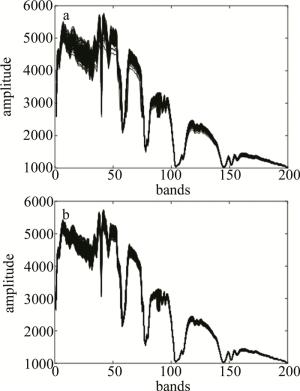
图 4中给出的图像位置为80行50列~90行70列像元的原始谱数据与生成的领域谱数据的比较。其中图 4a为原始数据,图 4b为邻域谱数据(图中波带数和幅值均无单位)。对比两个图可以看出,像元的邻域谱较原始谱具有更好的聚类性,尤其在第40~第100波段之间的数据,明显优于原始的谱特征。
在分类实验中,选择样本数大于400的地物进行训练,因此,参与分类实验的样本共有9种。每一类地物随机选择50个样本作为训练样本,其余作为测试样本进行实验。表 1中给出了4种算法的性能指标。从表 1可知,本文中算法的分类精度与kappa系数明显优于其余几种算法,具有较好的分类性能。
Table 1. Comparison of classification performance of various algorithms on Indian Pines hyperspectral images
PCA SVM SRC CRC proposed method overall accuracy 67.36% 83.72% 76.67% 78.53% 84.62% kappa 0.6552 0.8321 0.7428 0.7752 0.8382 -
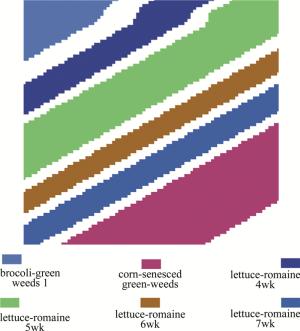
Salinas scene图像大小为512pixel×217pixel,空间分辨率为3.7m,用去掉20个水吸收波段后剩余的204个波段进行实验。本次实验中采用了Salinas scene图像的一个大小为86pixel×83pixel的子图像,其地面真实数据如图 5所示。
数据库2上的分类结果如表 2所示。从表 2可知,在Salinas scene图像上,除了PCA算法,其余4种算法都表现出良好的识别性能,但本文中算法在识别性能与kappa系数上都有一定的优势。
Table 2. Comparison of classification performance of various algorithms on Salinas scene hyperspectral images
PCA SVM SRC CRC proposed method overall accuracy 95.12% 98.26% 97.78% 97.36% 98.82% kappa 0.9431 0.9795 0.9721 0.9712 0.9815 在Indian Pines与Salinas scene数据库上的实验结果表明,随着样本数量与类别数的增加,5种算法的识别性能都有所下降。本文中算法由于充分利用了近邻像元的光谱相似特性,得到的像元光谱特征更稳定,因此获得了更好的识别性能。
-
高光谱图像的空间一致性表明在同一邻域的像元很大概率上属于同类地物的,其光谱数据具有相似性,然而在高光谱数据的生成过程很容易受到由各种因素带影响,容易造成同一邻域同类像元谱特征的差异,为了克服这个困难,本文中通过采用插值方法生成像元的邻域谱,充分利用了高光谱图像空间一致性特点。与原始的谱特征相比较,邻域谱的类内聚类性更好,更利于分类。其次,概率协同表示分类方法是最近提出的一种分类方法,研究表明其具有较高的分类精度。本文中结合邻域谱与概率协同表示分类器,将其应用于高光谱遥感图像的分类中,实验结果表明,所提出的基于邻域谱与概率协同表示方法的高光谱分类方法是一种高性能的分类方法。
邻域谱概率协同表示的高光谱图像分类方法
Hyperspectral image classification method based on neighborhood spectra and probability cooperative representation
-
摘要: 为了提高高光谱遥感图像的分类精度, 通过结合像元邻域谱与概率协同表示方法, 提出了一种基于空间信息与光谱信息的分类方法。首先采用插值方法生成像元的邻域谱, 然后用概率协同表示方法将待测样本进行分类。用所提出的方法在AVIRIS Indian Pines和Salinas scene高光谱遥感数据库上进行分类实验, 并和主成分分析、支持向量机、稀疏表示分类器和协同表示分类器方法进行了比较。结果表明, 所提出的方法在AVIRIS Indian Pines数据库上识别精度比主成分分析法高约17%, 其识别精度和kappa系数都优于另外4种方法。该方法是一种较好的高光谱遥感图像分类方法。Abstract: In order to improve classification accuracy of hyperspectral remote sensing images, a classification method based on spatial information and spectral information was proposed by combining pixel neighborhood spectrum with probability co-representation method. Firstly, the neighborhood spectrum of pixels was generated by interpolation method. Then, the probability cooperative representation method was used to classify the samples to be tested. By using the proposed method, classification experiments were carried out on AVIRIS Indian Pines and Salinas scene hyperspectral remote sensing databases, compared with principal component analysis, support vector machine, sparse representation classifier and cooperative representation classifier. The results show that, the recognition accuracy of the proposed method on AVIRIS Indian Pines database is about 17% higher than that of the principal component analysis method. Its recognition accuracy and kappa coefficient are better than those of the other four methods. This method is a good classification method for hyperspectral remote sensing images.
-
Table 1. Comparison of classification performance of various algorithms on Indian Pines hyperspectral images
PCA SVM SRC CRC proposed method overall accuracy 67.36% 83.72% 76.67% 78.53% 84.62% kappa 0.6552 0.8321 0.7428 0.7752 0.8382 Table 2. Comparison of classification performance of various algorithms on Salinas scene hyperspectral images
PCA SVM SRC CRC proposed method overall accuracy 95.12% 98.26% 97.78% 97.36% 98.82% kappa 0.9431 0.9795 0.9721 0.9712 0.9815 -
[1] DU B, ZHANG Y X, ZHANG L P, et al. A hypothesis in dependent subpixel target detector for hyperspectral images[J]. Signal Process, 2015, 110:244-249. doi: 10.1016/j.sigpro.2014.08.018 [2] WANG Q, YANG G, ZHANG J F, et al. Unsupervised band selection algorithm combined with K-L divergence and mutual information [J]. Laser Technology, 2018, 42(3):417-721 (in Chinese). [3] DALM M, BUXTON M W N, RUITENBEEK F J A. Discriminating ore and waste in a porphyry copper deposit using short-wavelength infrared (SWIR) hyperspectral imagery[J]. Minerals Engineering, 2017, 105:10-18. doi: 10.1016/j.mineng.2016.12.013 [4] KATHRYN E W, SVEIN K S, MARTIN H S, et al. Non-invasive assessment of packaged cod freeze-thaw history by hyperspectral imaging[J]. Journal of Food Engineering, 2017, 205: 64-73. doi: 10.1016/j.jfoodeng.2017.02.025 [5] LUO Sh Zh, WANG Ch, XI X H, et al. Fusion of airborne LiDAR data and hyperspectral imagery for aboveground and belowground forest biomass estimation[J]. Ecological Indicators, 2017, 73:378-387. doi: 10.1016/j.ecolind.2016.10.001 [6] XIA J Sh, FALCO N, BENEDIKTSSON J A, et al. Hyperspectral image classification with rotation random forest via KPCA[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(4):1601-1609. doi: 10.1109/JSTARS.2016.2636877 [7] WANG Y, GUO L, LIANG N. A dimensionality reduction method based on KPCA with optimized sample set for hyperspectral image[J]. Acta Photonica Sinica, 2011, 40(6): 847-851(in Chinese). doi: 10.3788/gzxb [8] CHEONG H P, HAESUN P.A comparison of generalized linear discriminant analysis algorithms [J].Pattern Recognition, 2008, 41(3): 1083-1097. doi: 10.1016/j.patcog.2007.07.022 [9] SMARAJIT B, AMITA P, RITA S, et al. Generalized quadratic discriminant analysis [J]. Pattern Recognition, 2015, 48(8): 2676-2684. doi: 10.1016/j.patcog.2015.02.016 [10] XIANG Y J, YANG G, ZHANG J F, et al. Dimensionality reduction for hyperspectral imagery manifold learning based on spectral gradient angles [J]. Laser Technology, 2017, 41(6): 921-926(in Ch-inese). [11] GU Y F, CHEN W, DI Y, et al. Representative multiple kernel learning for classification in hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(7): 2852-2865 doi: 10.1109/TGRS.2011.2176341 [12] ZHAI Y G, ZHANG L F, WANG N, et al. A modified locality-preserving projection approach for hyperspectral image classification[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(8):1059-1063. doi: 10.1109/LGRS.2016.2564993 [13] HE F, WANG R, YU Q, et al. Feature extraction of hyperspectral image of weighted spatial and spectral locality preserving projectio[J]. Optics and Precision Engineering, 2017, 25(1):263-273(in Chinese). doi: 10.3788/OPE. [14] WRIGHT J, YANG A Y, GANESH A. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2009, 31(2): 210-227. [15] HE Zh, LIU L, ZHOU S H, et al. Learning group-based sparse and low-rank representation for hyperspectral image classification[J]. Pattern Recognition, 2016, 60:1041-1056. doi: 10.1016/j.patcog.2016.04.009 [16] ZHANG E L, ZHANG X R, JIAO L Ch, et al. Weighted multifeature hyperspectral image classification via kernel joint sparse representation [J]. Neurocomputing, 2016, 178:71-86. doi: 10.1016/j.neucom.2015.07.114 [17] ZHANG L, YANG M, FENG X. Sparse representation or collaborative representation: Which helps face recognition?[C]//Proceedings of IEEE International Conference on Computer Vision(ICCV). New York, USA: IEEE, 2011: 471-478. [18] LI J Y, ZHANG H Y, HUANG Y Ch, et al. Hyperspectral image classification by nonlocal joint collaborative representation with a locally adaptive dictionary[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3707-3719. doi: 10.1109/TGRS.2013.2274875 [19] LI W, DU Q. Joint within-class collaborative representation for hyperspectral image classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6):2200-2208. doi: 10.1109/JSTARS.2014.2306956 [20] YUAN M D, FENG D Zh, LIU W J, et al. Collaborative representation discriminant embedding for image classification[J]. Journal of Visual Communication and Image Representation, 2016, 41:212-224. doi: 10.1016/j.jvcir.2016.10.001 [21] ZHANG G Q, SUN H J, XIA G Y, et al. Kernel collaborative re-presentation based dictionary learning and discriminative projection [J]. Neurocomputing, 2016, 207:300-309. doi: 10.1016/j.neucom.2016.04.044 [22] CAI S J, ZHANG L, ZUO W M, et al. A probabilistic collaborative representation based approach for pattern classification[C]//IEEE Conference on Computer Vision and Pattern Recognition. New York, USA: IEEE, 2016: 2950-2959. [23] LI L, GE H W, GAO J Q. A spectral-spatial kernel-based method for hyperspectral imagery classification [J]. Advances in Space Research, 2017, 59(4): 954-967. doi: 10.1016/j.asr.2016.11.006 [24] HOU B H, YAO M L, WANG R, et al. Spatial-spectral semi-supervised local discriminant analysis for hyperspectral image classification[J]. Acta Optica Sinaca, 2017, 37(7):0728002(in Chinese). doi: 10.3788/AOS -


 网站地图
网站地图


 下载:
下载: