-
激光合束的两个特点是:功率高、参与合束的光束波长极其靠近(如光纤激光器波长在1080nm±10nm左右)。激光合束最早在激光核聚变领域提出,如美国NIF计划就是通过192条激光束将2MJ的能量进行合束聚焦,进而引发核聚变[1-5]。光栅是目前常用的合束器件,输出功率主要由窄线宽子束的输出功率和合成路数影响。实用化的光栅合束系统对入射角度十分敏感,因而对装校精度和使用环境要求较高[6-9]。二向色镜光谱合束系统主要是利用大陡度二向色镜将两束红外激光合为一束,最终可获得10kW以上的高能激光输出,具有合束效率高、光束质量好、输出功率大等优点。
虽然二向色镜在普通光束波分复用中是最常见的,高功率激光合束对二向色镜的截止深度、反射率、透过率、反射率曲线陡度等具有很高的要求,过去的技术往往无法满足,二向色镜在光谱合成领域发展较缓。但是随着镀膜技术的提高,二向色镜的性能得到了显著提升,二向色镜合束逐渐成为了继光栅合束后的又一研究内容。二向色镜作为系统的关键器件,其反射性质是影响合束效率的重要因素。因此本研究旨在从二向色镜本身性质出发,通过对二向色镜性能的讨论与改进,达到提高合束效率的目的。
-
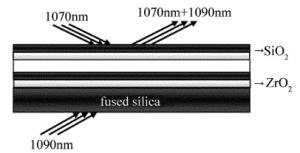
图 1为用于光谱合成的二向色镜,图 2为二向色镜光谱合束原理图。如图 2所示,掺Yb光纤激光器的中心波长分别为1070nm和1090nm,当多模激光束入射至二向色镜表面时,由于二向色镜对1070nm激光具有高反特性,同时对1090nm激光具有高透特性,两路激光经二向色镜后实现光谱合成。
相比于小角度二向色镜,适当增大二向色镜使用角度可以对系统进行结构优化,但这会使二向色镜镀膜难度显著增大,0°的镀制技术相对简单, 但在合束结构上无法实现,45°入射虽然是理论最优的结构,但经过尝试,其镀制结果并不理想。相比之下,小角度二向色镜在使用角度和镀膜光控角度上具有较好的一致性,镀制效果相对理想,是目前合束系统较优的选择。
图 3为多层膜系结构图。假设其有m层膜系,其中第i层膜的折射率为ni,厚度为di,入射介质折射率为n0,基底折射率为ns[10-12]。单个粗糙界面表面面形函数f(x, y)的平均值为0,其几率密度函数呈高斯分布[13-14]。此多层膜系粗糙表面反射模型建立在以下基本假设的基础上:(1)表面粗糙度远小于入射波长;(2)不考虑多层膜系内部及基底的吸收;(3)入射介质和基底假设为半无限大,且基底中不存在反射[15-19]。
假设波长为λ的入射光以小角度θ0入射到多层膜系结构,则入射波电场E0+、反射波电场E0-和透射波电场Es+满足如下关系:
$ \left[ \begin{array}{c}{E_{0}^{+}} \\ {E_{0}^{-}}\end{array}\right]=\boldsymbol{P} \left[ \begin{array}{c}{E_{\mathrm{s}}^{+}} \\ {0}\end{array}\right] $
(1) $ \boldsymbol{P}=\boldsymbol{S}_{01} \boldsymbol{I}_{01} \boldsymbol{T}_{1} \boldsymbol{S}_{12} \boldsymbol{I}_{12} \boldsymbol{T}_{2} \cdots \boldsymbol{T}_{m} \boldsymbol{S}_{m \boldsymbol{S}} \boldsymbol{I}_{m \boldsymbol{S}}=\left[ \begin{array}{ll}{p_{1}} & {p_{3}} \\ {p_{2}} & {p_{4}}\end{array}\right] $
(2) 式中,Sij为第i层和第j层粗糙表面的散射矩阵,Iij为第i层和第j层之间的复振幅传播矩阵,Tj为第j层内部的相位传播矩阵,p1, p2, p3, p4为矩阵元。
$ \boldsymbol{S}_{i j}=\frac{1}{1-r_{i j}^{2}}=\left[ \begin{array}{cc}{a-r_{i j}^{2} b} & {r_{i j}(b-a)} \\ {r_{i j}\left(b^{-1}-a^{-1}\right)} & {a^{-1}-r_{i j}^{2} b^{-1}}\end{array}\right] $
(3) 式中,a和b为与每层厚度、折射率、面形函数相关的光学因子, rij为菲涅耳振幅反射系数。
$ \boldsymbol{I}_{i j}=\frac{1}{t_{i j}} \left[ \begin{array}{cc}{1} & {r_{i j}} \\ {r_{i j}} & {1}\end{array}\right] $
(4) 式中,tij为透射系数。
$ \boldsymbol{T}_{j}=\left[ \begin{array}{cc}{\mathrm{e}^{\mathrm{i} \phi_{j}}} & {0} \\ {0} & {\mathrm{e}^{-\mathrm{i} \phi_{j}}}\end{array}\right] $
(5) 式中,ϕj为第j层的相位厚度。则多层膜系的振幅反射系数为:
$ r=p_{2} / p_{1} $
(6) 反射率为:
$ R=r \cdot r^{*} $
(7) 式中,*表示共轭。合束效率是激光合束效果评价的重要指标之一,高效率的合束装置可以获得更高的输出功率。在合束系统中,入射光通道的光谱展宽是建立光纤激光器与二向色镜耦合效率关系的重要因素[23],因此可在激光光谱的基础上建立以下耦合效率模型:
$ \eta=\frac{\sum\limits_{\lambda_{1}}^{\lambda_{2}}[F(\lambda) R(\lambda)]}{\sum\limits_{\lambda_{1}}^{\lambda_{2}} F(\lambda)} $
(8) 式中,F(λ)为入射光光谱,R(λ)为二向色镜的反射曲线,计算间隔为λ1~λ2。
对于二向色镜合束系统,合束效率则可以表示为:
$\begin{array} [c]{c} \eta=\\ \frac{\sum\limits_{\lambda_{1}}^{\lambda_{2}}\left[F_{1}(\lambda) R(\lambda)\right]+\sum\limits_{\lambda_{1}}^{\lambda_{2}}\left\{F_{2}(\lambda)[1-R(\lambda)]\right\}}{\sum\limits_{\lambda_{1}}^{\lambda_{2}} F_{1}(\lambda)+\sum\limits_{\lambda_{1}}^{\lambda_{2}} F_{2}(\lambda)} \end{array} $
(9) 式中,F1(λ)和F2(λ)分别表示不同中心波长光纤激光器的光谱曲线[5]。可见在光谱曲线已知的情况下,二向色镜的反射率对合束效率具有重要影响。
-
仿真实验所用的大陡度二向色镜采用了基于1/4波长的规整膜系。如图 4所示,以熔融石英(折射率n=1.52)为基底,交替镀制268层ZrO2(n=1.97)及SiO2(n=1.433)膜,并在另一面镀制增透膜。使用TFCalc建立二向色镜多层膜结构模型并进行优化,获得膜系内第i层厚度di,并对每层膜系的面形添加几率密度函数呈高斯分布的随机表面粗糙度。整个膜系结构对1090nm激光有很高的透过率,对1070nm激光有很高的反射率。
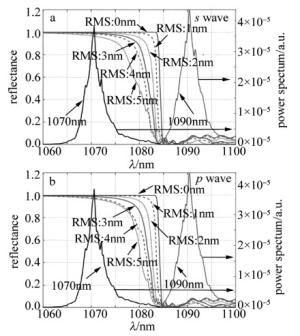
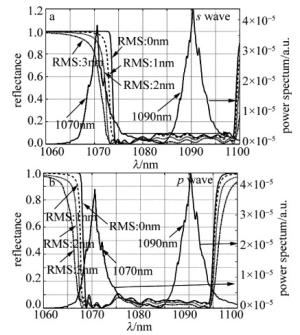
图 5所示为小角度二向色镜反射率仿真曲线与实际测量的激光器光谱曲线,测量波段为1060nm~1100nm。随着表面粗糙度的增加,二向色镜的反射率曲线出现了向短波方向偏移的情况,其原因可能是表面粗糙度的增大使原本镜面反射分量中的一部分变为了散射分量,进而使得同一点的反射率下降。同时,反射率曲线的陡直度也随表面粗糙度的上升发生明显恶化。理想情况下,即当均方根(root mean square, RMS)为0nm时,二向色镜反射率从99.99%降至0.1%的陡直度不到2nm,而当RMS上升到2nm时,这一陡直度更加恶化,反射率从99%降至0.1%的陡直度就已经达到8nm以上,且随着RMS的上升,陡直度将继续下降。结合光谱曲线可知,陡直度的恶化会使接近中心波长处的大量能量损失,因此,光纤激光器的光谱曲线对二向色镜反射率曲线的陡直度提出了要求,根据实际测量的光谱曲线,反射率从99.99%降至0.1%的陡直度应当控制在4nm以内。
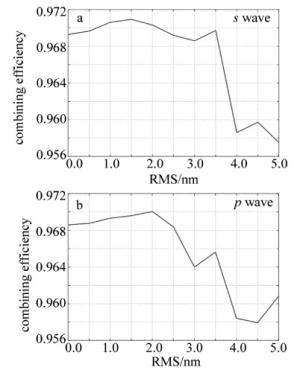
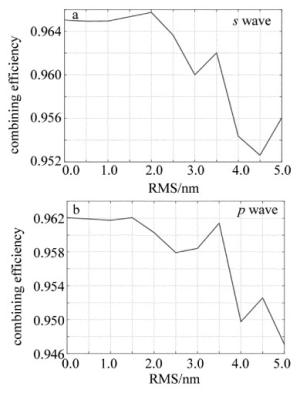
根据光谱曲线与反射率仿真曲线,进一步得到了不同粗糙度下小角度二向色镜的合束效率曲线,如图 6所示。可以看到当RMS小于3.5nm时,合束系统可以获得97%的合束效率,合束效率曲线波动也较为平缓,当二向色镜表面变得更加粗糙,能量损失会使合束效率迅速下降。
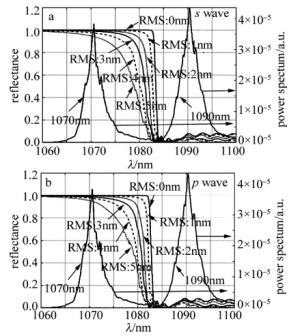
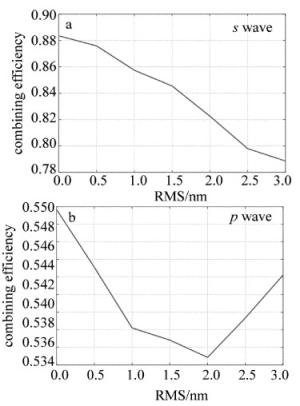
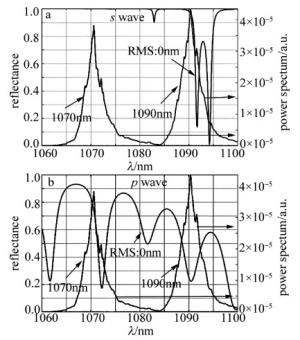
作者对更大角度(5°, 15°和45°)二向色镜也进行了模拟仿真,图 7和图 8为5°二向色镜的仿真结果。可以看出,随着表面粗糙度的增大,二向色镜的反射率曲线均出现了向短波方向漂移的现象,曲线陡直度也发生了明显恶化。相比之前的仿真结果,5°二向色镜的反射率曲线整体更靠近短波方向,为了防止能量损失,5°二向色镜对陡直度提出了更高的要求。且当RMS小于3.5nm时,合束效率浮动依然较为稳定,但合束效率整体下降,最高可获得96%的合束效率,s波与p波的差异也逐渐明显,为了保证合束效率,二向色镜的表面粗糙度要求也需要相应提高。
图 9和图 10为15°二向色镜仿真结果。可以看到, 此时反射率曲线已经完全偏移,中心波长处能量损失极大,且长波方向开始出现另一上升沿。s波与p波差异也更加明显,p波曲线漂移现象更加严重。合束效率也大幅下降,此时s波合束效率最高为88%,p波最高只有55%,已无法满足合束要求。
图 11为RMS为0nm时45°二向色镜的反射率仿真曲线。曲线已经完全变形,无法用于合束。这说明现有的多层膜系粗糙表面反射模型可能已经不适用,大角度二向色镜需要重新建立多层膜系结构,并设计新的镀膜方案。
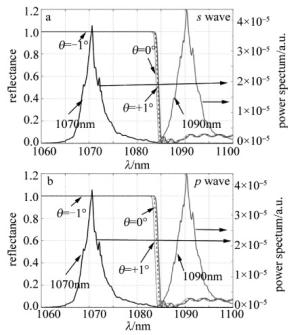
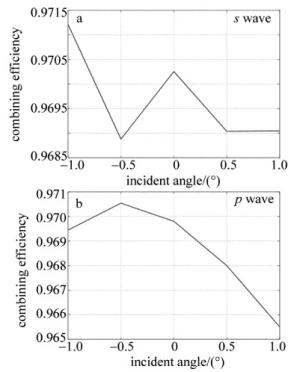
装校误差以及使用过程中的扰动可能会带来入射角度的小幅度改变,因此对小角度二向色镜的稳定性也进行了模拟讨论。如图 12和图 13所示,少量角度误差虽然也会导致反射率曲线的轻微漂移,但曲线陡度基本没有恶化,合束效率的浮动也在0.2%以内。而且实际的人工装校可以将误差控制在1′,因此角度的影响基本可以忽略,可见二向色镜合束系统可以克服角度敏感的问题,在稳定性上具有一定优势。
由上述讨论可见,用于光谱合成的二向色镜对部分关键参量的要求极高,这也对相应的镀膜技术提出了挑战。如使用常用的电子束蒸发技术,则可能需要提高电子束能量,提升膜层致密度。同时提高现有镀膜设备的光控系统精度,例如减少系统中控制片更换次数,使新膜层镀制时不断对之前膜层产生的厚度误差等进行补偿,在一定程度上达到膜层内部互相抵消的效果。更好的方法是使用更加先进的磁控溅射技术,进一步提升镀膜质量。以国内机构的镀制水平,改进后的参量虽然有所提升,如反射率曲线陡度可以得到一定优化,但依然与使用要求存在差距,这也使得目前该二向色镜的来源仍然依赖国外采购。
-
通过建立多层膜系粗糙表面模型,对用于光谱合束的二向色镜的反射率曲线进行了模拟仿真,并合光纤激光器光谱曲线,进一步得到了合束效率仿真结果。可以看出,二向色镜的反射率曲线会随粗糙度的增大向短波漂移,同一点的反射率会下降,反射率曲线陡直度也会恶化,进而降低合束效率。因此在忽略其它因素影响的情况下,若要获得较为理想的合束效果,要在膜层镀制过程中对二向色镜的RMS值以及反射率曲线的陡直度进行控制。
另一方面,适当增大二向色镜的使用角度则对镀膜技术提出了更高的要求,在实际镀制时,需要能够稳定镀制百层以上的高端镀膜机,还需要对光控等进行相应的改造。由于技术难度大、成本高,目前国内关于这方面的研究暂时处于讨论试验阶段。
光谱合束二向色镜反射率及合束效率仿真研究
Simulation of reflectivity and combining efficiency of dichroic mirrors for spectral beam combining
-
摘要: 为了研究合束效率与二向色镜的反射性质之间的关系,通过建立多层膜系粗糙表面反射模型,采用模拟仿真的方法对用于光谱合束的大陡度二向色镜反射率曲线进行了计算分析,结合光纤激光器光谱曲线得到了合束效率的仿真结果。对不同角度二向色镜表面面形与反射率、合束效率的关系进行了分析,对二向色镜合束系统的稳定性进行了模拟讨论,并对二向色镜的部分参量提出了要求。结果表明,使用小角度二向色镜可以获得10kW以上的输出功率,合束效率达97%。这一结果对二向色镜参量的提高是有帮助的。Abstract: In order to study the important relationship between combining efficiency and reflectivity of dichroic mirrors, rough surface reflection model of multilayer coatings was established. Reflective curves of high-steepness dichroic mirrors for spectral beam combining were calculated and analyzed. Simulation results of combining efficiency were obtained by combining the spectral curves of fiber lasers. The relationship between the surface shape of dichroic mirrors with different angles and reflectivity and combining efficiency were analyzed. The stability of the beam combining system based on dichroic mirrors was simulated and discussed. The results show that, output power of more than 10kW can be obtained by using a small angle dichroic mirror, and combining efficiency can reach 97%. This result is helpful for the improvement of the parameters of dichroic mirrors.
-
Key words:
- laser technique /
- spectral beam combining /
- simulation /
- dichroic mirror /
- surface roughness /
- combining efficiency
-
[1] MA Y, YAN H, TIAN F, et al. Common aperture spectral beam combination of fiber lasers with 5kW power high-efficiency and high quality output[J]. High Power Laser and Particle Beams, 2015, 27(4):7-9(in Chinese). [2] MA Y, YAN H, PENG W J, et al. 9.6kW common aperture spectral beam combination system based on multi-channel narrow-linewidth fiber lasers[J]. Chinese Journal of Lasers, 2016, 43(9):0901009(in Chinese). [3] HOU H H, FAN Zh X, SHAO J D, et al. Scalar scattering theory of optical surfaces[J]. Laser & Optoelectronics Progress, 2005, 42(11):35-38(in Chinese). [4] CARNIGLIA C K. Scalar scattering theory for multilayer optical coatings[J]. Optical Engineering, 1979, 18(18):104-115. [5] CHEN F, MA J, ZHU R, et al. Coupling efficiency model for spectral beam combining of high-power fiber lasers calculated from spectrum[J]. Applied Optics, 2017, 56(10):2574. doi: 10.1364/AO.56.002574 [6] CHENG X, WANG J L, LIU Ch H. Beam combining of high energy fiber lasers[J]. Infrared and Laser Engineering, 2018, 47(1):106-116(in Chinese). [7] MA Y, YAN H, SUN Y H, et al. Recent progress of key technologies for spectral beam combining of fiber laser with dual-gratings configuration[J]. Infrared and Laser Engineering, 2018, 47(1):32-45(in Chinese). [8] WANG F, TANG X H, ZHONG L J, et al. Research of beam combination and focusing system of laser diode applied in ceramic welding[J]. Laser Technology, 2018, 42(2):282-288(in Chinese). [9] ZHANG H, SANG Sh B, DUAN Q Q, et al. Research progress of surface roughness of silicon-on-insulator nano-optical waveguide[J]. Laser Technology, 2017, 41(3):367-375(in Chinese). [10] ZHENG Y, YANG Y F, ZHAO X, et al. Research progress on spectral beam combining technology of high-power fiber lasers[J]. Chinese Journal of Lasers, 2017, 44(2):0201002(in Chinese). [11] ZHANG D Y, HAO J P, ZHU Ch, et al. Review on spectral beam combining of fiber lasers[J]. Laser & Infrared, 2016, 46(5):517-521(in Chinese). [12] HAN D F, HU J, NIE Z P. The calculation of scattering for Gaussian rough surface based on stochastic integral equation method[J]. Chinese Journal of Radio Science, 2016, 31(3):457-461(in Chinese). [13] SHEN B Y, ZENG L J, LI L F, et al. Fabrication of polarization independent gratings made on multilayer dielectric thin film substrates[J]. High Power Laser and Particle Beams, 2015, 27(11):79-80(in Chinese). [14] GUO C, KONG M, GAO W, et al. Simultaneous determination of optical constants, thickness, and surface roughness of thin film from spectrophotometric measurements[J]. Optics Letters, 2013, 38(1):40-42. [15] MILOUA R, KEBBAB Z, CHIKER F, et al. Determination of layer thickness and optical constants of thin films by using a modified pattern search method[J]. Optics Letters, 2012, 37(4):449-451. [16] YU Y, WANG W M, LU Y H, et al. Experimental research of spectrally beam combined diode laser based on grating-cavity[J]. Laser Technology, 2010, 34(1):138-140(in Chinese). [17] SCHMIDT O, WIRTH C, NODOP D, et al. Spectral beam combination of fiber amplified ns-pulses by means of interference filters[J]. Optics Express, 2009, 17(25):22974-22982. doi: 10.1364/OE.17.022974 [18] HOU H H, SHEN J, SHEN Z C, et al. Stratified-interface scattering model for multilayer optical coatings[J]. Acta Optica Sinica, 2006, 26(7):1102-1106(in Chinese). [19] HOU H H, SUN X L, SHEN Y M, et al. Roughness and light scattering properties of ZrO2 thin films deposited by electron beam evaporation[J]. Acta Physica Sinica, 2006, 55(6):3124-3127(in Chinese). [20] YU H. Mathematics model analysis of scattering method on measuring surface roughness[J]. Journal of Changchun University of Science and Technology, 2006, 29(1):109-112(in Chinese). [21] TIKHONRAVOV A V, TRUBETSKOV M K, TIKHONRAVOV A A, et al. Effects of interface roughness on the spectral properties of thin films and multilayers[J]. Applied Optics, 2003, 42(25):5140-5148. doi: 10.1364/AO.42.005140 [22] CARNIGLIA C K, JENSEN D G. Single-layer model for surface roughness[J]. Applied Optics, 2002, 41(16):3167-3171. doi: 10.1364/AO.41.003167 [23] BENNETT H E, PORTEUS J O. Relation between surface roughness and specular reflectance at normal incidence[J]. Journal of the Optical Society of America, 1961, 51(2):123-129. doi: 10.1364/JOSA.51.000123 -


 网站地图
网站地图


 下载:
下载: