网站地图
下载:
-
相控阵天线通过调整发射出的微波射频信号相位，最终实现微波射频信号向特定方向射出。相控阵天线结构的核心器件是微波移相器，移相器的要求包括能实现0°~360°的全范围相移，并且保持微波射频信号的功率保持不变、操作带宽足够大、结构简单、成本低、重量轻、体积小。因为传统的电子移相器存在电子瓶颈等缺陷，导致无法满足上述功能，由此微波光子移相器技术得到了快速发展。
微波光子移相器原理大致描述为微波射频信号通过调制器加载到光信号上，再在光域内调整光信号相位，最后对移相后的光信号解调，得到移相后的微波射频信号相位可调。实现微波光子移相器的方法有多种，近年来基于外差混频[1-11]、光纤布喇格光栅(fiber Bragg grating，FBG)[12]、傅里叶域光信号处理器(Fourier-domain optical processor，FD-OP)[13]、快慢光技术[14-15]、矢量技术[16-17]等实现移相的方法都已经被证明。其中目前使用最多的方法是光外差混频法，基于光外差混频法的微波光子移相器是通过控制两个频率不同的光信号的相位差，由光电探测器外差混频后得到相移可控的射频信号实现移相器方案。目前外差混频的方法使用较多的核心器件有双平行马赫-曾德尔调制器(dual-parallel Mach-Zehnder modulator，DPMZM)[1-7]、偏振调制器[8-10]、双偏振正交相移键控制器(dual-polarization quadrature phase shift-keying modulator，DP-QPSK)[11]。前人大多使用各类的马赫-曾德尔调制器，一般包含几个相位调制器(phase mo-dulator，PM)，费用昂贵，器件实现复杂，并且DPMZM存在偏置电压漂移现象。
CHAN等人提出一种基于4个相位调制器和一个光移相器构成的DPMZM的方法实现微波光子移相器，该方案是通过控制载波和边带的相位和幅度来控制射频信号的相位，最终实射频相位0°~360°可调[7]。在本文中, 通过VPI Transmission Maker仿真软件实现的微波光子移相器，相比参考文献[7]中的研究，通过使用一个相位调制器、延时线和光滤波器就能实现射频信号0°~360°可调，在同一输出相位情况下，频率在0GHz~40GHz范围内，功率值保持基本不变。具有结构简单、成本较低等优点，并且相比之前研究[1-7, 11]，相位调制器只需控制一个电压来调节移相角度，而使用复杂DPMZM要调节多个偏置电压，所以利用一个相位调制器减少了使用复杂DPMZM所导致的漂移带来的影响。通过耦合器(optical couple，OC)将激光器(laser device，LD)发出来的激光分成两路:一路信号作为载波经过延时线进行移相，实现载波相位可调; 另一路信号进行相位调制，通过光滤波器滤出上边带，通过控制相位调制器角度来控制边带的相位，实现边带相位可调，再通过另一个耦合器把两条光路结合起来，在光电探测器后输出射频信号(radio frequency，RF)。在实际中带宽受光电探测器(photodetector，PD)和相位调制器带宽限制，在仿真中将频率设置在0GHz~40GHz范围内，发现可实现射频相位0°~360°可调。
-
外差混频法要求两束光信号振动方向相同，频率相差很小，幅度相等并且在同一方向传播，最后通过光电探测器拍频实现相移。两束光信号可分别表示为[18]：
$ \left\{\begin{array}{l}{E_{1}=A \cos \left(\omega_{1} t+\varphi_{1}\right)} \\ {E_{2}=A \cos \left(\omega_{2} t+\varphi_{2}\right)}\end{array}\right. $
(1) 式中，E是电场强度，A是光信号幅值，t是时间，ω是光信号角频率，φ是光信号相位。光信号在光电探测器上进行拍频可得：
$ \begin{array}{c}{E=E_{1}+E_{2}=A\left[\cos \left(\omega_{1} t+\varphi_{1}\right)+\right.} \\ {\cos \left(\omega_{2} t+\varphi_{2}\right) ]}\end{array} $
(2) 由和差化积公式，(2)式可以化简为：
$ \begin{array}{l} E = 2A\cos \left[ {\frac{1}{2}\left( {{\omega _1} + {\omega _2}} \right)t + \frac{1}{2}\left( {{\varphi _1} + {\varphi _2}} \right)} \right] \times \\ \cos \left[ {\frac{1}{2}\left( {{\omega _1} - {\omega _2}} \right)t + \frac{1}{2}\left( {{\varphi _1} - {\varphi _2}} \right)} \right] \end{array} $
(3) 令$\overline{\omega}=\frac{1}{2}\left(\omega_{1}+\omega_{2}\right), \omega_{\mathrm{m}}=\frac{1}{2}\left(\omega_{1}-\omega_{2}\right) $，则(3)式可以简化为：
$ \begin{aligned} E=& 2 A \cos \left[\overline{\omega} t+\frac{1}{2}\left(\varphi_{1}+\varphi_{2}\right)\right] \times \\ & \cos \left[\omega_{\mathrm{m}} t+\frac{1}{2}\left(\varphi_{1}-\varphi_{2}\right)\right] \end{aligned} $
(4) 令$ A_{\mathrm{m}}=2 A \cos \left[\omega_{\mathrm{m}} t+\frac{1}{2}\left(\varphi_{\mathrm{A}}-\varphi_{2}\right)\right]$，则(4)式可以简化为：
$ E=A_{\mathrm{m}} \cos \left[\overline{\omega} t+\frac{1}{2}\left(\varphi_{1}+\varphi_{2}\right)\right] $
(5) 因为两光信号频率相差很小，即${\omega _{\rm{m}}} \ll \bar \omega $，所以把叠加的信号视为载波频率为$ \bar \omega $的调幅波。
因为受到光电探测器的带宽限制，所以在光电探测器上的叠加混频信号只能显示出调制频率${\omega _{\rm{m}}} $，拍频后的光电流为：
$ I \propto A_{\mathrm{m}}^{2}=2 \alpha^{2}\left\{1+\cos \left[2 \omega_{\mathrm{m}} t+\left(\varphi_{1}-\varphi_{2}\right)\right]\right\} $
(6) 式中，α是延时线相位，为常数。把直流分量滤出，则(6)式可以简化为：
$ I_{\omega_{1}-\omega_{2}} \propto \cos \left[\left(\omega_{1}-\omega_{2}\right) t+\left(\varphi_{1}-\varphi_{2}\right)\right] $
(7) 从上述分析可得出，假设两束光信号中心频率满足条件：ω1－ω2=ωRF，光电探测器将两信号拍频后获得频率为ωRF的射频信号，并且通过调整φ1－φ2实现射频信号相移。所以通过调整两束光信号相位的φ1或者φ2，最终控制射频信号相位。
-
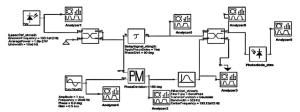
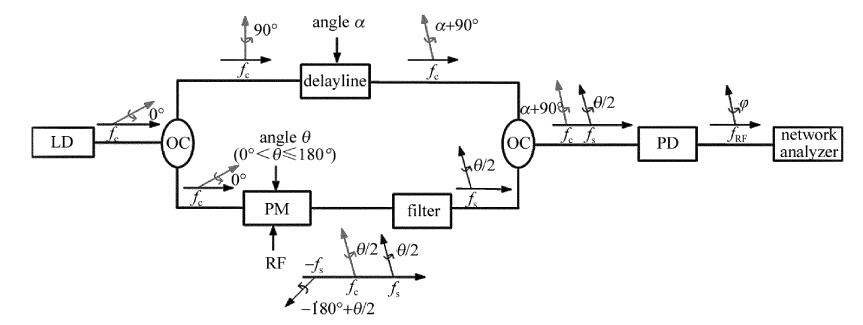
利用上述原理，本文中提出了基于外差混频实现移相器的方案。图 1是移相器的仿真结构图。图中，fc是载波信号频率，fs是边带信号频率，α是延时线相位，θ是相位调制器相位。图 2所示的是在VPI软件中搭建移相器仿真模型。激光器的中心频率为193.1THz，线宽为1MHz，功率为10mW，激光器通过耦合器将信号分成两路，耦合器的一个输出端具有90°相移，将耦合器输出端具有90°相移的信号作为延时线输入信号，通过延时线将载波分别移相0°, 90°, 180°, 270°。这里延时线可以用耦合器、偏振片等无源器件替代，这些无源器件都是能实现相移。激光器通过耦合器输出端未经过移相90°的信号进入到相位调制器中进行相位调制。输入射频信号频率为20GHz，幅度为1V，初始相位为0°，偏置电压为0.5V。通过调整相位调制器的相位范围在0°~180°，再通过3dB带宽的带通滤波器滤出上边带，滤波器中心频率为193.12THz，带宽为5GHz，最后通过另一个耦合器把两路信号进行叠加，把该耦合器未经过相移90°的输出端连接到光电探测器，另一端接地，经过40GHz带宽的光电探测器进行拍频，得到要移相的射频信号。
Figure 1. Schematic diagram of the proposed phase shifter
Figure 2. The simulation model of phase shifter
-
相位调制的光信号的表达式可以化简为[19]:
$ \begin{array}{c}{E_{\mathrm{PM}}=E_{\mathrm{c}}\left\{\mathrm{J}_{0}\left(m_{\varphi}\right) \cos \left(\omega_{0} t\right)+\mathrm{J}_{1}\left(m_{\varphi}\right) \times\right.} \\ {\cos \left[\left(\omega_{0}+\omega^{\prime}\right) t+\frac{\pi}{2}\right]+} \\ {\mathrm{J}_{-1}\left(m_{\varphi}\right) \cos \left[\left(\omega_{0}-\omega^{\prime}\right) t-\frac{\pi}{2}\right] \}}\end{array} $
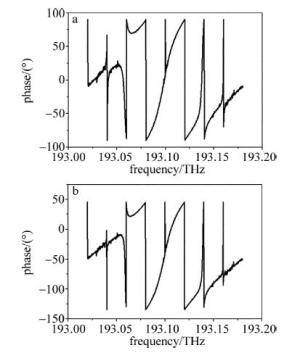
(8) 式中, 后两项分别对应+1阶边带和-1阶边带光场的表达式。Ec为载波信号幅值，t为时间，ω0为光载波信号的角频率，ω′为射频信号的角频率，mφ为调制系数，Jn(mφ)(n=-1，0，1)为贝塞尔函数。如果光电信号直接进入到光电探测器中，由于光电信号的1阶上边带和1阶下边带存在180°相位差，光电探测器无法检测到射频信号。图 3为相位调制后的载波和边带相位谱。如图 3a所示, 当调整相位调制器的相位为180°时，载波相位为90°，+1阶相位为90°，-1阶相位为-90°。如图 3b所示，当相位调制器相位为90°时，载波相位为45°，+1阶相位为45°，-1阶相位为-135°。即当相位调制器的相位θ°(0° < θ≤180°)时，载波相位为θ/2，+1阶相位为θ/2，由于(1阶边带相位差为180°，所以-1阶相位为-180°+θ/2。
Figure 3. Phase spectrum of phase modulator
-
下式对应的是输入射频信号的电场表达式:
$ V_{\text { out }}=V_{\text { bias }}+V_{0} \sin (2 \pi f t+\mu) $
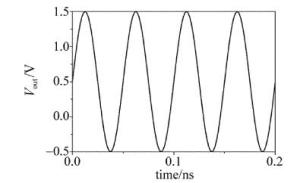
(9) 式中，Vout为输出电压值，Vbias为偏置电压值，E0为输入幅值，f为输入频率，μ为初始相位。仿真中设置V0=1V，初始相位μ=0°，偏置电压Vbias=0.5V，f=20GHz。图 4所示的是在输入射频信号为20GHz情况下输出的时域波形图。周期为0.05ns，当sin(2πft+μ)=0时，输出电压Vout=0.5V，当sin(2πft+μ)=1时，输出电压Vout=1.5V，当sin(2πft+μ)=-1时，输出电压Vout=-0.5V。
Figure 4. Waveform diagram for 20GHz RF signal
图 5所示的是在相位调制器角度为180°、延时线相位为90°的情况下，实现的带通滤波器的高斯1阶滤波器包络及带通滤波器前后的光谱图。图 5a所示的是带通滤波器的高斯1阶滤波器包络；图 5b所示的是滤波器前的光谱图，此时载波的功率为-3.6dBm，±1阶边带功率为-4.2dBm；图 5c所示的是滤波器后的光谱图，此时滤出的是+1阶边带信号，+1阶边带信号功率为-4.2dBm。
Figure 5. a—Gaussian first-order filter envelope of the implemented bandpass filter b—before filtering c—after filtering
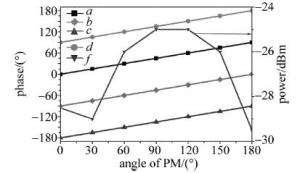
图 6所示的是延时线分别为0°, 90°, 180°, 270°、相位调制器的相位为0°~180°时，输出射频信号的相位和功率谱图。射频信号相位范围分别为0°~90°(a曲线)，-90°~0°(b曲线)，-180°~-90°(c曲线)，90°-180°(d曲线)。移相范围刚好满足0°~360°，功率变化范围均为-30dBm~-25dBm(f曲线)。
Figure 6. Phase and power variation for 20GHz RF signal
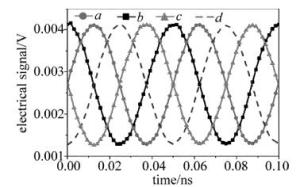
图 7所示的是输入射频信号为20GHz时的射频信号时域图。延时线分别为0°, 90°, 180°, 270°，相位调制器角度为180°时，功率值均为29.5dBm，功率基本保持不变。
Figure 7. Time domain spectrum for 20GHz RF signal
-
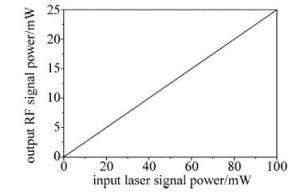
输入扫频信号为0GHz~40GHz，带通滤波器带宽仍为5GHz，滤波器的中心频率随扫频信号频率变化而变化，载波的中心频率fc加上扫频信号的频率fs等于滤波器的中心频率(fc+fs)，其它条件保持不变的情况下，移相器相位谱图和功率谱图如图 8所示。图 8a所示的是移相器扫频相位谱图，通过改变光信号的载波和边带的相位，在保持射频信号功率值不变的情况下，实现射频信号的相位0°~360°可调。图 8b所示为移相器扫频功率谱图，延时线分别为0°, 90°, 180°, 270°、相位调制器角度为180°时，功率值均为29.5dBm，光电探测后射频信号功率保持不变。图 9所示的是激光器输入功率与输出射频信号功率关系。表明当激光器功率为0mW~100mW时，射频信号功率随激光器功率增加呈线性增长状态，射频信号功率范围为0mW~25mW。
Figure 8. The measured phase and amplitude responses of microwave photonic RF phase shifter
Figure 9. The measured output RF signal power versus input laser signal power of microwave photonic RF phase shifter
-
提出了一种新的微波光子移相器，它能实现射频信号相位0°~360°可调，在同一输出相位情况下，频率在0GHz~40GHz范围内，功率值保持基本不变。使用一个相位调制器、延时线和光滤波器来控制载波和边带的相位，最终来控制射频信号的相位。相比之前的研究[1-7, 11]，相位调制器只需控制一个电压来调节移相角度，而使用复杂DPMZM要调节多个偏置电压，所以利用一个相位调制器减少了使用复杂DPMZM所导致的漂移带来的影响。通过使用仿真软件VPI Transmission Maker验证，当延时线相位分别为0°, 90°, 180°, 270°，相位调制器的相位为0°~180°时，所提出的新型微波光子的移相器的范围为0°~360°，射频信号幅度在0GHz~40GHz频率范围内保持不变。
基于载波和边带相位控制的微波光子移相器
Microwave photonic phase shifters based on phase control of optical carrier and sidebands
-
摘要: 为了实现一种360°相移新型微波光子移相器，通过使用一个相位调制器、延迟线和光学滤波器来控制载波和边带的相位，最终控制射频信号的相位。相位调制器只需控制一个电压来调节移相角度，减少了使用复杂双平行马赫-曾德尔调制器所导致的漂移带来的影响，具有结构简单、成本较低等优点。结果表明，仿真验证的微波光子移相器可以在0GHz~40GHz频率范围内实现从0°~360°的全相移范围，并且在同一输出相位情况下，频率在0GHz~40GHz范围内，功率基本保持不变。此研究对微波光子移相器技术有一定参考意义。Abstract: In order to realize a novel microwave photon phase shifter with 360° phase shift, the phase of radio frequency signal was controlled by using a phase modulator, delay line and optical filter to control the phase of carrier and sideband. The phase modulator only needs to control a voltage to adjust the phase shift angle. The effect of drift caused by the use of complex dual-parallel Mach-Zehnder modulator (DPMZM) was reduced. The system had the advantages of simple structure and low cost. The results show that, the microwave photonic phase shifter can achieve full phase shifting from 0°~360° in the frequency range of 0GHz~40GHz. And at the same output phase and under the frequency ranges from 0GHz to 40GHz, the power is basically unchanged. This research has certain reference significance for microwave photonic phase shifter technology.
-
Key words:
- optical communication /
- microwave photonic /
- phase shifter /
- phase modulator
-
Figure 3. Phase spectrum of phase modulator
a—the angle of the phase modulator is 180° b—the angle of the phase modulator is 90°
Figure 5. a—Gaussian first-order filter envelope of the implemented bandpass filter b—before filtering c—after filtering
Figure 8. The measured phase and amplitude responses of microwave photonic RF phase shifter
-
[1] WANG W T, LIU J G, MEI H K, et al. Widely tunable photonic-assisted microwave phase shifter based on single polarization multiplexing electro-optic modulator[J]. IEEE Photonics Journal, 2016, 8(6):1-8. [2] WANG X D, ZHANG J L, CHAN E H W, et al. Ultra-wide bandwidth photonic microwave phase shifter with amplitude control function[J]. Optics Express, 2017, 25(3):2883-2894. doi: 10.1364/OE.25.002883 [3] WANG X, NIU T, CHAN E H W, et al.Photonics-based wideband microwave phase shifter[J]. IEEE Photonics Journal, 2017, 9(3): 5501710. [4] NIU T, WANG X, CHAN E H W, et al. Dual-polarization dual-parallel MZM and optical phase shifter based microwave photonic phase controller[J]. IEEE Photonics Journal, 2016, 8(4):5501114. [5] NIU T, CHAN E H W, WANG X, et al. Broadband dual-polarization dual-parallel Mach-Zehnder modulator based photonic microwave phase shifter[C]//Optoelectronics and Communications Conference. New York, USA: IEEE, 2016: 1-3. [6] LI T, CHAN E H W, WANG X, et al. All-optical photonic microwave phase shifter requiring only a single DC voltage control[J]. IEEE Photonics Journal, 2016, 8(4):5501008. [7] CHAN E H W, ZHNAG W W, MINASIAN R A. Photonic RF phase shifter based on optical carrier and RF modulation sidebands amplitude and phase control[J]. Journal of Lightwave Technology, 2012, 30(23):3672-3678. doi: 10.1109/JLT.2012.2224093 [8] YAO J, LI W, ZHANG W. An ultra wideband 360° photonic assisted microwave phase shifter[C]//Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference. New York, USA: IEEE, 2013: 1-3. [9] WANG W, SUN W, WANG W, et al. A wideband photonic microwave phase shifter using polarization-dependent intensity modulation[J]. Optics Communications, 2015, 356:522-525. doi: 10.1016/j.optcom.2015.08.045 [10] PENG Z, WEN A, GAO Y, et al. A tunable and wideband microwave photonic phase shifter based on dual-polarization modulator[J]. Optics Communications, 2017, 382:377-380. doi: 10.1016/j.optcom.2016.08.006 [11] CHEN Y. A wideband photonic microwave phase shifter with 360 degree phase tunable range based on a DP-QPSK modulator[J]. Optics Communications, 2018, 410:787-792. doi: 10.1016/j.optcom.2017.11.041 [12] ZHAI W Sh, GAO X L, XU W J, et al. Microwave photonic phase shifter with spectral separation processing using a linear chirped fiber Bragg grating[J]. Chinese Optics Letters, 2016, 14(4):16-19. [13] YANG J, CHAN E H W, WANG X, et al. High output RF signal power photonic microwave phase shifter with amplitude and phase control functions[C]//International Conference on Optical Communications and Networks. New York, USA: IEEE, 2015: 1-3. [14] XUE W, SALES S, CAPMANY J, et al. Wideband 360 degrees microwave photonic phase shifter based on slow light in semiconductor optical amplifiers[J]. Optics Express, 2010, 18(6):6156-6163. doi: 10.1364/OE.18.006156 [15] SANCHO J, LLORET J, GASULLA I, et al. Fully tunable 360° microwave photonic phase shifter based on a single semiconductor optical amplifier[J]. Optics Express, 2011, 19(18):17421-17426. doi: 10.1364/OE.19.017421 [16] LOAYSSA A, LAHOZ F J. Broad-band RF photonic phase shifter based on stimulated brillouin scattering and single-sideband modulation[J]. IEEE Photonics Technology Letters, 2005, 18(1):208-210. [17] LI W, ZHU N H, WANG L X. Photonic phase shifter based on wavelength dependence of brillouin frequency shift[J]. IEEE Photonics Technology Letters, 2011, 23(14):1013-1015. doi: 10.1109/LPT.2011.2151279 [18] WANG Ch Y. Photonic microwave phase shifter based on silicon microring[D]. Wuhan: Huazhong University of Science and Technology, 2013: 15-16(in Chinese). [19] XU D. Research on tunable microwave photonic filter based on phase modulation[D]. Tianjin: Tianjing University of Technology, 2017: 20-21(in Chinese). -
点击查看大图
图(9)
计量
- 文章访问数: 3901
- HTML全文浏览量: 2377
- PDF下载量: 16
- 被引次数: 0
