-
板条固体激光器是继棒状固体激光器之后又一种新型固体激光器,它具有光束质量好、输出功率高、偏振态可控、激光放大性能优异和热稳定性好等优点,从发明至今,已得到成功应用,特别是在高功率固体激光系统中[1]。为了满足工程应用对高功率固体激光器长期稳定运转的要求,有必要对激光器的热管理进行更深入的研究[2]。虽然板条固体激光器具有优异的抗热效应能力,在灯抽运和半导体抽运中已得到证明[3-8],但是,如果不对板条固体激光器进行优化设计,其优越性很难发挥。从已有的研究结果来看,对板条固体激光器中激光工作物质的热物理分析,通常是建立在1维无限大的简化处理方法上,即认为板条的宽度远大于厚度,从而可以不考虑板条宽度方向对激光器热物理参量的影响。实际上,一般的板条固体激光介质的宽度与厚度之比并不是无限大,通常板条的长、短边之比小于10。因此,要更精确地描述板条固体激光器,必须考虑板条的短边。只有采用2维处理方式,即建立板条激光器的2维模型,才能得到比较准确的板条激光介质热物理的计算结果。本文中在2维模型下,通过计算板条激光工作物质的温度分布和冷却速率,更精细地说明板条激光器的热特性,以寻求消除固体激光器热效应的有效技术途径,从而实现激光器的有效热管理,达到高功率、高光束质量、高效率和安全稳定工作的精益目标。
-
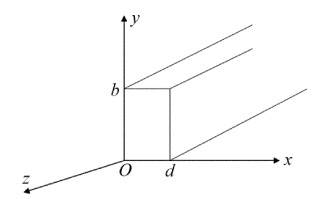
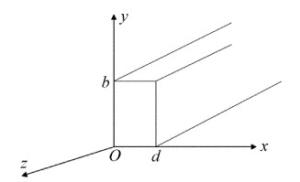
板条固体激光器适合于高功率下运转,且能够克服传统棒状固体激光热效应对激光的光束质量影响,这得益于其中激光工作物质结构设计不同于传统的棒状固体激光器。一般来说,板条激光工作物质是长方体矩形状,如图 1所示。
设板条激光工作介质的厚度为d,宽度为b,长度为L,由于激光沿z轴传输,其前后端面是作为激光输出窗口,不能进行抽运与冷却,所以可以不考虑z轴方向上的激光工作物质的温度变化和端面边界条件,即认为在z方向没有热传导。而且为了克服板条固体激光器的热效应对激光光束质量的影响,通常是在它的x方向进行面抽运和面冷却,并且在它的y方向作绝热处理,形成与y轴对称的温度分布,这样保证在zig-zag光路的均衡下,消除棒状固体激光器无法克服的热-光畸变所导致的激光光束质量下降问题。在理想情况下,可以按1维热分布对板条的温度分布、热应力等物理参量进行计算[5],但是,由于在y方向绝热技术及工艺有差异,更精确的方法是按2维热传导问题对板条激光器进行分析。
当板条激光器的光抽运与冷却处于稳定时,可以认为抽运激励产生的热量和冷却剂散发的热量达到了平衡,这样就可以在稳态下求出2维板条激光工作物质的温度分布。由物理学中的传热学原理论可知,当有内部热源时,2维温度分布T(x, y, t)可以用泊松方程描述[9],即:
$ \frac{\partial^{2} T(x, y)}{\partial x^{2}}+\frac{\partial^{2} T(x, y)}{\partial y^{2}}+\frac{Q}{\kappa}=0 $
(1) 式中,κ是板条激光材料的热导率,Q是抽运光单位时间、单位体积内所产生热量。本文中主要针对稳态运转的激光器,所以注入热量随时间的瞬时变化暂不在考虑范围之中,故Q不考虑时间影响。在如图 1所示的坐标系下,热传导是在激光板条x方向进行且在y方向绝热,设其温度为T0,板条侧面与冷却剂之间的表面传热系数为h,冷却剂温度为Tc。此时,偏微分方程(1)式的边界条件为:
$ \left\{\begin{array}{l}{\kappa \frac{\partial T(x, y)}{\partial x}-h\left.\left[T(x, y)-T_{\mathrm{c}}\right]\right|_{x=0}=0} \\ {\kappa \frac{\partial T(x, y)}{\partial x}+h\left.\left[T(x, y)-T_{\mathrm{c}}\right]\right|_{x=d}=0}\end{array}\right. $
(2) $ T(x, 0)=T(x, b)=T_{0} $
(3) 采用分离变量法求解[10],就可以得到激光工作物质的温度分布为:
$ \begin{array}{c}{T(x, y)=T_{\mathrm{c}}+\frac{Q d}{2 h}+\frac{Q x}{2 \kappa}(d-x)+} \\ {\sum\limits_{n=1}^{\infty}\left\{2 A_{n} \operatorname{ch}\left[\frac{\beta_{n}}{d}\left(y-\frac{b}{2}\right)\right]\right\} \times} \\ {\left[\sin \left(\frac{\beta_{n}}{d} x\right)+\frac{\kappa \beta_{n}}{d h} \cos \left(\frac{\beta_{n}}{d} x\right)\right]}\end{array} $
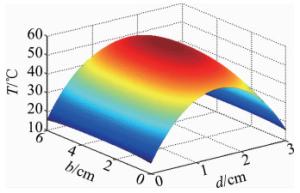
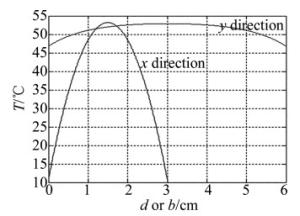
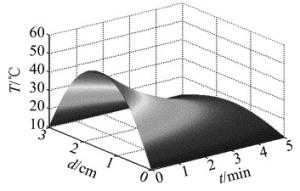
(4) 式中,c是比热容,βn为本征值,可由边界条件(2)式解出,系数An可由边界条件(3)式采用傅里叶级数方法求得。以钕玻璃板条激光器为例[11],钕玻璃板条工作物质尺寸为3cm×6cm×90cm,即d=3cm,b=6cm,钕玻璃热导率κ=1.3×10-2W/(cm·K),如果抽运平均功率为8kW,从而得到相应的热功率Q参量。在x方向,当冷却剂为流动水时,设水的温度为Tc=10℃;当它达到一定的流速通过板条时,传热系数可以达到h=0.1W/(cm2·K)。在y方向,根据板条的绝热方式确定T0的大小,通常T0应低于板条的中心温度,如果取绝热边界温度T0=40℃,根据(4)式和MATLAB软件计算得到的钕玻璃激光板条工作物质内部的温度分布如图 2所示。沿x和y方向中心线的温度分布如图 3所示。从计算结果可知,在2维计算模型下,激光工作物质的温度分布除了沿抽运光方向呈抛物线型分布外,y方向的温度变化呈抛物线型分布。在上述工作条件下,钕玻璃板条激光工作物质的中心最高温度近60℃。为了降低板条的中心温度,可以通过提高散热效率的方式达到,即提高冷却系统的传热系数,如图 4所示。将传热系数提高为h=1.0W/(cm2·K),注入抽运功率等条件不变,板条温度分布的最大值以及两个方向的温度梯度都有一定减小。
-
固体激光器的最大优点之一就是可以工作在高重复脉冲频率下,当重频达到数千赫兹时,其热效应相当于连续工作状态可以采用上述模型方法按稳态处理。但是,中等重频或低重频脉冲固体激光器的热效应在不同的重频下是非稳态的,冷却速率对激光器的热效应有一定的影响。因此, 采用非稳态热传导方程分析激光器的冷却速率是有意义的[12]。
如果忽略沿光传播z轴方向上的温度变化,在图 1所示的坐标系下,由传热学物理中的2维非稳态热传导方程,可以得到板条的温度分布随时间变化所满足的微分方程为[13]:
$ \begin{array}{c}{\frac{\partial T(x, y, t)}{\partial t}=a\left[\frac{\partial^{2} T(x, y, t)}{\partial x^{2}}+\frac{\partial^{2} T(x, y, t)}{\partial y^{2}}\right]} \\ {(0<x<d, 0<y<b, t>0)}\end{array} $
(5) 式中,a是激光板条材料的热扩散率,d为板条的厚度,b为宽度。偏微分方程(5)式的边界条件为:
$ \left\{\begin{array}{l}{\kappa \frac{\partial T(x, y, t)}{\partial x}-h\left.\left[T(x, y, t)-T_{c}\right]\right|_{x=0}=0} \\ {\kappa \frac{\partial T(x, y, t)}{\partial x}+h\left.\left[T(x, y, t)-T_{c}\right]\right|_{x=d}=0} \\ {\left.\frac{\partial T(x, y, t)}{\partial y}\right|_{y=0}=0} \\ {\left.\frac{\partial T(x, y, t)}{\partial y}\right|_{y=b}=0}\end{array}\right. $
(6) 当板条激光器在灯抽运条件和冷却的共同作用下,激光工作物质内部已形成稳定的初始温度分布时,在上述边界条件下求解偏微分方程(5)式,就得到板条激光工作物质的温度分布为:
$ \begin{aligned} T(x, y, t)=T_{\mathrm{c}}+\sum\limits_{m=1}^{\infty} & \sum\limits_{n=1}^{\infty} A_{m n} \exp \left\{-a\left[\left(\frac{\beta_{m}}{d}\right)^{2}+\right.\right.\\ &\left(\frac{n {\rm{ \mathsf{ π} }}}{b}\right)^{2} ] t \}\left[\sin \left(\frac{\beta_{m}}{d} x\right)+\right.\\ & \frac{\kappa \beta_{m}}{d h} \cos \left(\frac{\beta_{m}}{d} x\right) ] \cos \left(\frac{n {\rm{ \mathsf{ π} }}}{b} y\right) \end{aligned} $
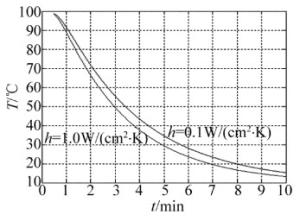
(7) 式中,βm为本征值,可由边界条件(6)式解出,本征值m=0, 1, 2, 3…,系数Amn可由初始条件T(x, y, 0)求得。例如,钕玻璃板条激光工作物质尺寸仍为3cm×6cm×90cm,钕玻璃激光材料的热扩散率a=5.48×10-3cm2/s,如果激光工作物质内部已形成的初始温度分布为T(x, y, 0)=100℃,当冷却水的温度为Tc=10℃、表面传热系数h=0.1W/(cm2·K)时,由(7)式计算得出的2维板条中心温度的冷却速率如图 5所示。图中还给出了其它条件相同但h=1.0W/(cm2·K)的计算结果,结果说明,表面传热系数h的提高,对冷却速率有一定改善,这为激光冷却器的设计提供了一种参考[14]。
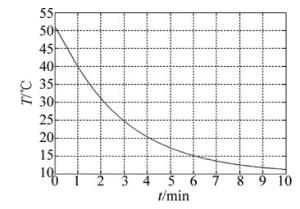
如果激光工作物质内部形成的是如图 2所示的抛物体初始温度分布,即(4)式,当冷却水的温度Tc=10℃、表面传热系数h=1.0W/(cm2·K)时,由(7)式计算得出2维板条中心, 图 6所示就是计算结果,x和y两个方向的温度面分布计算结果如图 7和图 8所示。
-
在目前新的高功率固体激光材料还处于探索攻关阶段的时期,采用现有的固体激光晶体或激光玻璃完成高功率激光输出,仍是一条技术途径[15-17]。所以,通过板条结构攻克固体激光器热效应、提高激光光束质量的研究工作是有实际应用需求背景的。
本文中以2维板条热物理初级模型提供了一种分析板条固体激光器方法热效应的方法,给出了钕玻璃板条激光器温度分布和冷却速率计算结果,为固体激光器的精益化发展注入了新的内容。值得指出的是,本文中虽然是针对灯抽运高功率钕玻璃固体激光器的,推广到二极管抽运板条固体激光器也是顺理成章之事,只是对参量T0的选取,应根据绝热边界条件的实际工艺及测量确定,例如,目前在二极管抽运固体激光器中y方向边界面通常采用铟焊进行冷却,需要在实测和上述理论模型计算下完成优化设计。要解决理论模型与实际器件设计的关系匹配等问题,首先建立测试方法和设备(如热像仪等关键仪器)等技术途径对板条激光器的关键热参量进行绝对值或相对值的测量,可以借鉴热弹性力学或热光学等方法[18-20]。另外,可以进一步分析2维板条的热应力等问题,不难推论:板条固体激光介质的热应力并不是像1维模型的结果或棒状固体激光器那样简单,对热应力的不准确计算将导致实际器件在高功率运转下的灾难性结果,作者将对此作进一步研究。
板条固体激光器的一种热物理模型
A thermphysical model for slab solid-state lasers
-
摘要: 为了获得固体激光器的高功率、高光束质量和高效率,采用理论分析的方法,建立了板条激光介质温度分布和冷却速率等热物理参量的模型,并以灯抽运钕玻璃板条固体激光器为例,进行了数值计算。结果表明,2维模型可以更精确地说明板条固体激光器的温度分布和冷却速率等热物理特征。该研究对高功率板条激光介质的设计具有一定的指导意义。Abstract: In order to obtain high power, high beam quality and high efficiency of solid-state lasers, by means of theoretical analysis, the models of temperature distribution and cooling rate of slab laser mediums were established. A lamp-pumped Nd:glass slab solid-state laser was taken as an example for numerical calculation. The results show that, the temperature distribution and cooling rate of slab solid-state lasers can be more accurately described by the 2-D model. This research has certain guiding significance for the design of high power slab laser mediums.
-
Key words:
- lasers /
- slab laser /
- thermal effect /
- temperature distribution /
- cooling
-
-
[1] MEI S Sh. Advance towards 100kW solid-state lasers[J]. Laser & Optoelectronics Progress, 2005, 42(10):2-8(in Chinese). [2] ZHOU Sh H. The thermal-management in solid-state lasers[J]. Chin-ese Journal of Quantum Electronics, 2005, 22(4):497-509(in Chin-ese). [3] HAN K. The progress of solid-state lasers[J]. Laser Journal, 1983, 4(2):76-80(in Chinese). [4] FANG A P, LOU Q H, DONG J X, et al. Experiment study on the temperature characteristics of LD pumped Nd:YAG laser slab[J]. Chinese Journal of Lasers, 2002, 29(s1):96-98(in Chinese). [5] EGGLESTON J M, KANE T J, KUHN K, et al. The slab geometry laser. Ⅰ-Theory[J]. IEEE Journal of Quantum Electronics, 1984, 20(3):289-301. doi: 10.1109/JQE.1984.1072386 [6] KANE T, ECKARDT R, BYER R. Reduced thermal focusing and birefringence in zig-zag slab geometry crystalline lasers[J]. IEEE Journal of Quantum Electronics, 2003, 19(9):1351-1354. [7] LIU Q, MENG J Q, ZU J F, et al. high repetition frequency narrow pulse electro-optically Q-switched laser for space applications[J]. Chinese Journal of Lasers, 2017, 44(6):0601005(in Chinese). [8] ZHAO G, LI J, PENG X J, et al. Compact repetition diode-pumped slab lasers without thermoelectric coolers[J]. Laser Technology, 2016, 40(5):625-628(in Chinese). [9] CAO Y Zh. Heat transfer[M]. Beijing:Beijing Aviation and Space University Press, 2001:1-21(in Chinese). [10] LIANG K M. The method of mathematic and physics[M]. 3rd ed. Beijing:Higher Education Press, 1998:253-282(in Chinese). [11] HE Sh B, CHEN L, CHEN Y B, et al. Thermal effect of N41 Nd:glass slab with 400mm aperture[J]. Chinese Journal of Lasers, 2017, 44(5):0501007(in Chinese). [12] YANG Sh M, TAO W Q. Heat transfer[M]. 4th ed. Beijing:Higher Education Press, 2006:112-161(in Chinese). [13] KOECHNER W. Solid-state laser engineering[M]. Beijing:Science Press, 2002:171-207(in Chinese). [14] GU Y H. The heat-exchange used in cooling 100W Nd:YAG laser[J]. Laser Technology, 1989, 13(6):44-48(in Chinese). [15] WANG Zh, LIU Y, LIU L, et al. Laser-diode side-pumped Nd:YAG thin slab laser based on MOPA[J]. Laser and Infrared, 2015, 45(4):364-368(in Chinese). [16] ZHANG K, YU D H, HE Y, et al. Analysis on cooling performance of compact mid-infrared solid-state laser[J]. Chinese Journal of Lasers, 2017, 44(3):0301002(in Chinese). [17] HOU J, WANG H X, LIAO D F, et al. Manufacturing process of high-power laser crystals[J]. High Power Laser and Particle Beams, 2014, 26(7):95-99(in Chinese). [18] KANMENSKI A A. Laser crystal[M]. Beijing:Science Press, 1981:66-67(in Chinese). [19] LÜ B D. The laser optics[M]. Chengdu:Sichuan University Press, 1992:191-216(in Chinese). [20] ZHOU Y H, SUN B H. Laser physics[M]. Beijing:Beijing University Press, 1991:68-75(in Chinese). -


 网站地图
网站地图

 下载:
下载: