-
随着激光进入飞秒时代,强激光场与原子、分子相互作用的动力学现象得到了广泛关注[1-4]。高次谐波是超快阿秒动力学的重要发现之一。原子、分子发射谐波的过程可以由LEWENSTEIN或CORKUM提出的半经典模型[5-6]来描述:首先,电子电离进入连续态,形成自由电子(过程A:电离过程);随后,进入连续态的自由电子在激光场中加速并远离核子, 但在激光场反向时,电子又随着激光场反向加速并返回与核子发生碰撞(过程B:加速-回碰过程);最后,辐射出高能光子(过程C:发射谐波过程)。
原子谐波的主要用途之一是用来输出高能量、高强度的稳定单个阿秒脉冲。例如:采用偏振门技术[7-8]、啁啾场调制[9]、多色场控制方案[10-11]、中红外激光场控制方案[12]和空间非均匀场调制方案[13-15]等技术,研究人员获得了一系列超短阿秒脉冲。
分子相比原子具有更多的自由度。近年来激光场与分子的相互作用吸引了更多研究人员的目光,并且发现了一些分子谐波独有的特点,例如:电子与不同原子核碰撞形成的多通道谐波辐射过程[16]、基态与激发态之间的电子跃迁过程[17]等。最近,ZHANG等人[18-19]理论研究了H2+分子谐波辐射的空间分布。结果表明:在引入太赫兹或静态激光场后,负向H核发射谐波的强度得到了增强。
虽然H2+分子谐波辐射的空间分布已经有报道,但都是在空间均匀激光场下的研究。因此,作者引入空间非均匀激光场继续对H2+分子谐波辐射的空间分布进行研究。结果表明:在空间均匀场下,正向H核辐射谐波强度高于负向H核; 在空间非均匀场下,由于金属结构表面出现的等离子共振增强现象,谐波截止能量得到延伸, 并且,负向H核辐射谐波强度明显高于正向H核。随后通过电离几率,电子布局,电子波函数以及谐波辐射的时频分析可以给出H2+分子谐波空间分布的合理解释。最后,通过叠加谐波谱上的谐波,可获得一个脉宽为36as的超短孤立阿秒脉冲。
-
H2+与激光场的相互作用可以通过数值求解核与电子耦合的非玻恩-奥本海默近似含时薛定谔方程来描述[20]:
$ \begin{array}{*{20}{c}} {{\rm{i}}\frac{{\partial \psi \left( {z,R,t} \right)}}{{\partial t}} = \left[ { - \frac{1}{{2{u_{\rm{e}}}}}\frac{{{\partial ^2}}}{{\partial {z^2}}} - \frac{1}{{2{u_{\rm{n}}}}}\frac{{{\partial ^2}}}{{\partial {R^2}}} + V\left( {z,R} \right) + } \right.}\\ {\left. {\left( {1 + \frac{1}{{{m_1} + {m_2} + 1}}} \right)zE\left( {z,t} \right)} \right]\psi \left( {z,R,t} \right)} \end{array} $
(1) 式中,m1,m2是2个核的质量; ue=(m1+m2)/(m1+m2+1)和un=m1m2/(m1+m2)表示电子和核的约化质量; R,z分别为核间距与电子坐标; t为时间,ψ(z, R, t)为波函数。H2+的软核库伦势V(z, R)=(R2+0.03)$ ^{ - \frac{1}{2}} $-$ {\left[ {{{\left( {z - R/2} \right)}^2} + 1.0} \right]^{ - \frac{1}{2}}} $-$ {\left[ {{{\left( {z + R/2} \right)}^2} + 1.0} \right]^{ - \frac{1}{2}}} $。激光场形式为:
$ \begin{array}{*{20}{c}} {E\left( {z,t} \right) = }\\ {E\left[ {1 + sg\left( z \right)} \right]\exp \left[ { - 4\left( {\ln 2} \right){t^2}/{\tau ^2}} \right]\cos \left( {{\omega _1}t} \right)} \end{array} $
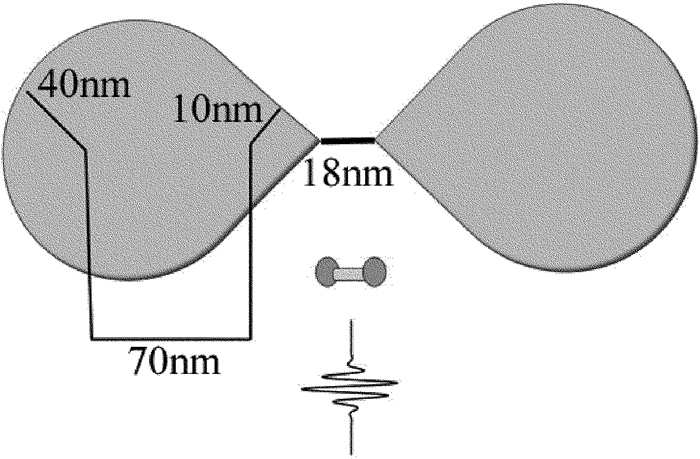
(2) 式中, ω1, E和τ分别为激光场的频率、振幅和脉宽; $ g\left( x \right) = \sum\limits_{i = 1}^N {{\beta _i}{{(x + {z_0})}^i}} $表示空间非均匀形式, βi为空间非均匀参量; s为常数,s=0表示空间均匀激光场, s=1表示空间非均匀激光场; z0表示空间非均匀激光场中心与坐标原点的距离。本文中采用蝴蝶型金属纳米结构,如图 1所示,具体参量可见参考文献[21]。
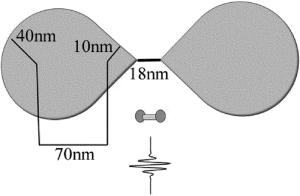
Figure 1. Bowtie-shaped gold nanostructure and geometric parameters[21]
偶极加速度可以表示为[22]:
$ \begin{array}{*{20}{c}} {d\left( t \right) = \left\langle {\psi \left( {z,R,t} \right) \times } \right.}\\ {\left. {\left| { - \frac{{\partial V\left( {z,R} \right)}}{{\partial z}} + \frac{{\partial \left[ {zE\left( {z,t} \right)} \right]}}{{\partial z}}} \right|\psi \left( {z,R,t} \right)} \right\rangle } \end{array} $
(3) $ \begin{array}{*{20}{c}} {d\left( {z < 0.\;0{\rm{a}}{\rm{.}}\;{\rm{u}}{\rm{.}}\;,t} \right) = \int_{ - \infty }^0 {{\psi ^ * }\left( {z,R,t} \right)} \times }\\ {\left\{ { - \frac{{\partial V\left( {z,R} \right)}}{{\partial z}} + \frac{{\partial \left[ {zE\left( {z,t} \right)} \right]}}{{\partial z}}} \right\}\psi \left( {z,R,t} \right){\rm{d}}z} \end{array} $
(4) $ \begin{array}{*{20}{c}} {d\left( {z > 0.\;0{\rm{a}}{\rm{.}}\;{\rm{u}}{\rm{.}}\;,t} \right) = \int_0^\infty {{\psi ^ * }\left( {z,R,t} \right)} \times }\\ {\left\{ { - \frac{{\partial V\left( {z,R} \right)}}{{\partial z}} + \frac{{\partial \left[ {zE\left( {z,t} \right)} \right]}}{{\partial z}}} \right\}\psi \left( {z,R,t} \right){\rm{d}}z} \end{array} $
(5) 式中,上标*表共轭。高次谐波谱图可表示为:
$ S\left( \omega \right) = {\left| {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_0^{{T_{{\rm{total}}}}} {d\left( t \right){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}t} } \right|^2} $
(6) $ \begin{array}{*{20}{c}} {S\left( {z < 0.\;0{\rm{a}}{\rm{.}}\;{\rm{u}}{\rm{.}}\;,\omega } \right) = }\\ {{{\left| {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_0^{{T_{{\rm{total}}}}} {d\left( {z < 0.\;0{\rm{a}}{\rm{.}}\;{\rm{u}}{\rm{.}}\;,t} \right){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}t} } \right|}^2}} \end{array} $
(7) $ \begin{array}{*{20}{c}} {S\left( {z > 0.\;0{\rm{a}}{\rm{.}}\;{\rm{u}}{\rm{.}}\;,\omega } \right) = }\\ {{{\left| {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_0^{{T_{{\rm{total}}}}} {d\left( {z > 0.\;0{\rm{a}}{\rm{.}}\;{\rm{u}}{\rm{.}}\;,t} \right){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}t} } \right|}^2}} \end{array} $
(8) 式中,ω是频率,Ttotal是总传播时间。电离几率和解离几率(解离通道)可以表示为:
$ {P_{\rm{i}}}\left( t \right) = \int_0^t {{\rm{d}}t} \int_0^{R'} {j\left( {R,z',t} \right){\rm{d}}R} $
(9) $ {P_{\rm{d}}}\left( t \right) = \int_0^t {{\rm{d}}t} \int_{ - z'}^{z'} {j\left( {R',z,t} \right){\rm{d}}z} $
(10) $ {P_{ - ,{\rm{d}}}}\left( t \right) = \int_0^t {{\rm{d}}t} \int_{ - z'}^0 {j\left( {R',z,t} \right){\rm{d}}z} $
(11) $ {P_{ + ,{\rm{d}}}}\left( t \right) = \int_0^t {{\rm{d}}t} \int_0^{z'} {j\left( {R',z,t} \right){\rm{d}}z} $
(12) 式中,$j = \frac{1}{m}{\rm{Im}}\left[ {{\psi ^*}{\rm{\delta }} ({s_1} - {s_0})\frac{\partial }{{\partial s}}\psi } \right] $为几率流; R′, z′表示R, z几率流的位置; m表示核质量。当求电离几率时,m=ue, s1=z, s0=z′=25a.u.(本文中a.u.表示原子单位);当求解离几率时,m=un, s1=R, s0=R′=25a.u.。P±, d(t)为电子布局在正(P+, d(t))、负(P-, d(t))向H核的解离通道。这里定义反对称系数A(t)=P-, d(t)-P+, d(t)。当A(t) > 0,表示较多电子布局在负向H核;当A(t) < 0,表示较多电子布局在正向H核;A(t)=0,表示没有解离发生或者电子平均分布在正负向H核。
通过傅里叶变换可获得阿秒脉冲为:
$ I\left( t \right) = {\left| {\sum\limits_q {\left( {\int {d\left( t \right){{\rm{e}}^{ - {\rm{i}}q\omega t}}{\rm{d}}t} } \right){{\rm{e}}^{{\rm{i}}q\omega t}}} } \right|^2} $
(13) 式中,q为谐波次数。
-
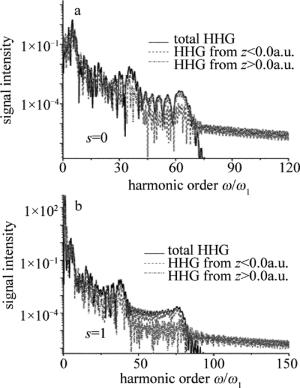
图 2中分别给出H2+在空间均匀(s=0)以及非均匀(s=1)激光场下谐波辐射(high harmonic generation, HHG)的空间分布图(纵坐标信号强度为任意单位)。激光场为5fs/800nm,功率密度I=4.0×1014 W/cm2。由图 2a可知,在空间均匀场下,谐波截止频率为68ω1,其对应的截止能量与经典预言值Ecutoff=I′+3.17U′一致。其中,I′是H2+的电离势,U′为自由电子的有质动力势。并且,正向H核辐射谐波强度高于负向H核。由图 2b可知,随着空间非均匀场引入,金属结构表面出现等离子共振增强现象[13],谐波截止能量得到延伸,并且负向H核辐射谐波强度明显增强。
图 3中给出H2+在空间非均匀激光场(s=1)下发射谐波的特点。空间非均匀激光场位置分别为z0=-100a.u.,z0=-60.0a.u.,z0=60a.u.,z0=100a.u.。这里只给出4个z0下的谐波光谱。由图 3可知,随着空间非均匀激光场引入位置由负向到正向移动(z0=-100a.u.~100a.u.),谐波的有效截止能量得到进一步延伸。尤其当z0=100a.u.时,谐波截止频率为150ω1,对应的截止能量为I′+2.7×3.17U′,相当于激光强度增强了2.7个数量级。从图 3可知,当z0为负值时,第二平台区的谐波强度比第一平台区低2~3个数量级,这不利于实验的观察和获得。因此,定义当z0为负值时,第一平台区截止能量为有效谐波截止频率。负向H核辐射谐波强度依然要比正向H核辐射谐波强度高。
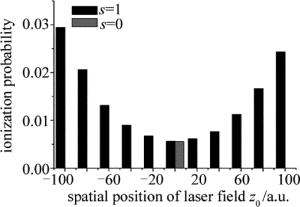
图 4中给出H2+在空间均匀(s=0)以及非均匀场(s=1)下的电离几率。由图可知,随着空间非均匀效应的引入,H2+分子电离几率被增大,因此导致谐波截止能量延伸。在空间非均匀激光场下,激光场在负向z0时比正向z0时电离几率大,即呈现反对称的特点。YAVUZ等人[15]研究表明,当z0为负值时,电子倾向于朝着纳米金属表面移动,因此增大了电离几率。但是在某一特殊位置时,电子到达了金属表面并且被吸收,因此导致谐波有效截止能量减小。反之,当z0为正值时,电子倾向于沿着路径返回,因此导致与母核回碰几率增大,进而导致谐波截止能量延伸。
图 5是H2+在空间均匀与非均匀激光场下不同H核发射谐波的时频图分析图[23]。横坐标中T表示800nm激光场的光学周期。从图中可知,谐波光谱主要有3个谐波辐射过程(P1,P2,P3)。在空间均匀场下(见图 5a和图 5b),谐波辐射过程P2在正向H核的强度要大于负向H核。在空间非均匀场下(图 5c~图 5h分别对应于z0为-100a.u.;0.0a.u.;100a.u.),谐波辐射过程P2在负向H核的强度要大于正向H核,因此导致了谐波反对称空间分布。而且,随着空间非均匀效应的引入,谐波辐射过程的最大能量被延伸了。具体来说,当z0=-100a.u.时,谐波辐射过程P1的能量被延伸,但是其辐射强度很低;当z0=100a.u.时,谐波辐射过程P2的能量被延伸,并且强度与其它2个辐射过程相当,因此导致了图 2和图 3所示的谐波谱图特点。
图 6是空间均匀(s=0)和非均匀(s=1, z0=0.0a.u.)激光场结束后的电子波包演化图。由图可知,在空间均匀场下,电子有较大几率布局在正向H核附近;相反,在空间非均匀场下,电子更倾向于布局在负向H核附近。由“三步模型”可知,谐波辐射过程由电子与母核的回碰过程产生,因此,具有较大电子布局的核会产生更强的谐波辐射,这就是图 2和图 3所示H2+谐波空间反对称分布的根本原因。
图 7a中给出H2+在空间均匀(s=0)和非均匀场(s=1, z0=0.0a.u.)下的总解离几率和正负向H核解离通道大小。由图可知,在空间均匀场下,正向H核解离通道大于负向H核,反对称系数A=-1.92×10-2,说明电子倾向于布局在正向H核;随着空间非均匀参量引入,总解离几率Pd有微小增大,但是,正向H核解离通道小于负向H核,反对称系数A=1.97×10-2,表明电子有较大几率布局在负向H核,这与图 2谐波空间反对称分布和图 6电子波函数分析一致。图 7b中给出空间非均匀场下空间位置z0对于解离几率的影响。由图可知,随着z0由负向到正向移动,总解离几率和正负向H核解离通道都呈现M形分布,最大解离发生在z0=±40a.u.处。当|z0| > 40a.u.时,解离几率减小。这是因为当激光空间位置远离坐标原点后,例如:|z0| > 40a.u.,金属表面等离子共振增强非常明显,导致激光强度非线性增大[13],因此导致电子有较大几率发生电离(见图 4中的电离几率),从而抑制了解离的发生。图 7c中给出反对称系数A随激光场空间位置z0的变化。从图中可知,所有的反对称系数A都大于0,表明电子布局在负向H核的几率大。随着z0由负向到正向移动,反对称系数也呈现类似的M形分布,最大值A=2.2×10-2出现在z0=40a.u.处。
上述分析可知,激光场对分子谐波空间分布有较大影响,分子谐波呈反对称分布。虽然实验上目前较难区分谐波具体产生于哪个核子,但是,YAVUZ等人[15]理论研究表明,空间均匀场与非均匀场下H2+分子的反对称系数呈异号分布,这与作者的理论计算结果一致,可以间接证明本文中计算结果的正确性。
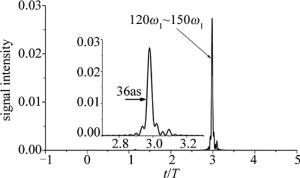
由图 3可知,谐波截止能量在激光空间位置z0=100a.u.时可以得到明显延伸。因此,选用z0=0.0a.u.时的谐波作为输出阿秒脉冲的条件。由图 5g和图 5h分析可知,每一个谐波辐射过程都有长短两条量子路径贡献产生,这不利于单个阿秒脉冲的产生[24]。但是当谐波大于80ω1时,只有单独的P2过程对谐波能量起作用,并且随着谐波能量趋于截止处,长短量子路径合并成1条路径,这有利于单个阿秒脉冲的输出。因此,通过叠加谐波截止能量附近的120ω1~150ω1次谐波,可获得1个36as的超短孤立阿秒脉冲,如图 8所示。
-
本文中理论研究了H2+分子在空间均匀及非均匀激光场下的谐波空间分布情况。计算结果表明:在空间均匀场下,正向H核辐射谐波强度高于负向H核。在空间非均匀场下,负向H核辐射谐波强度明显高于正向H核。并且由于在金属结构表面出现的等离子共振增强现象,谐波截止能量得到延伸。随后通过分析电离几率、电子布局、电子波函数以及谐波辐射的时频可以给出H2+分子谐波空间分布的合理解释。通过适当叠加谐波,可获得脉宽为36as的脉冲。
非常感谢大连化物所韩克利研究员以及南京理工大学陆瑞峰教授所提供的计算程序。
空间均匀和非均匀场下H2+辐射谐波的空间分布
Spatial distribution of H2+ radiation harmonics in spatial homogeneous and inhomogeneous fields
-
摘要: 为了了解H2+分子辐射谐波的空间分布,采用数值求解非玻恩-奥本海默近似的薛定谔方程,进行了空间均匀和非均匀激光场下H2+分子谐波辐射的空间分布研究。结果表明,在空间均匀场下,正向H核辐射谐波强度高于负向H核;在空间非均匀场下,由于金属结构表面出现的等离子共振增强现象,谐波截止能量得到延伸;负向H核辐射谐波强度明显高于正向H核,随后通过电离几率、电子布局、电子波函数以及谐波辐射的时频分析可以给出H2+分子谐波空间分布的合理解释。通过叠加谐波谱上的谐波,可获得一个脉宽为36as的超短孤立阿秒脉冲。该研究对分子谐波的空间分布及阿秒脉冲的输出是有帮助的。Abstract: In order to understand spatial distribution of H2+ molecular harmonics, the spatial distribution of H2+ molecular harmonic spectra in spatial homogeneous and inhomogeneous fields was studied through solving non-Bohn-Oppenheimer time-dependent Schr dinger equation. The results show that in spatial homogeneous field, harmonic intensity from positive-H nucleus is higher than that from negative-H nucleus. In spatial inhomogeneous field, due to plasma resonance on metallic nanostructure surface, harmonic cutoff is extended, and harmonic intensity from negative-H nucleus is higher than that from positive-H nucleus. Furthermore, spatial distribution of the harmonics can be explained by ionization probability, electron localization in two nuclei, time-dependent wave function and time-frequency analyses of harmonic spectra. Finally, by superposing a selected harmonics properly, an isolated ultrashort 36as pulse can be obtained. The investigation is helpful for understanding spatial distribution of molecular harmonics and producing attosecond pulses.
-
Figure 1. Bowtie-shaped gold nanostructure and geometric parameters[21]
-
[1] WANG C, LIU H L, TIAN J S, et al. Analysis of intrinsic atomic phase in process of extreme ultraviolet attosecond pulse generation[J]. Laser Technology, 2012, 36(3): 342-345 (in Chinese). [2] WANG C, KANG Y F, TIAN J S, et al. Analysis of phase dependence of the two single-attosecond-pulse generation techniques[J]. Laser Technology, 2012, 36(4): 516-519 (in Chinese). [3] UIBERACKER M, UPHUES T, SCHULTZE M, et al. Attosecond real-time observation of electron tunnelling in atoms[J]. Nature, 2007, 446(7136): 627-632. doi: 10.1038/nature05648 [4] GOULIELMAKIS E, SCHULTZE M, HOFSTETTER M, et al. Single-cycle nonlinear optics[J]. Science, 2008, 320(5883): 1614-1617. doi: 10.1126/science.1157846 [5] LEWENSTEIN M, BALCOU P, IVANOV M Y, et al. Theory of high-harmonic generation by low-frequency laser fields[J]. Physical Review, 1994, A49(3): 2117-2132. [6] CORKUM P B. Plasma perspective on strong field multiphoton ionization [J]. Physical Review Letters, 1993, 71(13): 1994-1997. doi: 10.1103/PhysRevLett.71.1994 [7] SANSONE G, BENEDETTI E, CALEGARI F, et al. Isolated single-cycle attosecond pulses[J]. Science, 2006, 314(5798): 443-446. doi: 10.1126/science.1132838 [8] CHANG Z H. Chirp of the single attosecond pulse generated by a polarization gating[J]. Physical Review, 2005, A71(2): 023813. [9] FENG L Q, CHU T S. Generation of an isolated sub-40as pulse using two-color laser pulses: Combined chirp effects[J]. Physical Review, 2011, A84(5): 053853. [10] ZENG Z, CHENG Y, SONG X, et al. Generation of an extreme ultraviolet super continuum in a two-color laser field[J]. Physical Review Letters, 2007, 98(20): 203901. doi: 10.1103/PhysRevLett.98.203901 [11] LU R F, HE H X, GUO Y H, et al. Theoretical study of single attosecond pulse generation with a three-colour laser field[J]. Journal of Physics, 2009, B42(22): 225601. [12] LI P C, LAUGHLIN C, CHU S I. Generation of isolated sub-20-attosecond pulses from He atoms by two-color midinfrared laser fields[J]. Physical Review, 2014, A89(2): 023431. [13] KIM S, JIN J, KIM Y J, et al. High-harmonic generation by resonant plasmon field enhancement[J]. Nature, 2008, 453(7196): 757-760. doi: 10.1038/nature07012 [14] SHAARAN T, CIAPPINA M F, LEWENSTEIN M. Quantum-orbit analysis of high-order-harmonic generation by resonant plasmon field enhancement[J]. Physical Review, 2012, A86(2): 023408. [15] YAVUZ I, CIAPPINA M F, CHACÓN A, et al. Controlling electron localization in H2+ by intense plasmon-enhanced laser fields[J]. Physical Review, 2016, A93(3): 033404. [16] FENG L Q, LIU H. Theoretical investigation of the asymmetric molecular harmonic emission and the attosecond pulse generation[J]. Journal of Molecular Modeling, 2015, 21(3): 1-9. [17] BIAN X B, BANDRAUK A D. Multichannel molecular high-order harmonic generation from asymmetric diatomic molecules[J]. Physical Review Letters, 2010, 105(9): 093903. [18] ZHANG J, GE X L, WANG T, et al. Spatial distribution on high-order-harmonic generation of an H2+ molecule in intense laser fields[J]. Physical Review, 2015, A92(1): 013418. [19] ZHANG J, PAN X F, XIA C L, et al. Asymmetric spatial distribution in the high-order harmonic generation of a H2+ molecule controlled by the combination of a mid-infrared laser pulse and a terahertz field[J]. Laser Physical Letters, 2016, 13(7): 075302. doi: 10.1088/1612-2011/13/7/075302 [20] LU R F, ZHANG P Y, HAN K L. Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields[J]. Physical Review, 2008, E77(6): 066701. [21] XUE S, DU H C, XIA Y, et al. Generation of isolated attosecond pulses in bowtie-shaped nanostructure with three-color spatially inhomogeneous fields[J]. Chinese Physics, 2015, B24(5): 054210. [22] BURNETT K, REED V C, COOPER J, et al. Calculation of the background emitted during high-harmonic generation[J]. Physical Review, 1992, A45(5): 3347-3349. [23] ANTOINE P, PIRAUX B, MAQUET A. Time profile of harmonics generated by a single atom in a strong electromagnetic field[J]. Physical Review, 1995, A51(3):R1750-R1753. [24] MAIRESSE Y, BOHAN A D, FRASINSKI L J, et al. Attosecond synchronization of high-harmonic soft X-rays[J]. Science, 2003, 302(5650): 1540-1543. doi: 10.1126/science.1090277 -


 网站地图
网站地图

 下载:
下载: